《Pytorch Tutorial》Notes(初稿)
《Pytorch Tutorial》Notes(初稿)
2024-03-31~04-02 @isSeymour
[TOC]
01、Overview
1.1 引入
-
预测与推理
1.2 分类与历史
-
scikit-learn
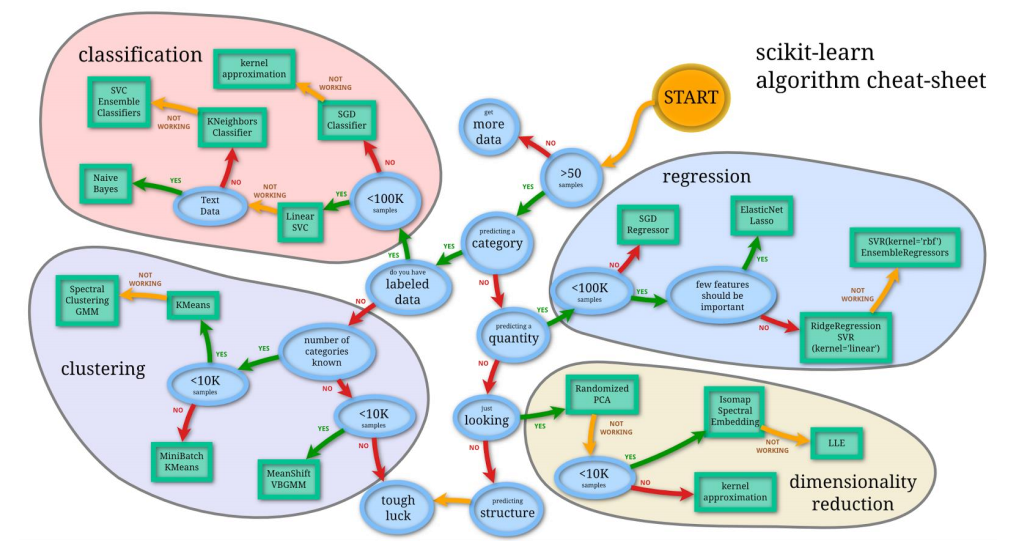
-
历史
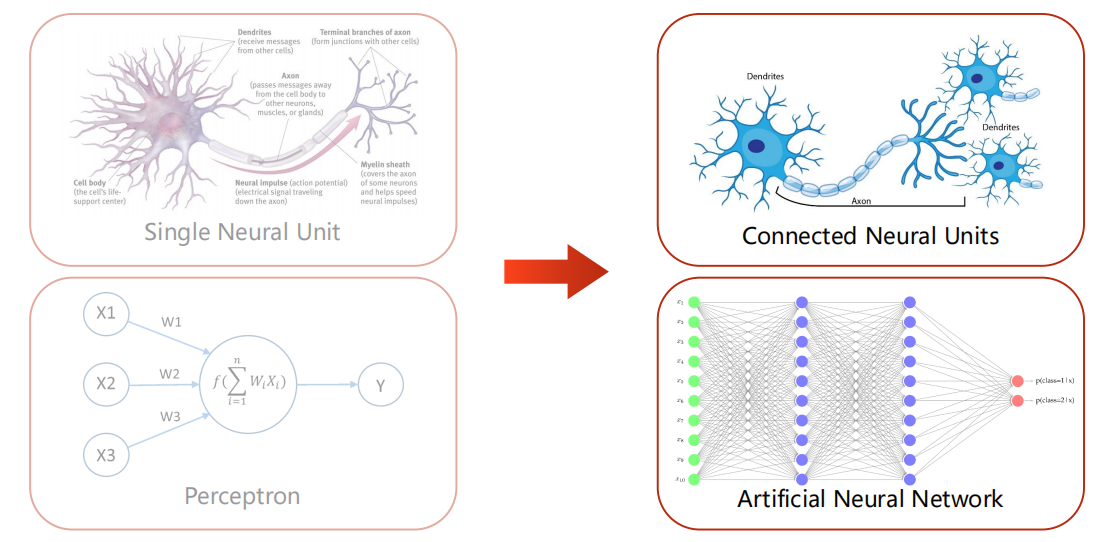
-
思考:降维
思考:降维的意义与原理
意义
意义:根据大数定律,当数据量足够大时,样本数据频率就能基本代表真实分布。
因此,我们希望能在有限但足够的数据量下,完成这个目标。
我们假设每一个特征,需要10个数据量,才能达到大数定律的要求。
那么当特征是两个(二维)时,那么将需要 10^2^ 个才能同时使得二维特征都达到大数定律要求;
若三维,则需要 10^3^ 个数据量;
以此类推,所需数据量将爆炸!——这就是“维度诅咒”。
因此,降维迫在眉睫,降维才能使得有限的数据量更加有效地反应真实分布。
原理
原理:
假设有10个数据量,每个数据量都是n维特征量,而我们希望降维到三维。
实际上,就是将一个 的矩阵,希望线性变换到 的矩阵。
那么我们只需要找到一个变换矩阵 就能完成变换了。
深入:
- 这个线性变换是不是使部分数据损失了?若损失了,为什么能这么做?
- 换句话说,线性变换是在降维,那么这种降维到底是在做什么,能使得降维既可以突破维度诅咒,又能有效代替原维度?
我的思考:
首先,肯定是有数据损失了。
我们通过具体看这个降维的矩阵变换,你会发现,(按照上例),是三次线性结合,每次线性结合是把一个数据量的n个特征都凝聚到一个特征里面,而此次线性结合每个特征的权值,就是矩阵 做的事情了。
所以说,你可以认为,降维实际上是在做两件事情:
找有效特征间的联系:
通过权值,把各个特征量区别性地凝聚为一个。
若一次凝聚不够,就多次凝聚。
(上例是3次,但是不可过多,比如n次,那相当于原特征量乘了单位矩阵)
丢弃掉无效特征:
无效特征量,若是占用一整个维度,这既不合理,且妨碍计算。
因此无效数据量在矩阵 中会出现 即将不再影响数据性质。
(丢弃无效特征,本质上也是一种寻找特征间联系,这个联系是无联系)
反思
从这里你可以看到,降维的难点在哪?
- 如何确定维度
- 如何寻找高效的变换矩阵
-
前馈与反向传播
-
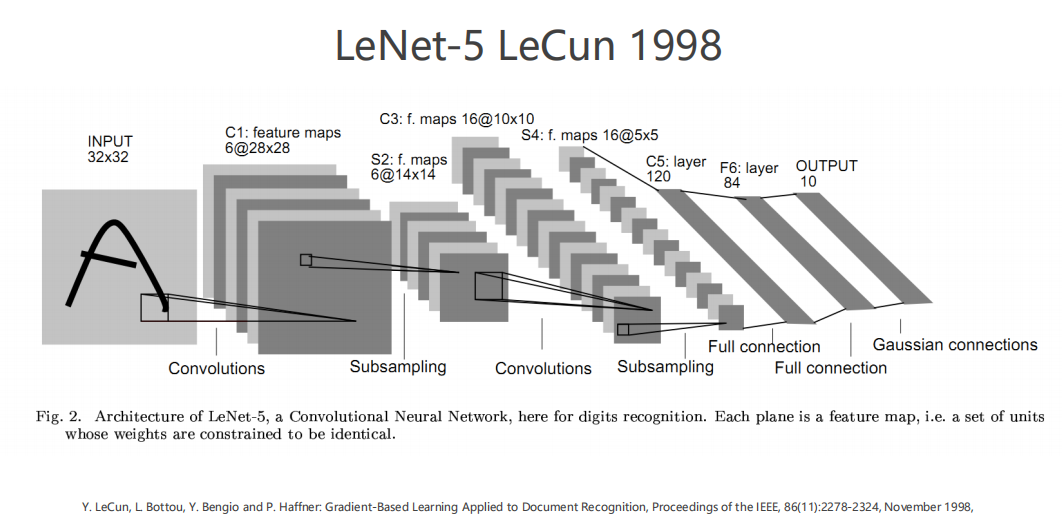
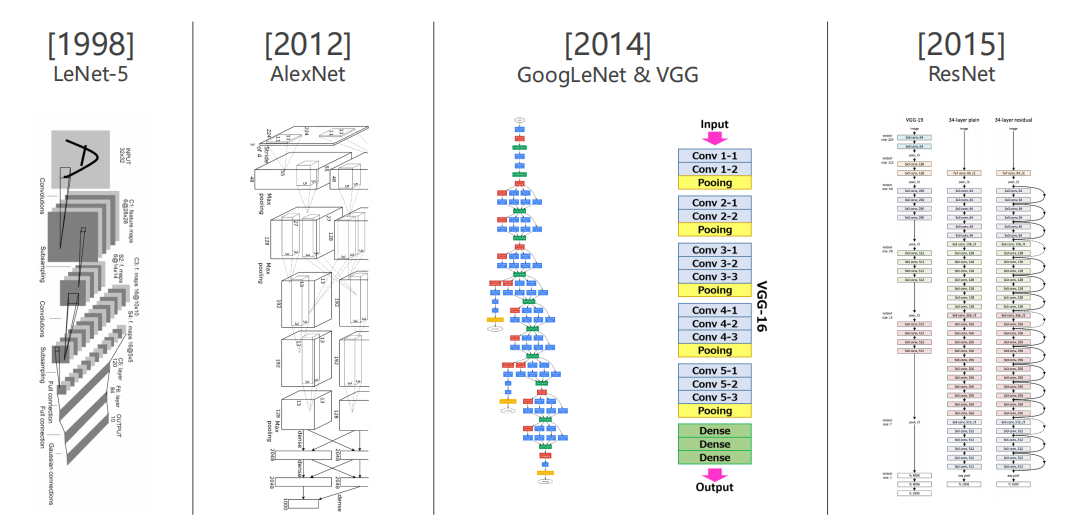
一些模型
1.3 开始吧
参考其他链接,安装好 Pytorch 和 cuda
1 | import torch |
02、Linear Model
2.1 引入

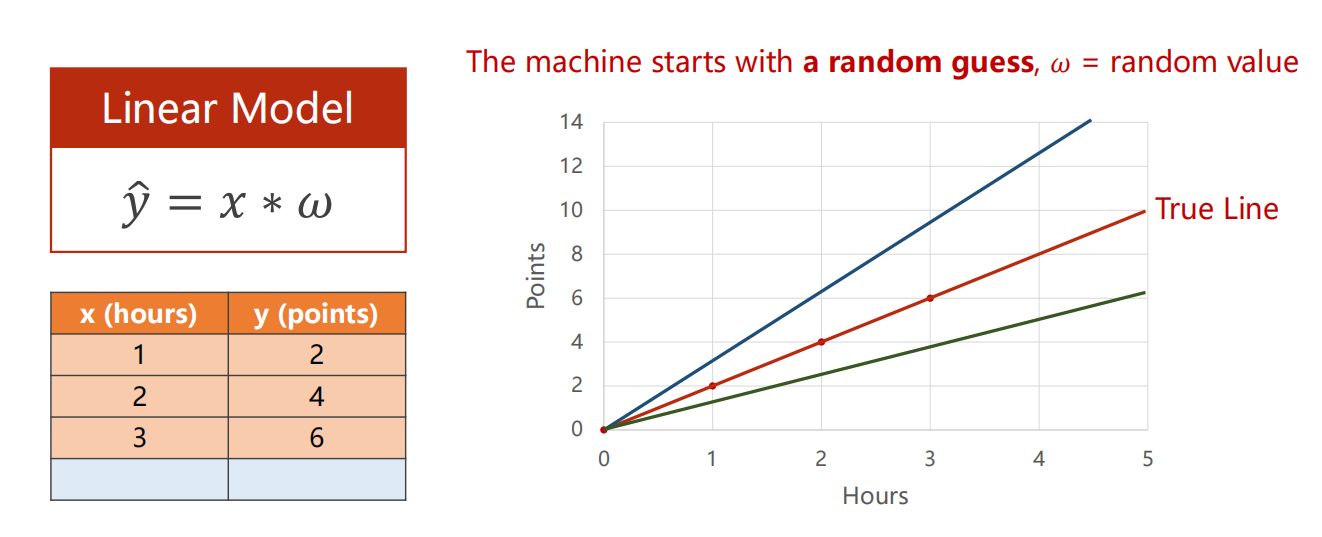
2.2 损失函数
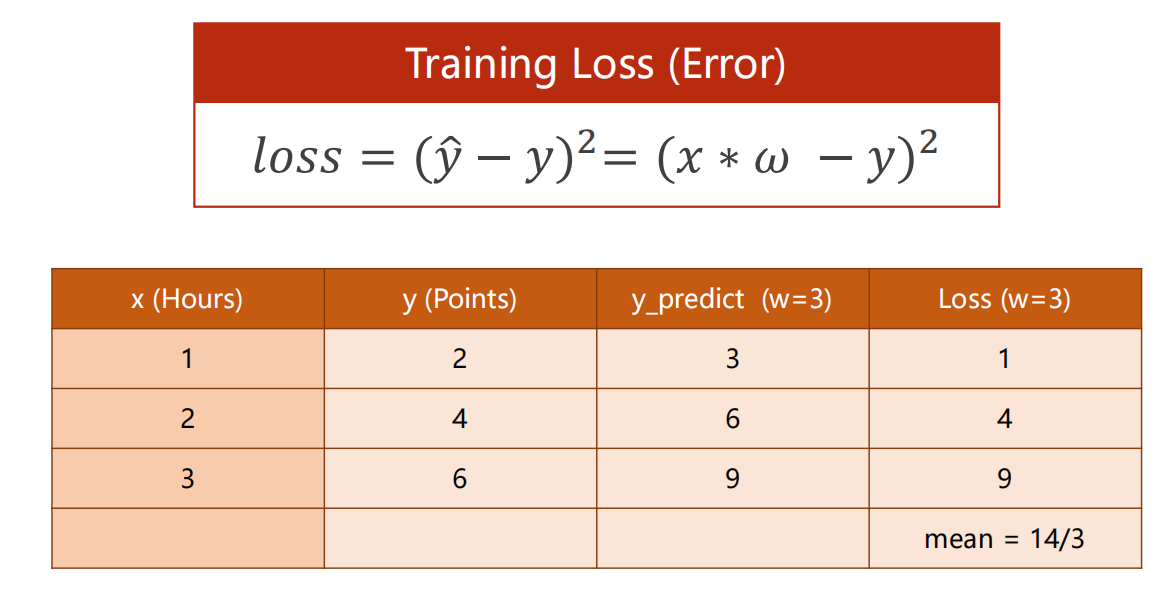
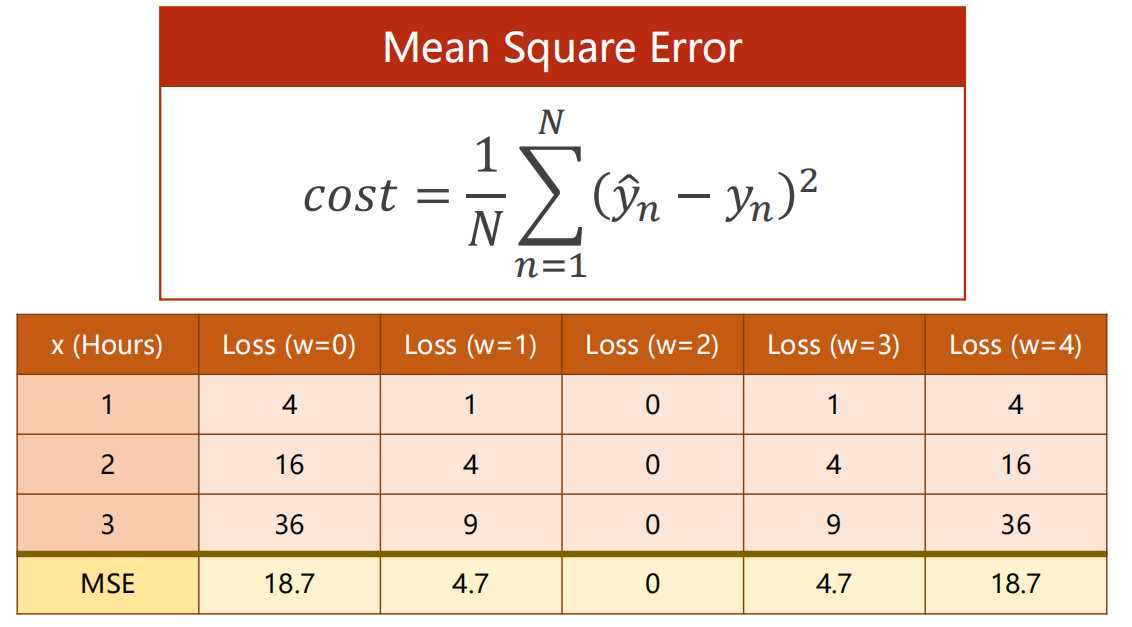
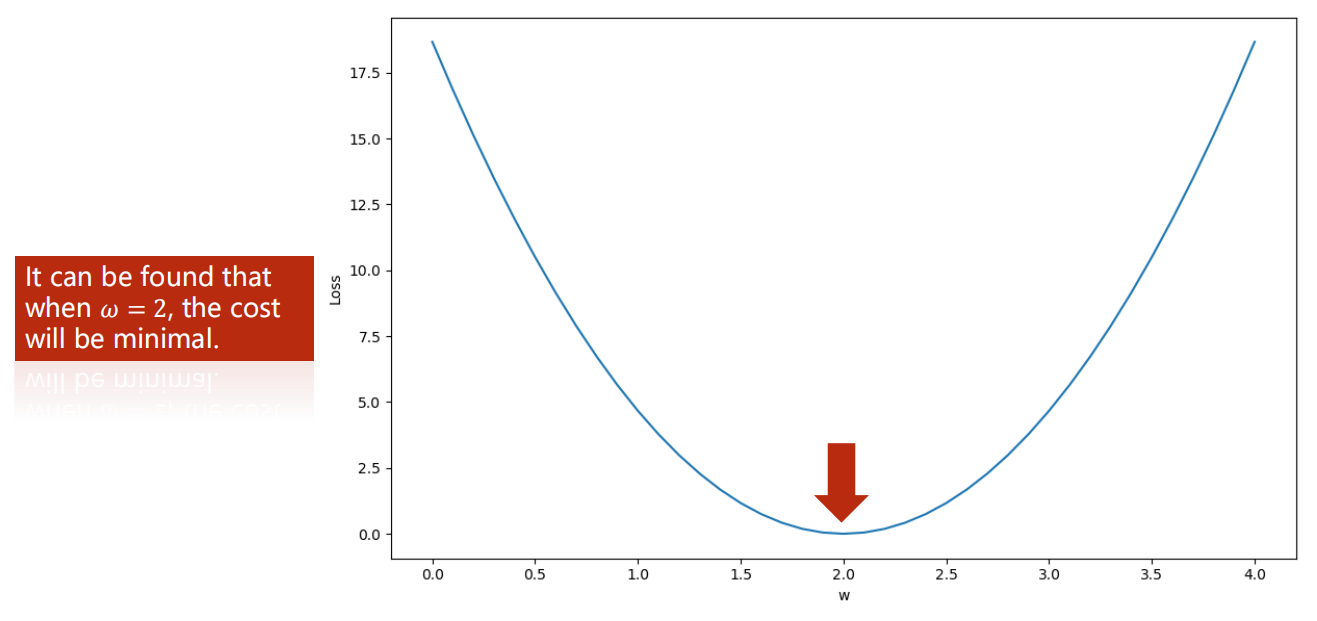
对于线性模型
我们实际上就是想找到一个合适的 使得模型尽可能的去拟合数据
(即,模型输入 预测出的 ,很接近真实的 )
这么多数据,我们怎么评判哪个 是最好的?
因此,需要制定一个标准来从数学数值上进行量化判定,损失函数 应运而生。
2.3 代码实现
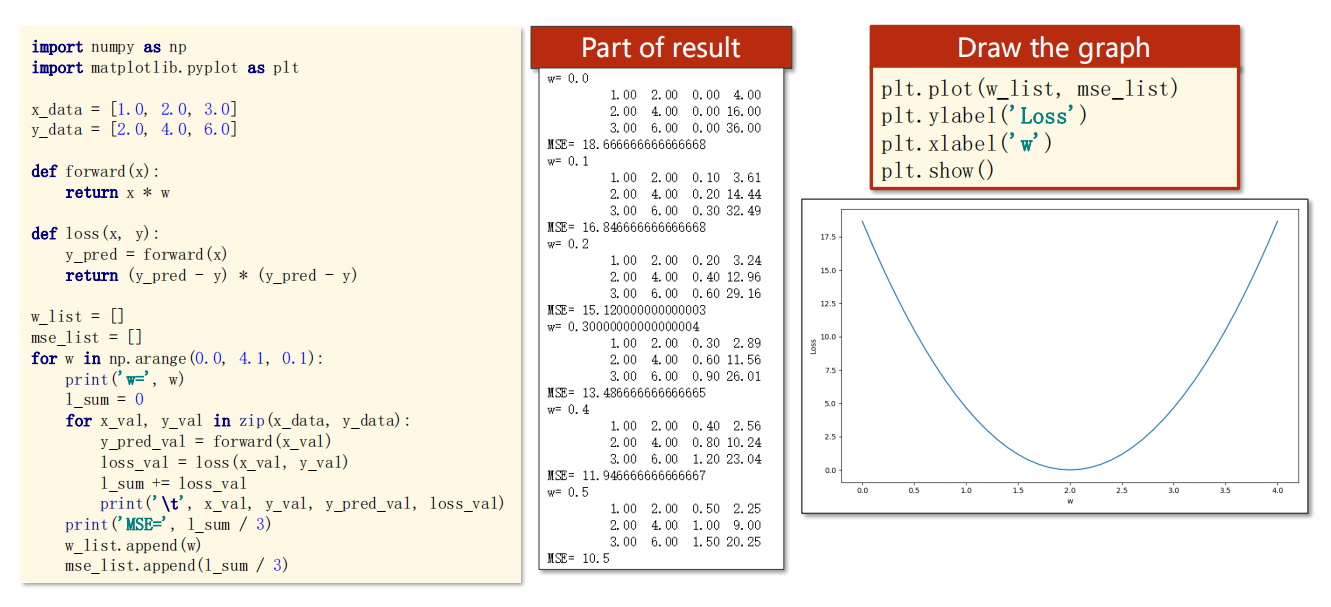
1 | import numpy as np |
1 | ------ |
1 | plt.plot(w_list, mse_list) |
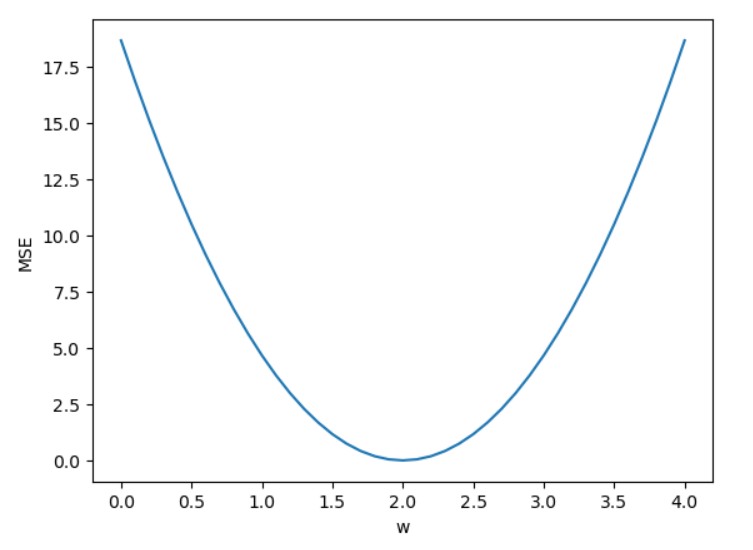
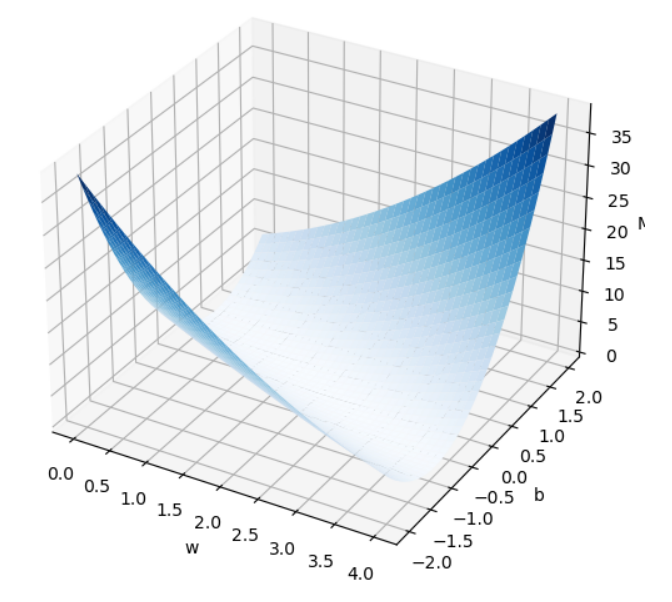
*2.4 课后题

绘图参考链接:
1 | import numpy as np |
1 | ------ |
1 | import matplotlib.pyplot as plt |
03、Gradient Descent
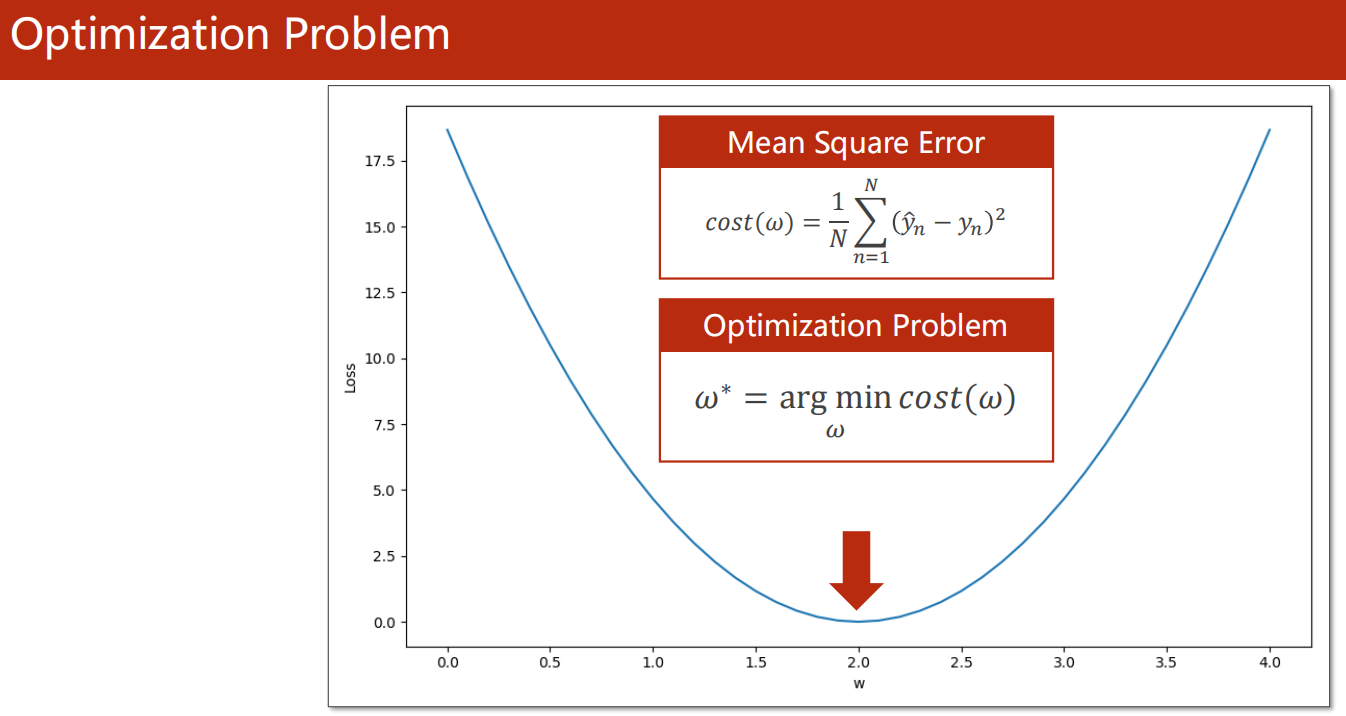
3.1 优化问题
- 就是寻找 使得损失函数最小的 参数 的值
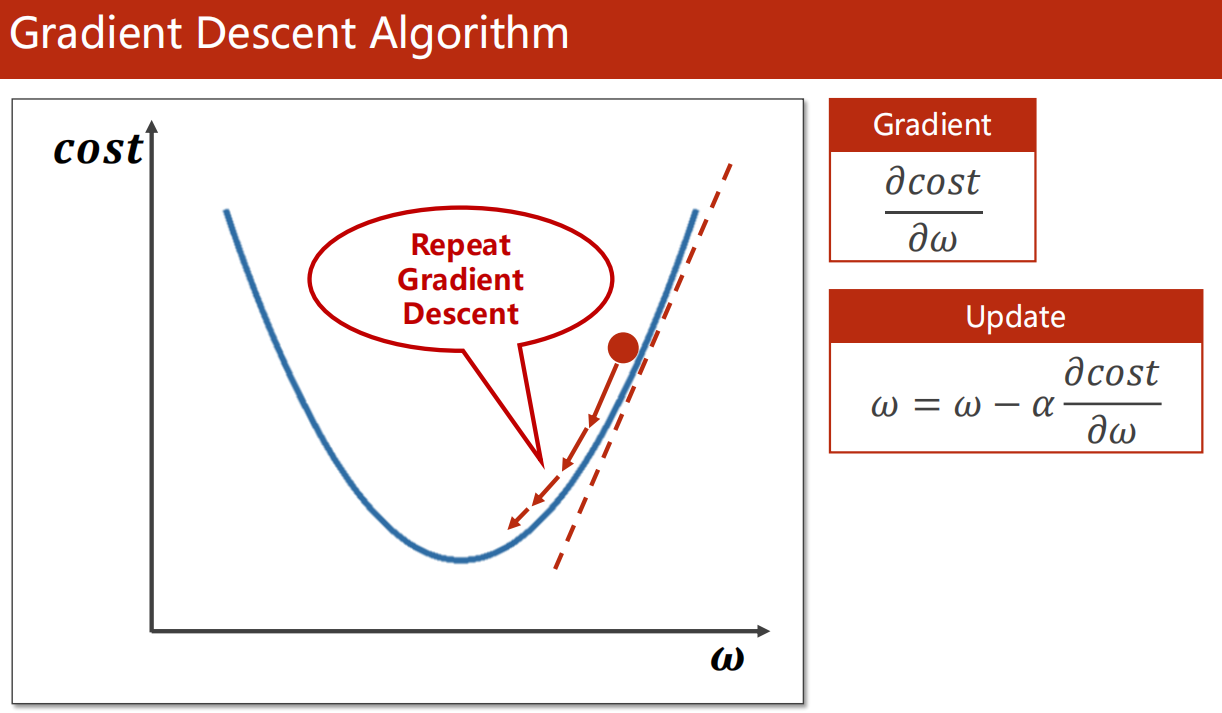
3.2 梯度下降算法

3.3 代码实现
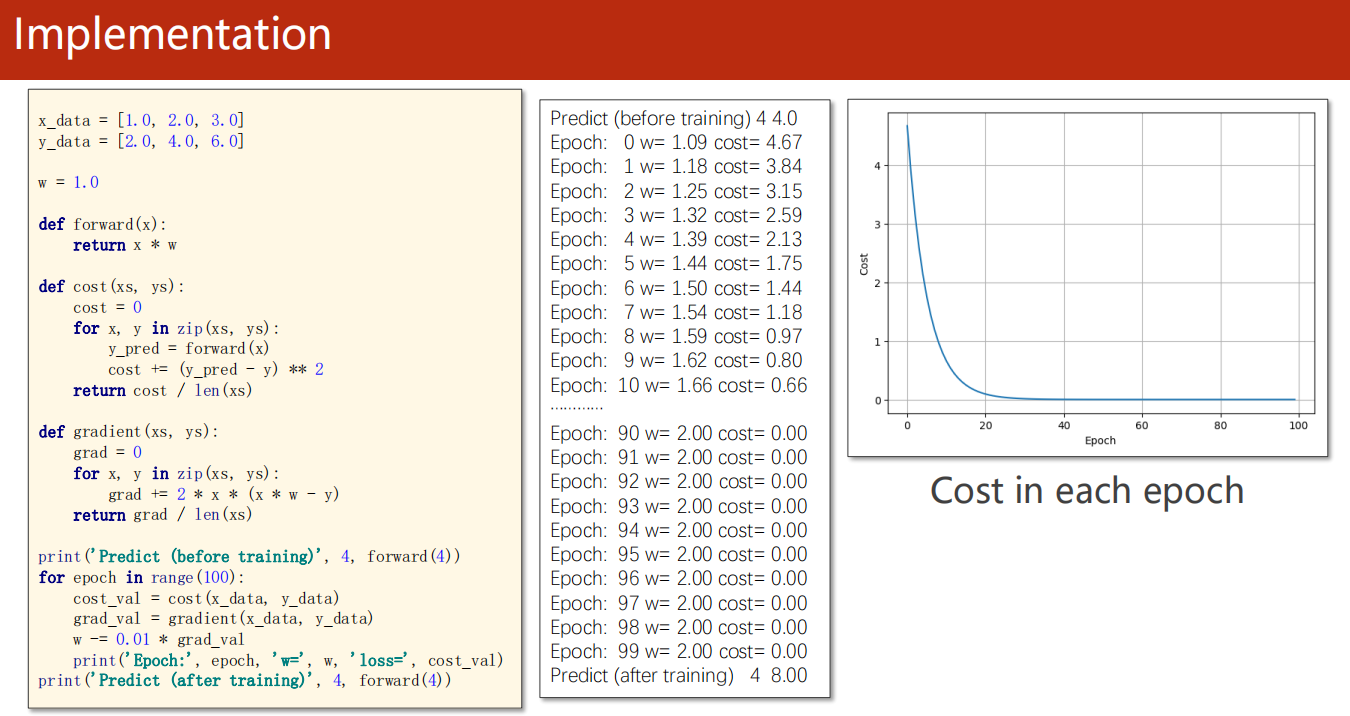
1 | import numpy as np |
1 | Predict (before training) 4 4.0 |
1 | import matplotlib.pyplot as plt |
对于学习率 的选取不能太大,不能太小
太大,会直接越过最优点,导致学习失败
太小,学习速率太慢,甚至无法达到最优点
比如这里,如果
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Epoch: 0 w= 1.0 loss= 4.666666666666667
Epoch: 1 w= 10.333333333333334 loss= 324.0740740740741
Epoch: 2 w= -67.44444444444446 loss= 22505.144032921817
Epoch: 3 w= 580.7037037037038 loss= 1562857.2245084594
Epoch: 4 w= -4820.530864197532 loss= 108531751.70197636
Epoch: 5 w= 40189.75720164609 loss= 7536927201.526134
Epoch: 6 w= -334895.9766803841 loss= 523397722328.2038
Epoch: 7 w= 2790818.472336534 loss= 36347064050569.695
Epoch: 8 w= -23256801.93613778 loss= 2524101670178451.0
Epoch: 9 w= 193806701.46781486 loss= 1.752848382068369e+17
...
Epoch: 97 w= 2.0865035760330826e+89 loss= 2.0316320139727924e+179
Epoch: 98 w= -1.7387529800275687e+90 loss= 1.4108555652588838e+181
Epoch: 99 w= 1.4489608166896407e+91 loss= 9.797608092075583e+182
Predict (after training) 4 -4.829869388965469e+92
- 如果$ \alpha = 0.1$
其实发现,这里反而是0.1时结果最好。
但是你看 的变化,实际上不好,只是恰好滚入了 。
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Epoch: 0 w= 1.0 loss= 4.666666666666667
Epoch: 1 w= 1.9333333333333336 loss= 0.020740740740740594
Epoch: 2 w= 1.9955555555555555 loss= 9.218106995885089e-05
Epoch: 3 w= 1.9997037037037038 loss= 4.096936442612555e-07
Epoch: 4 w= 1.9999802469135801 loss= 1.820860641186282e-09
Epoch: 5 w= 1.999998683127572 loss= 8.092713960827921e-12
Epoch: 6 w= 1.9999999122085048 loss= 3.5967617630537535e-14
Epoch: 7 w= 1.9999999941472337 loss= 1.598560741415451e-16
Epoch: 8 w= 1.9999999996098157 loss= 7.104714637326717e-19
Epoch: 9 w= 1.9999999999739877 loss= 3.1576645553726146e-21
Epoch: 10 w= 1.9999999999982658 loss= 1.4035793259433332e-23
Epoch: 11 w= 1.9999999999998845 loss= 6.221483005843047e-26
Epoch: 12 w= 1.9999999999999922 loss= 2.7841859573644085e-28
Epoch: 13 w= 1.9999999999999993 loss= 1.791371638939381e-30
Epoch: 14 w= 2.0 loss= 0.0
Epoch: 15 w= 2.0 loss= 0.0
Epoch: 16 w= 2.0 loss= 0.0
Epoch: 17 w= 2.0 loss= 0.0
...
Epoch: 99 w= 2.0 loss= 0.0
Predict (after training) 4 8.0
3.4 随机梯度下降
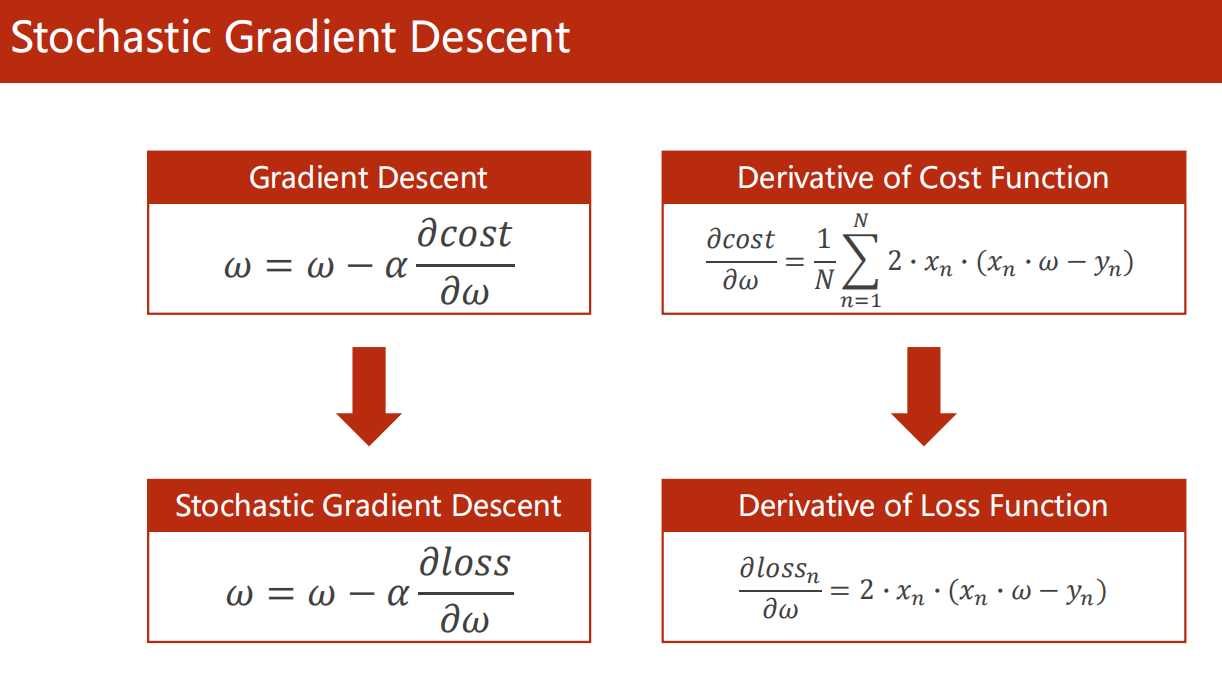

1 | import numpy as np |
1 | Predict (before training) 4 4.0 |
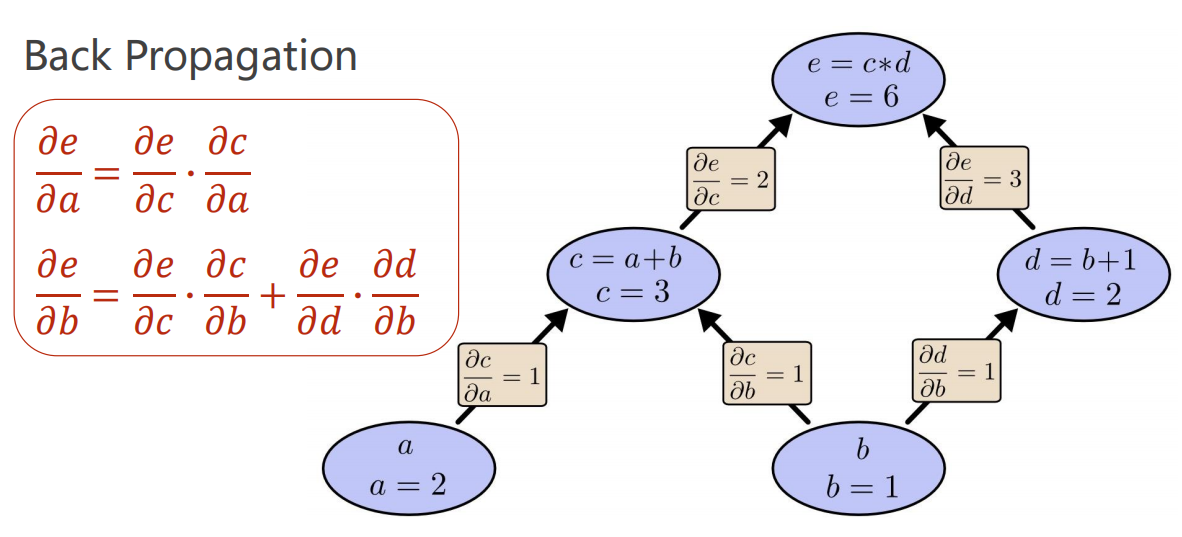
04、Back Propagation
4.1 引入
-
在前面例子中,我们是如何计算 损失函数 对 参数 的偏导数?
我们是直接手工计算,化简得到的。
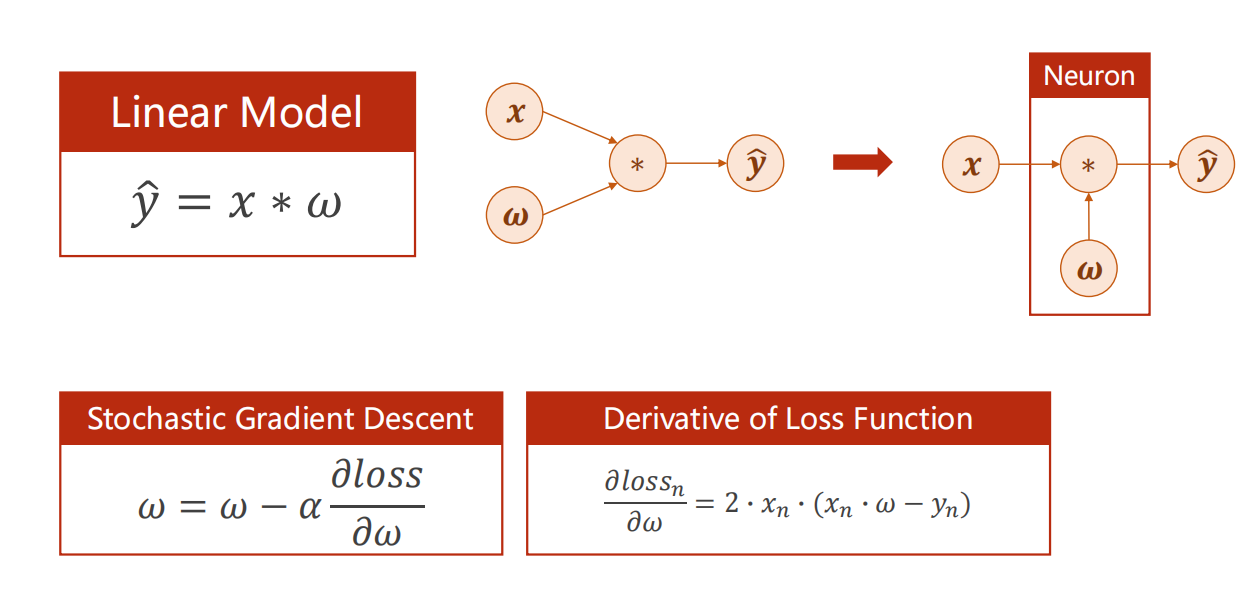
-
当模型很简单时,这么做当然是可行的。
但是若模型如下图,每一层会出现很多的 参数 ,且交错复杂,此时就不可行了。
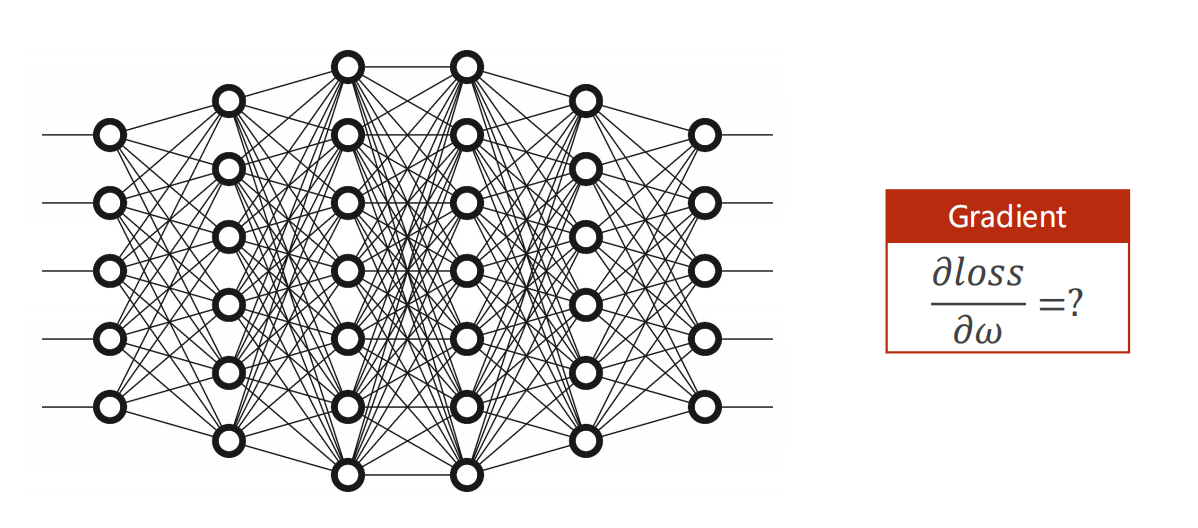
4.2 计算图
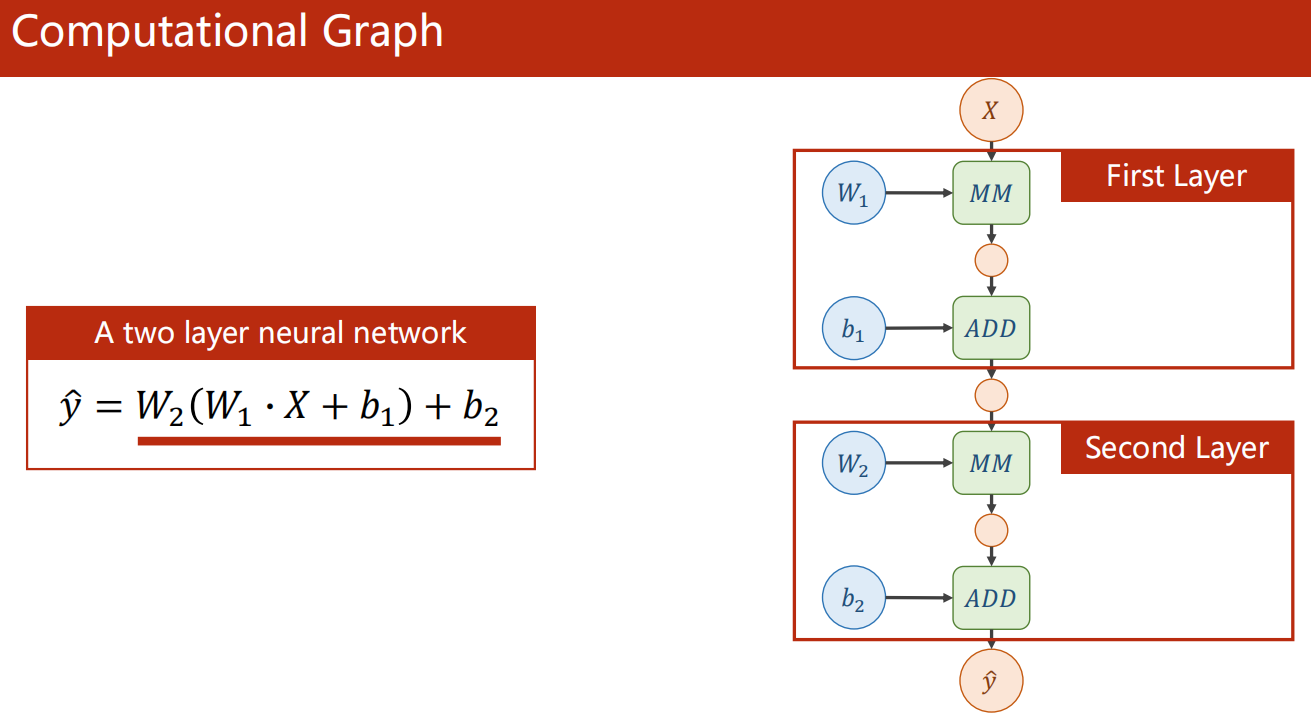
-
思考:连续两层 Linear ?
直接的连续两层 Linear 可以说是没有意义的。
因为实际上,可以直接化简发现,实际上一层就能达到这里所谓“两层”的效果。
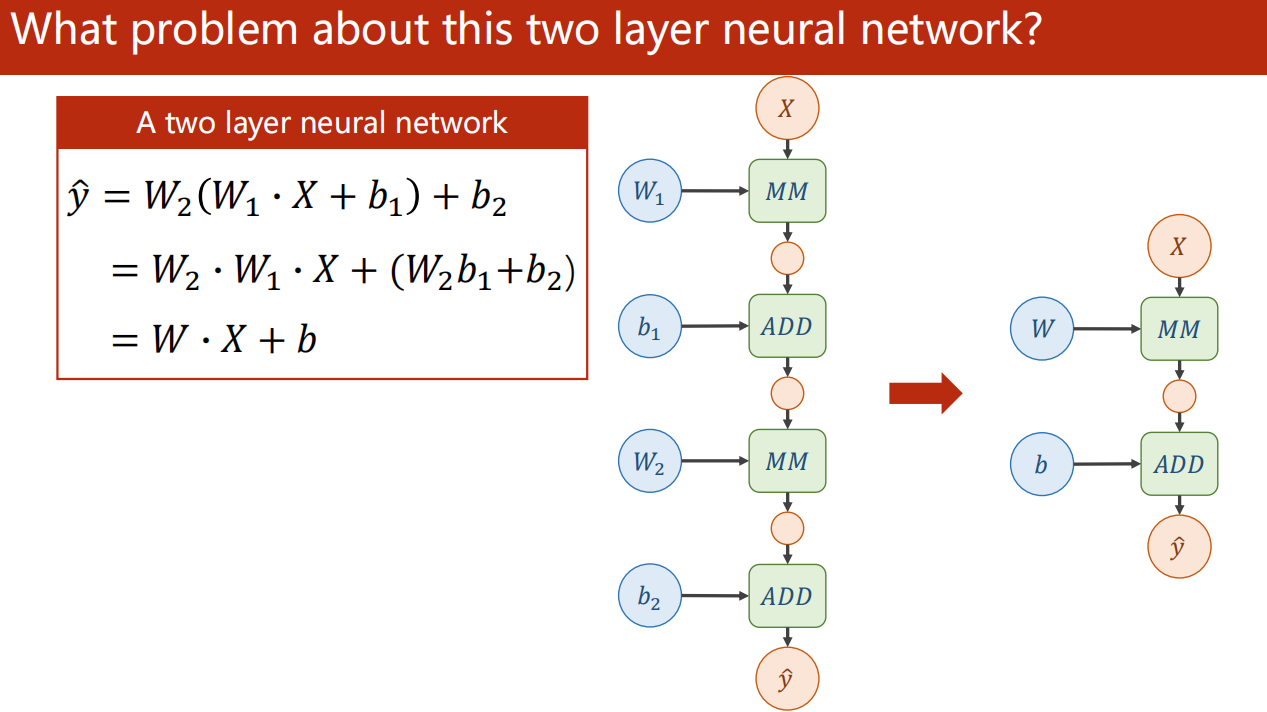
那是什么导致实际上一层就能达到两层的效果?
因为 Linear 本身的特性——线性!
因此,为了消除这个问题,我们需要进行 非线性激活。
在进入下一层 Linear 之前,先进行 非线性变换,再作为下一层 Linear 的输入。
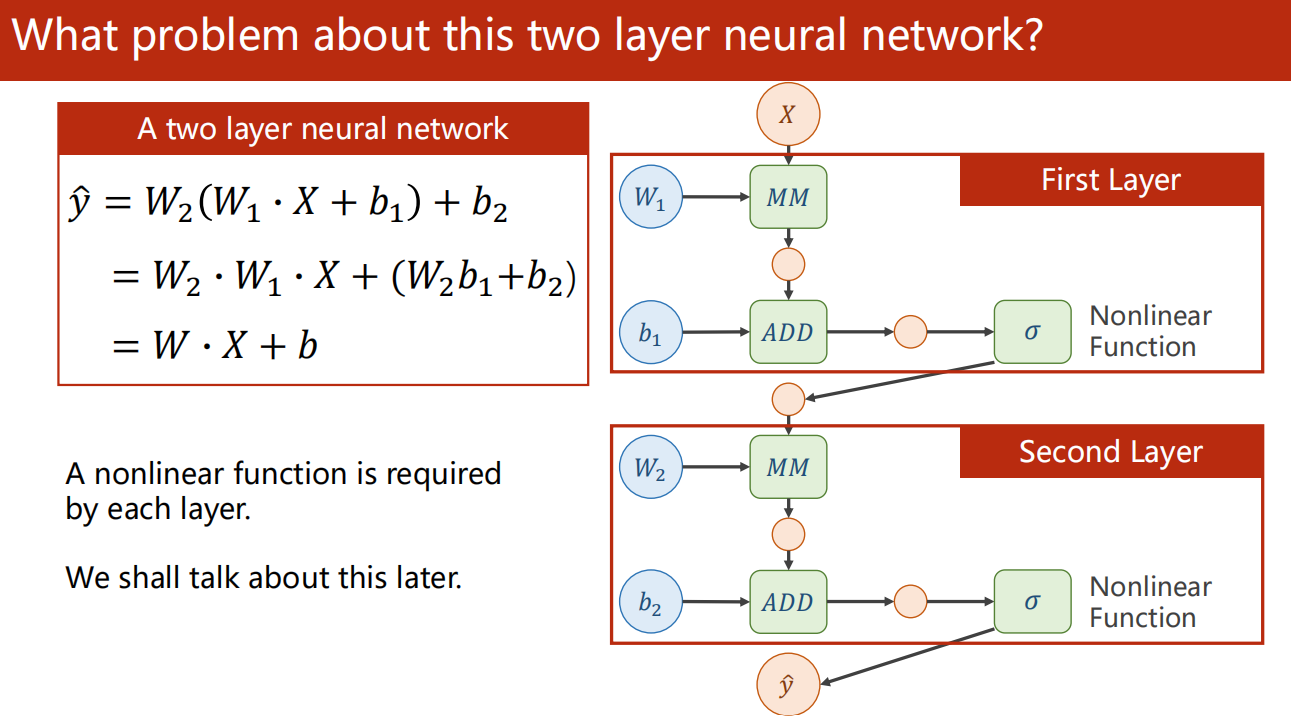
由于两层 Linear 之间有非线性函数存在,自然使得没办法把两次的线性变换化简为一次线性变换了。
由此,间接的连续两层 Linear 就有意义了。
4.3 Chain Rule 链式法则
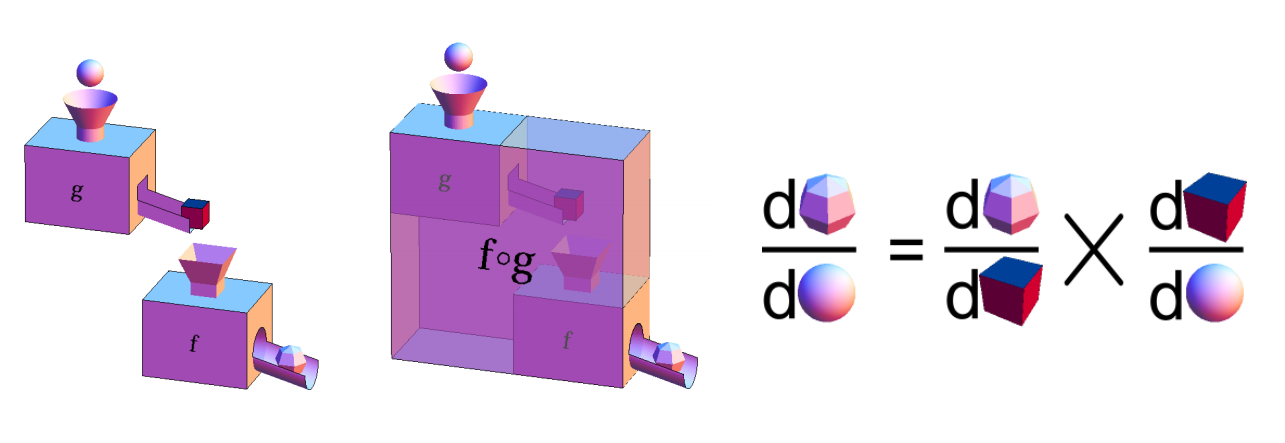
- 链式法则的使用
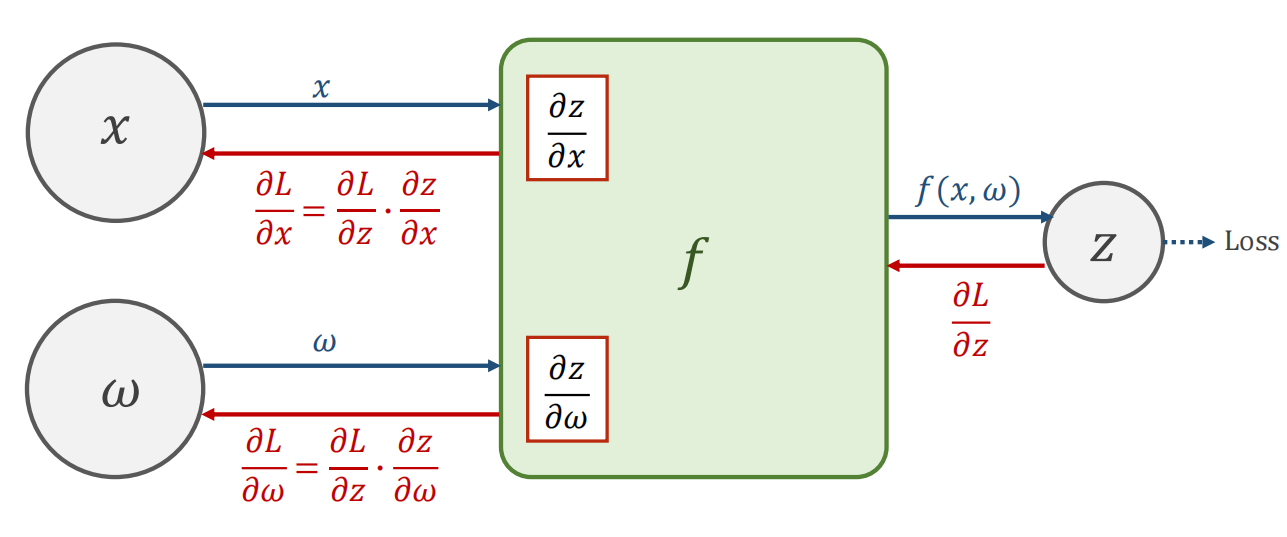
- 举例:
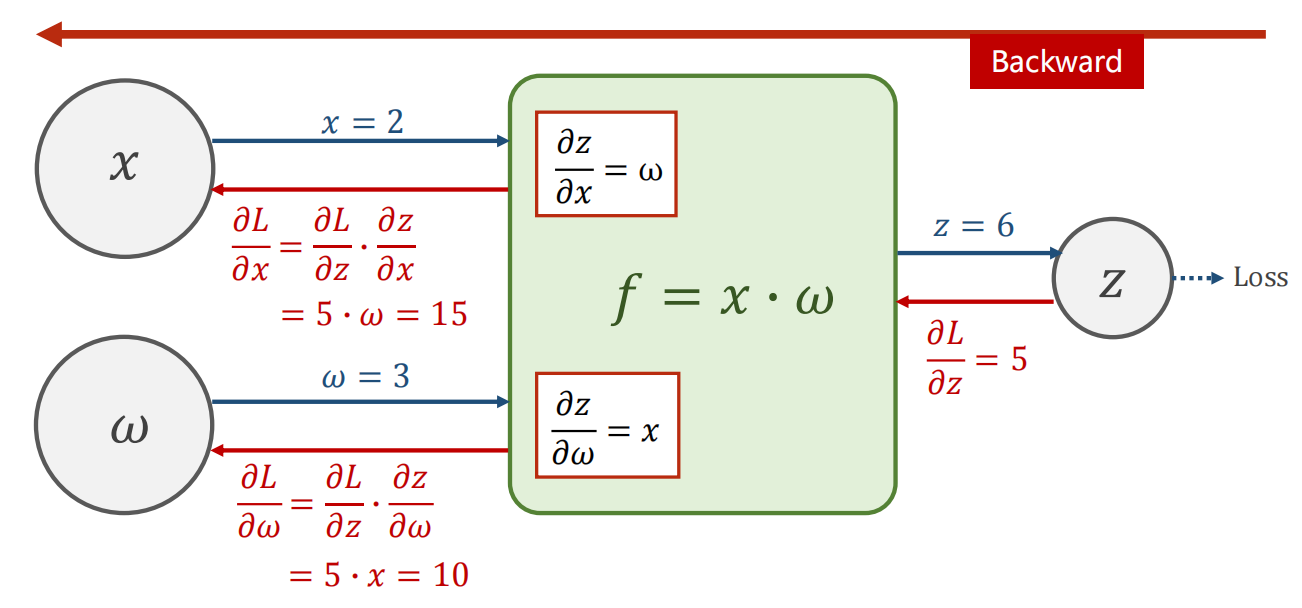
4.4 Linear Model 计算图
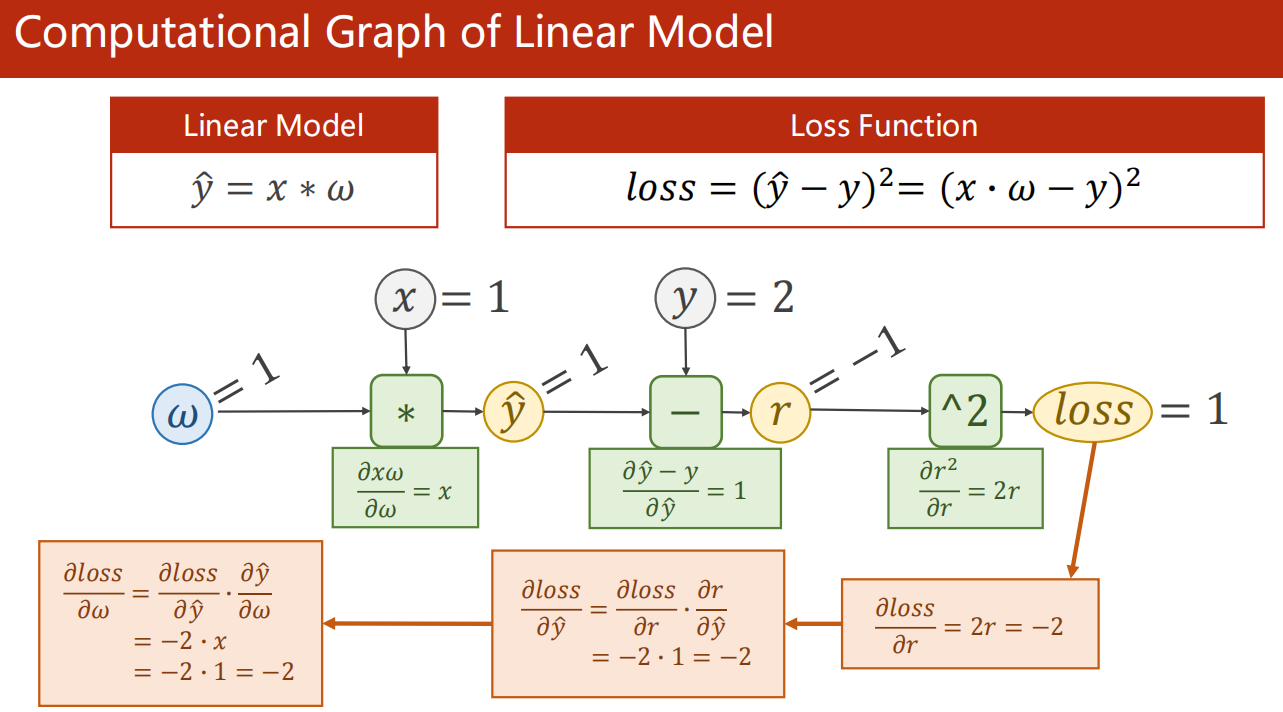
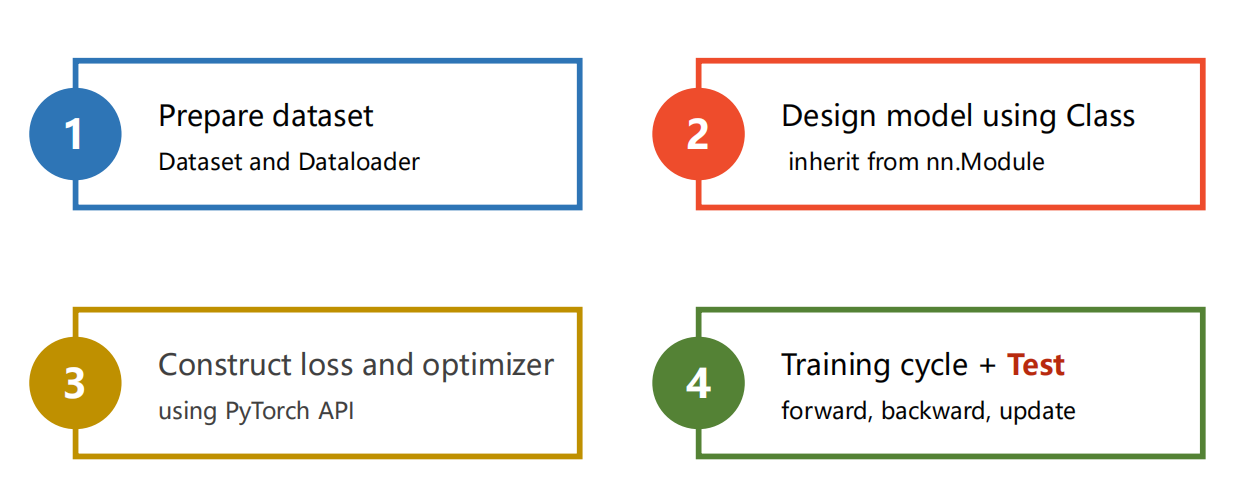
05、Linear Regression with Pytorch
函数解释可参考官网Pytorch Tutorial
5.1 流程速览
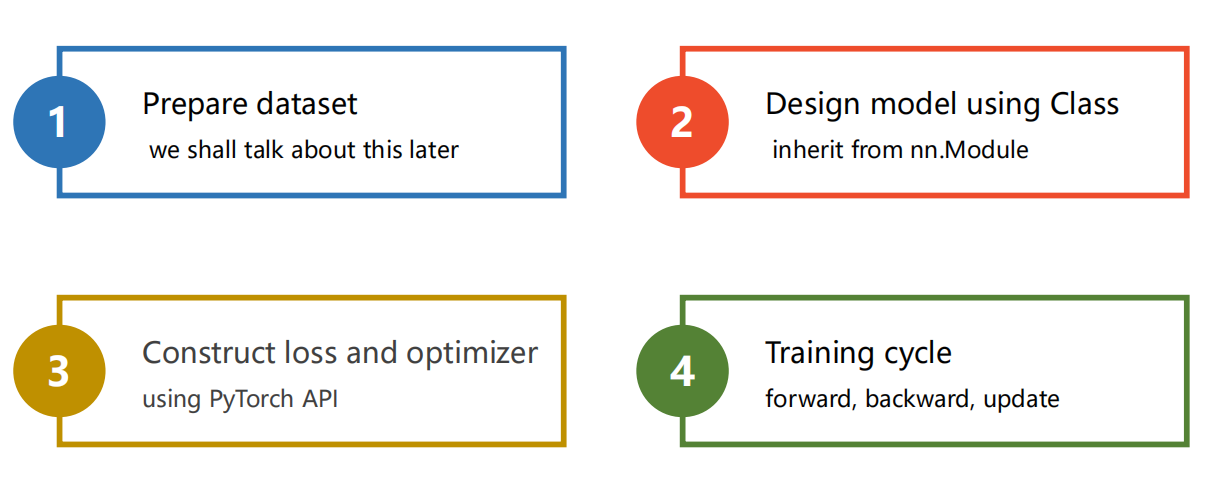
-
1、准备数据集

-
2、设计模型
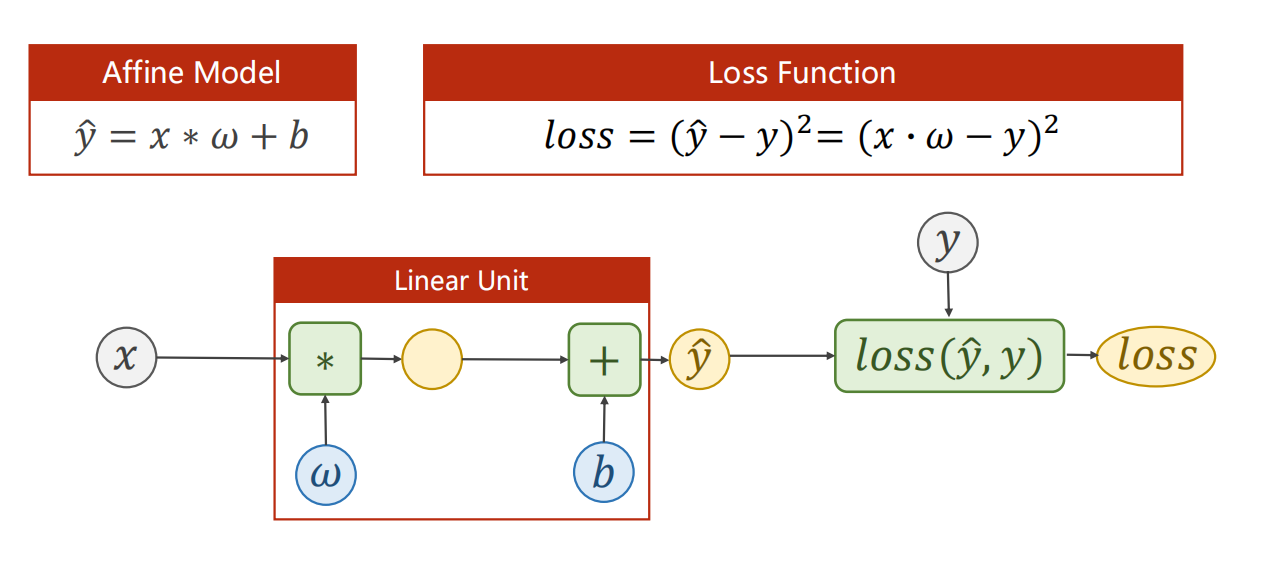
-
3、构建损失函数和优化器

-
4、训练轮次
- forward
- backward
- update

5.2 代码实现
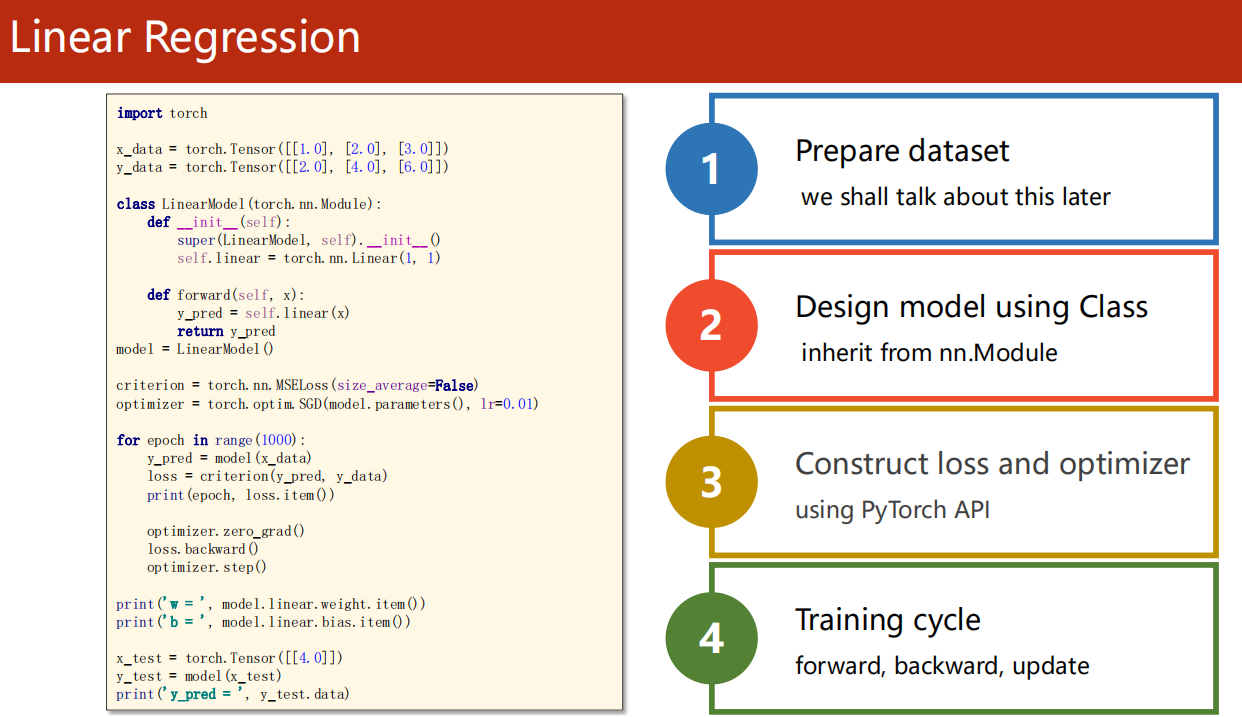
1 | import torch |
1 | 0 31.277143478393555 |
06、Logistic Regression
6.1 分类问题

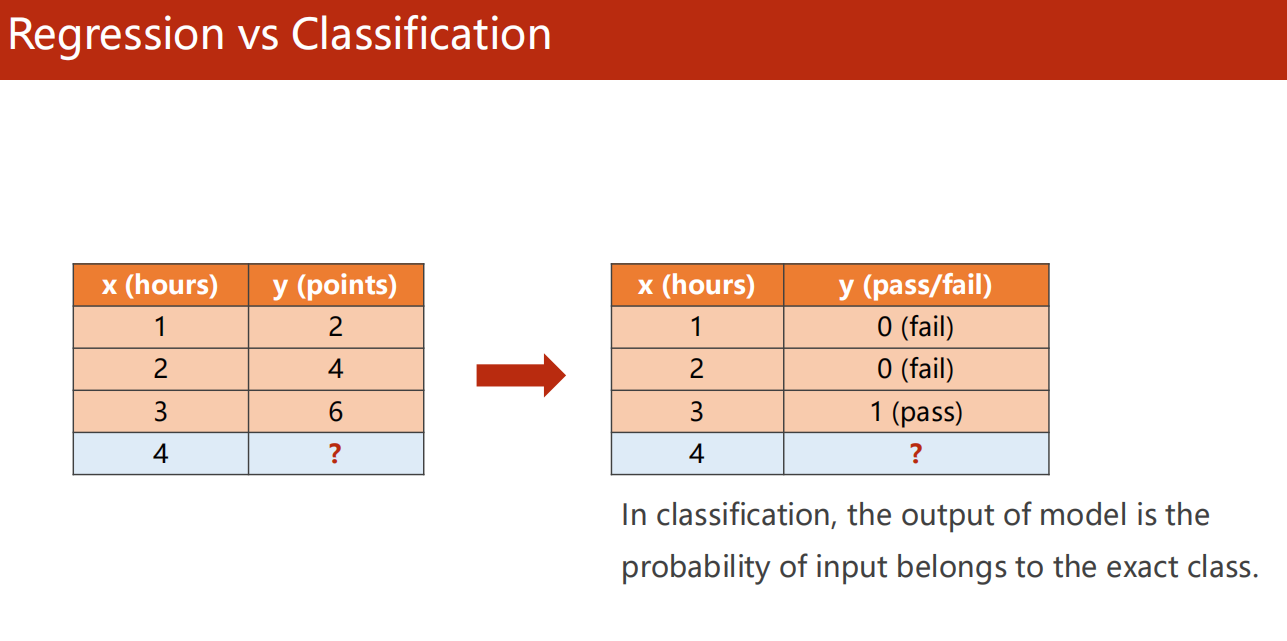
6.2 概率函数
- 需要把数据值从 映射到
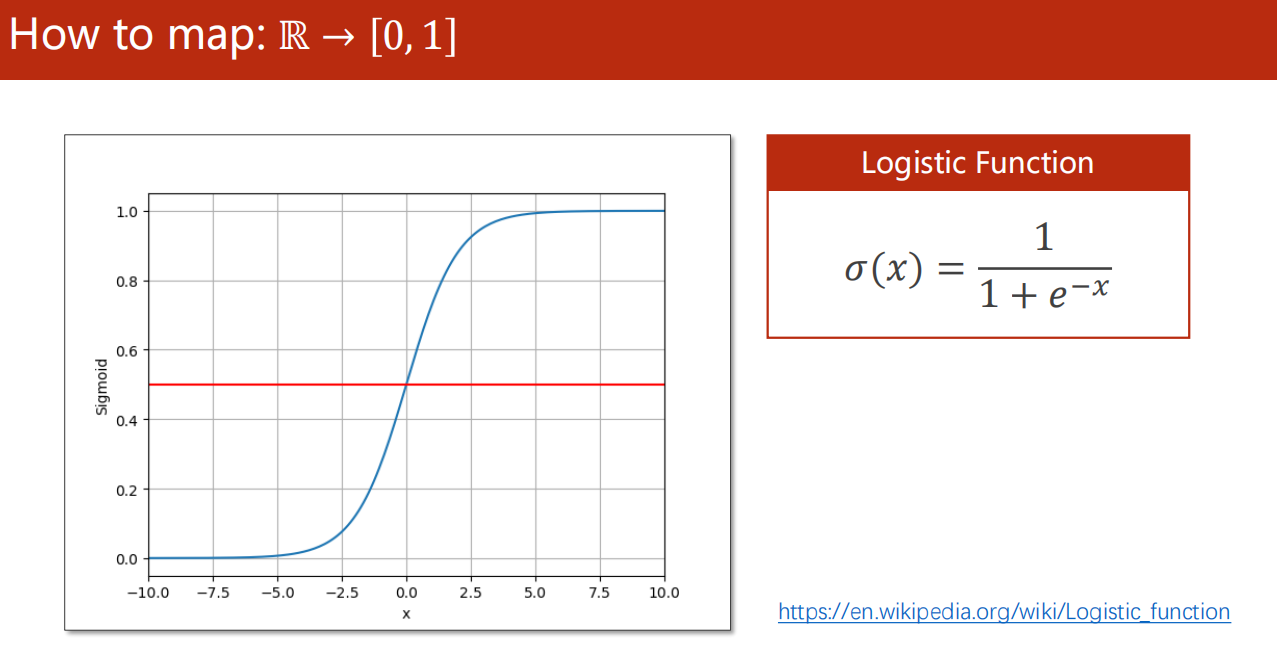
6.3 逻辑斯蒂回归模型
-
实际上,就在 层加一个 函数把值映射到 即可
-
模型
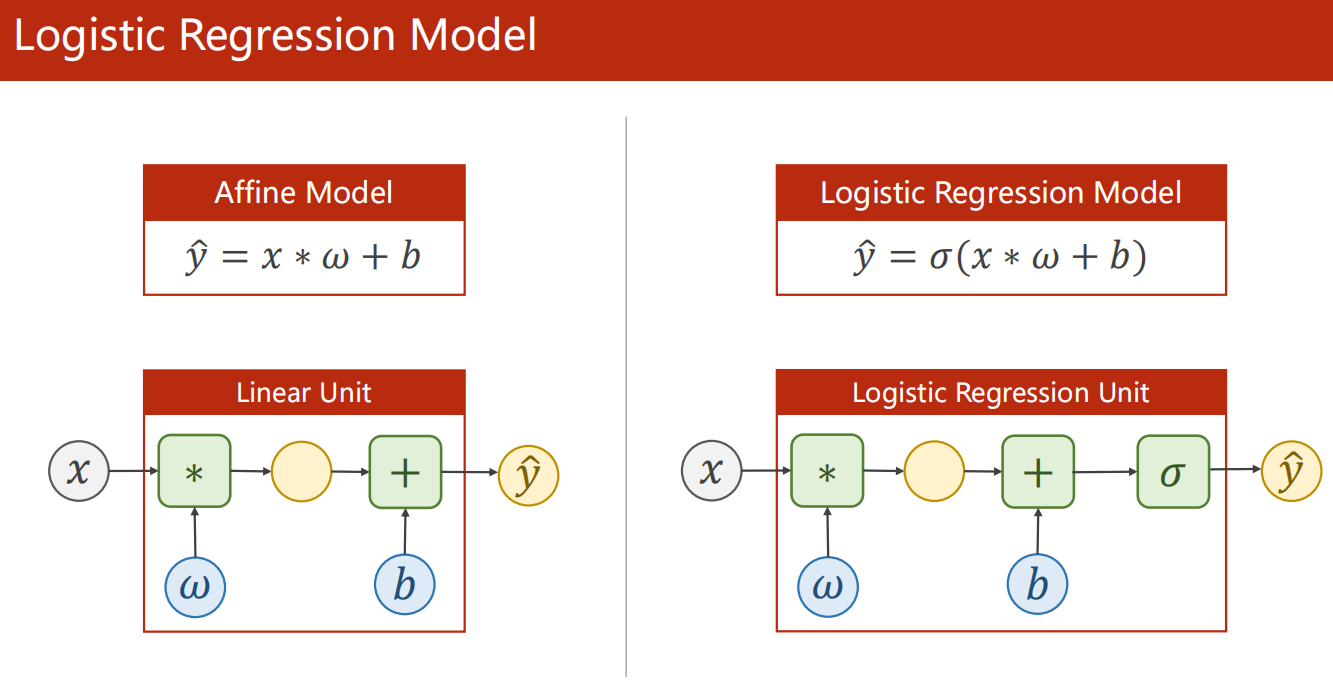

-
损失函数

- 例如:
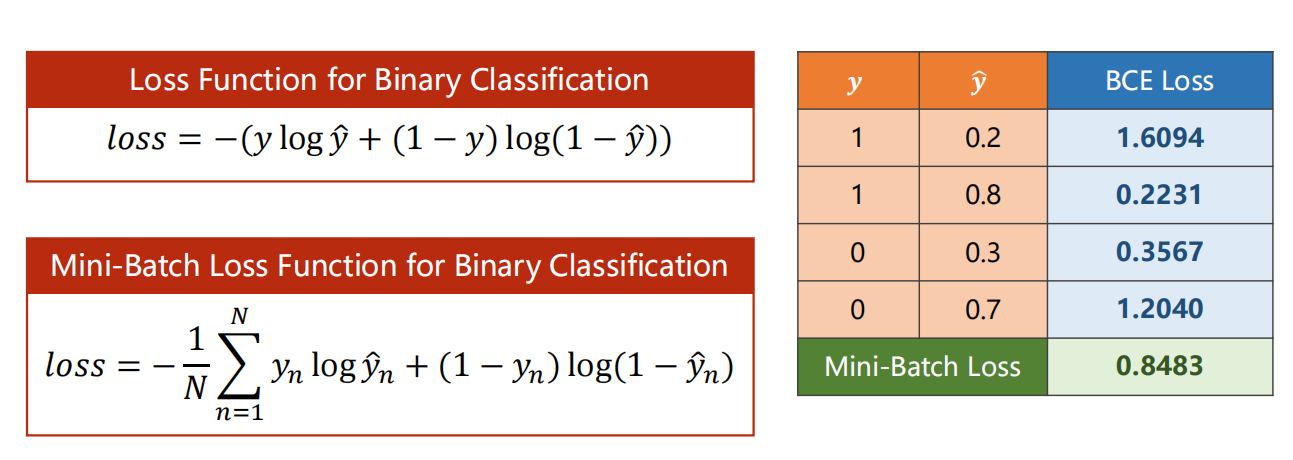
- 其中 总的 loss 函数调用为 BCELoss

6.4 代码实现
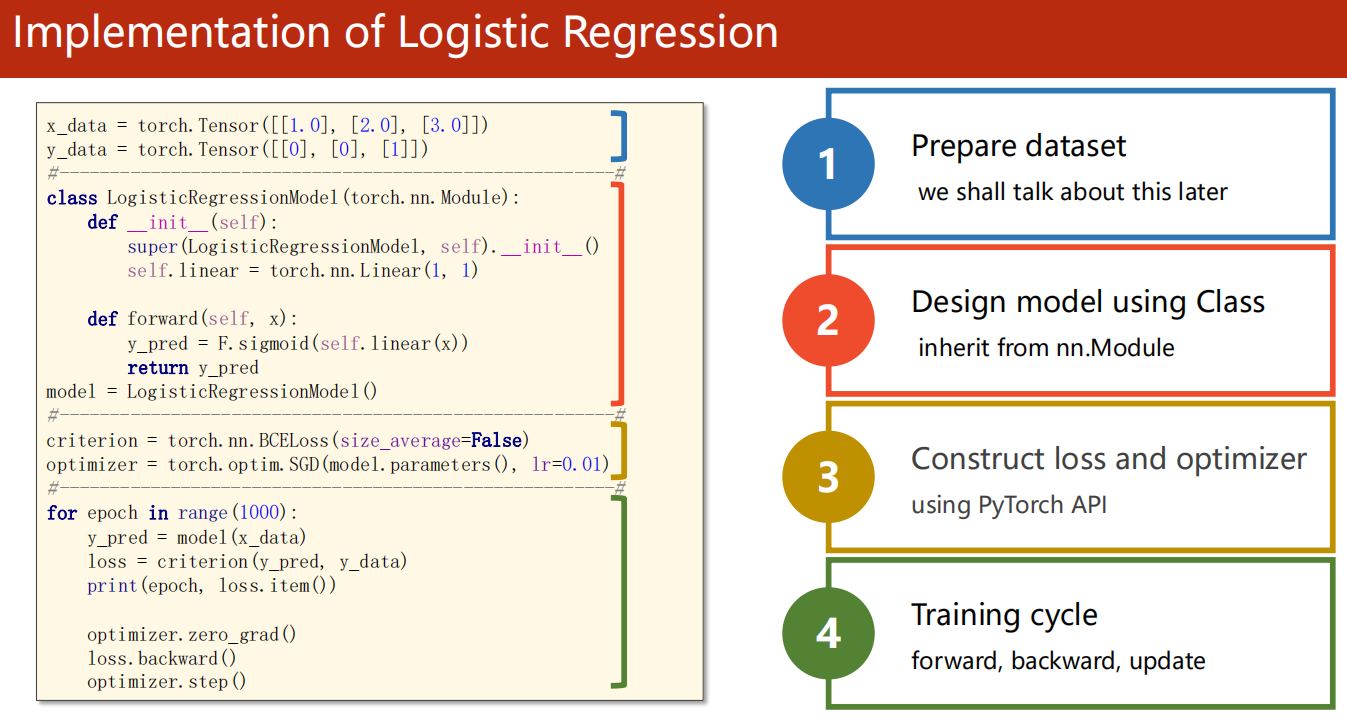
1 | import torch |
1 | 0 2.551990509033203 |
1 | import numpy as np |
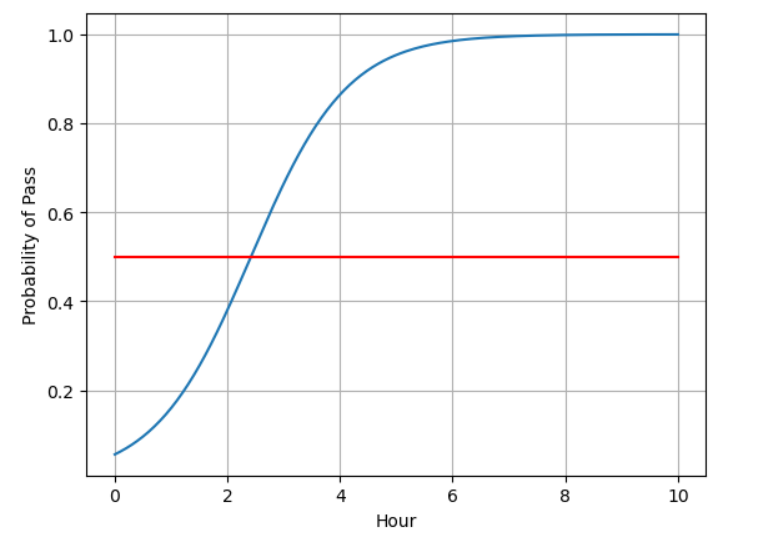
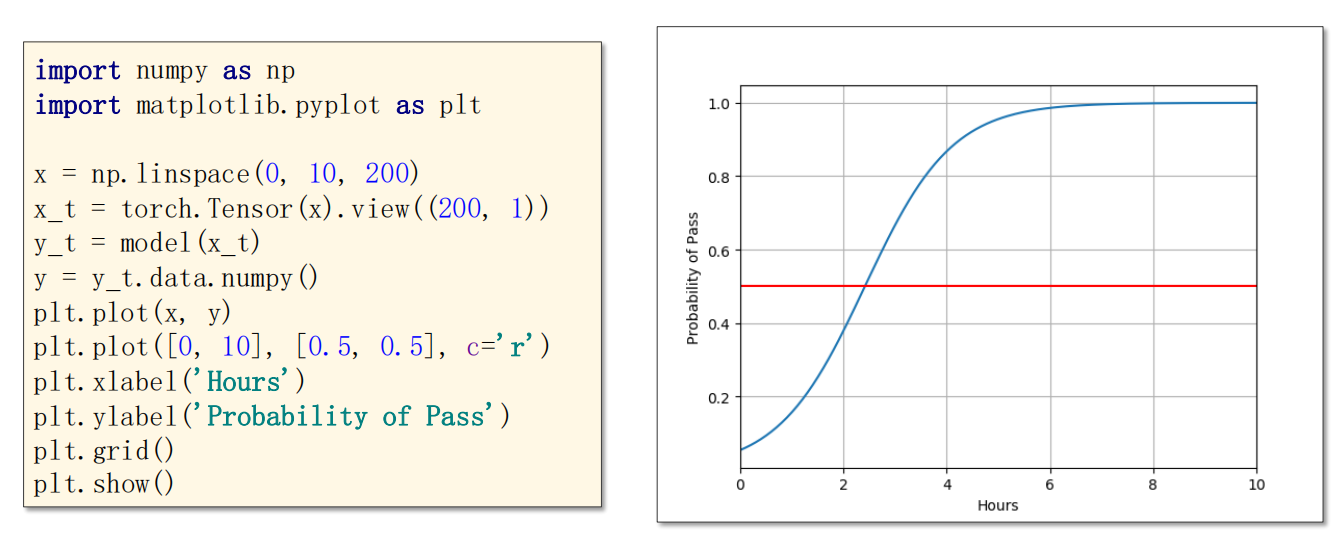
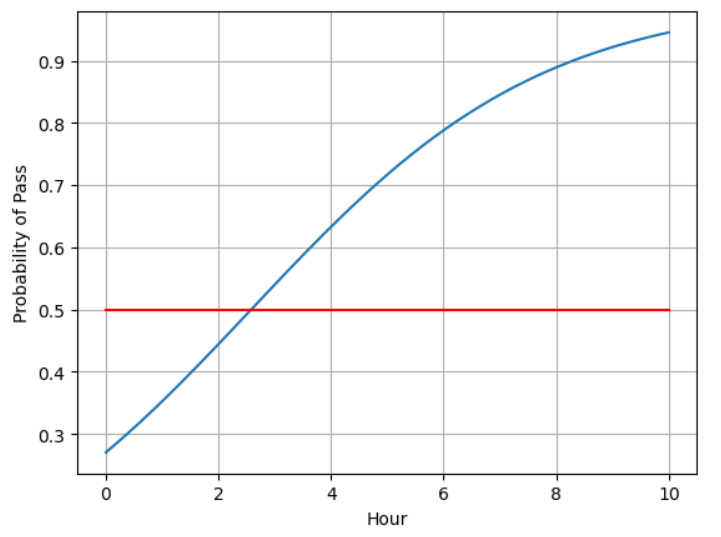
注意:训练一定要足够。
我第一次写错了代码,把epoch轮次写为了100,得到的比较粗糙,是下面这样的:
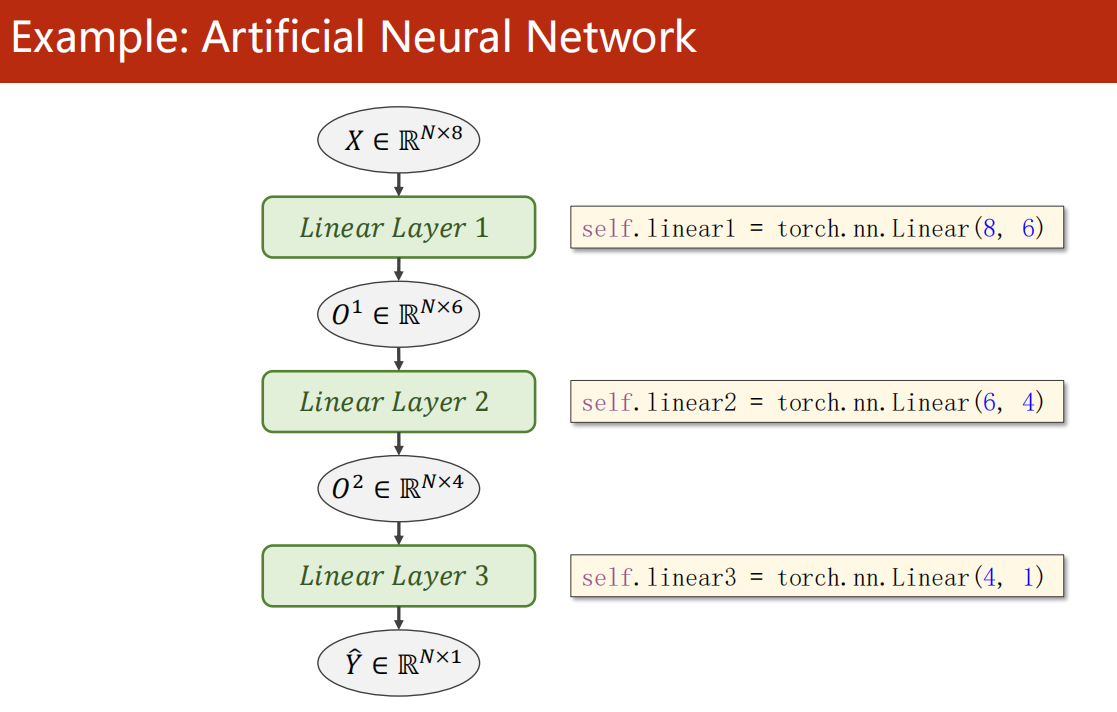
07、Multiple Dimension Input
7.1 多维特征数据集
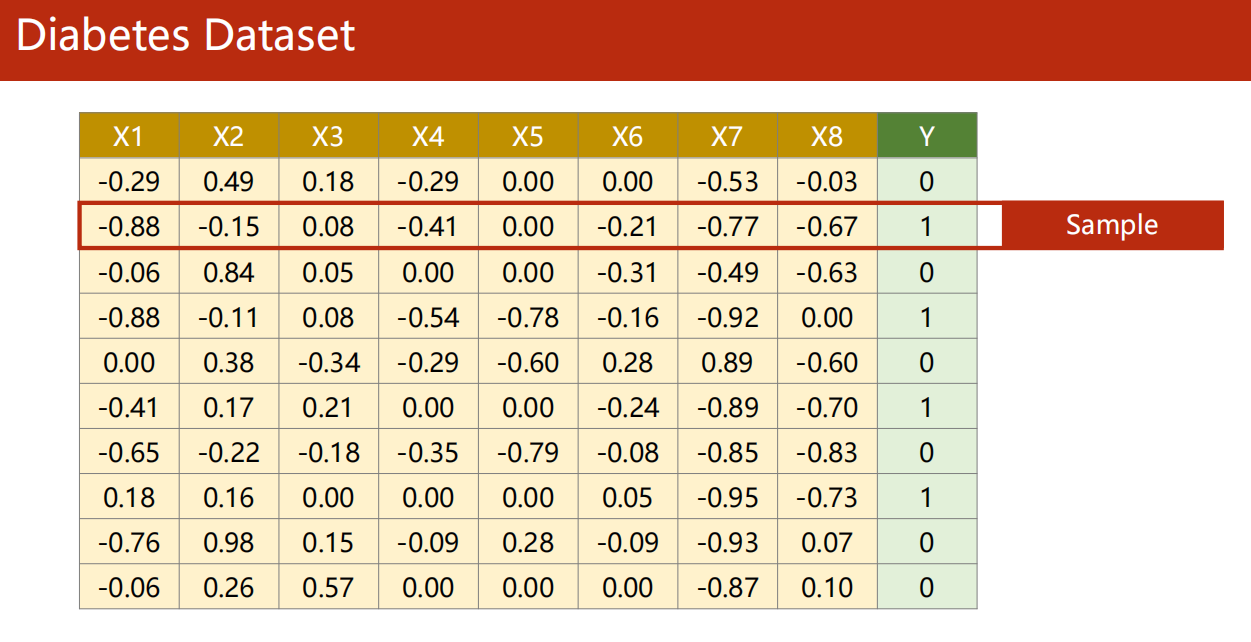
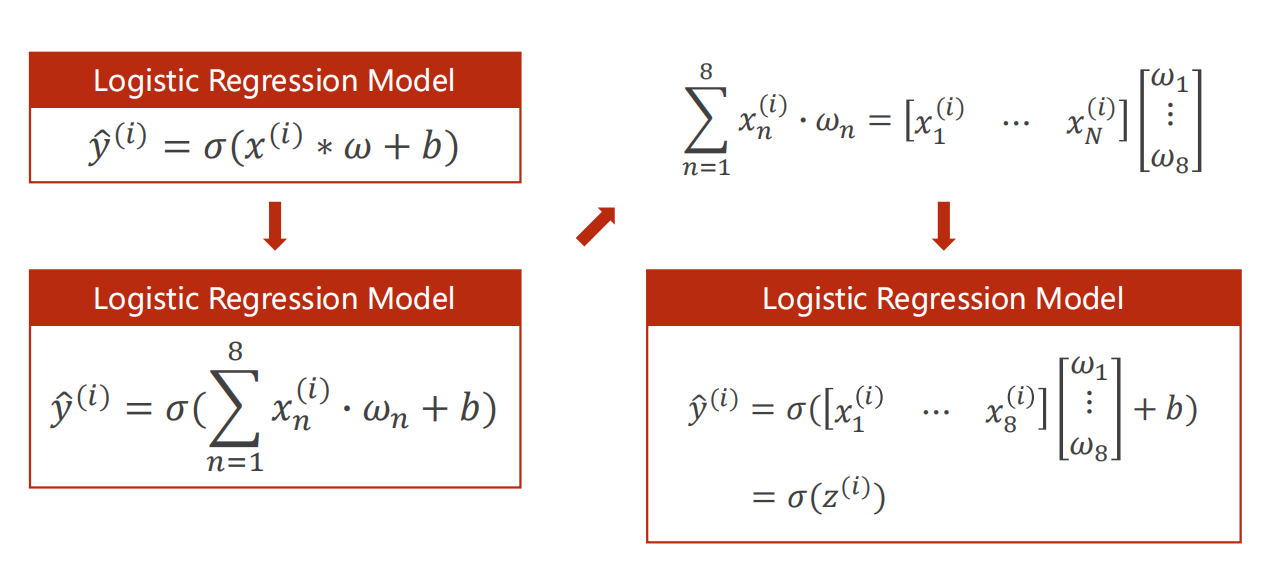
-
每一次 mini-batch
是 N 个样本,每个样本有 8 个特征。
线性变换到 1 个输出。

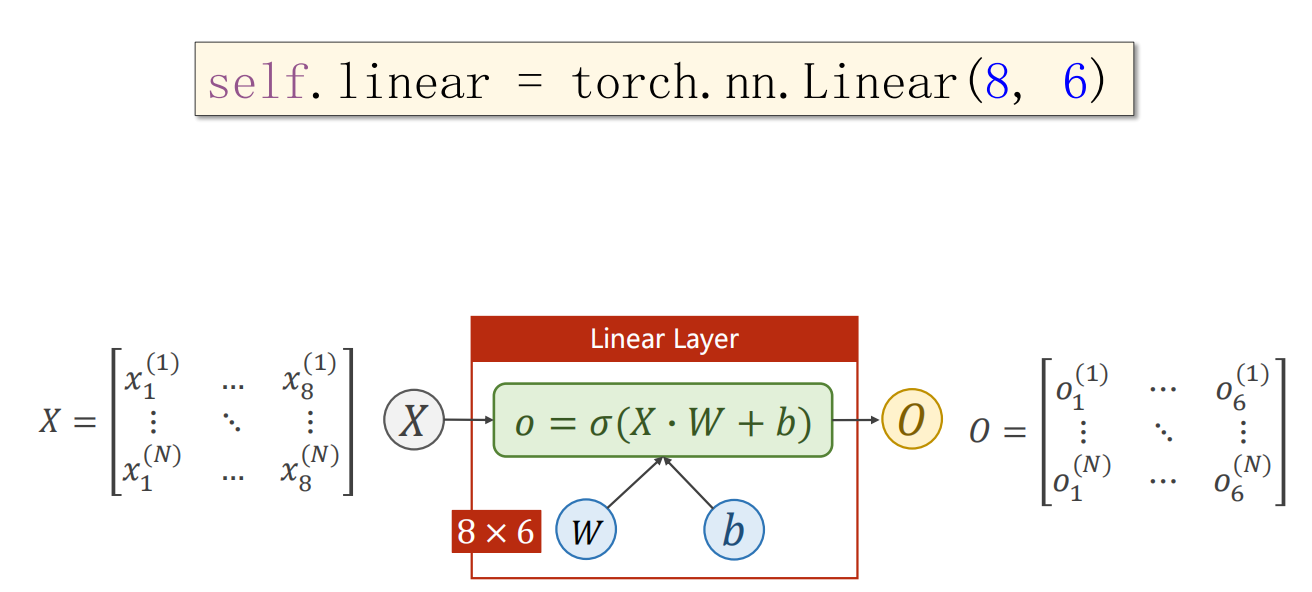
7.2 Linear 参数
- 第一个参数是输入 的维度
- 第二个参数是输出 的维度
这里的维度,指的是特征量的维度(几个特征量)。
而与 一次 mini-batch 的样本数量无关。
- 神经网络还是一样做法:
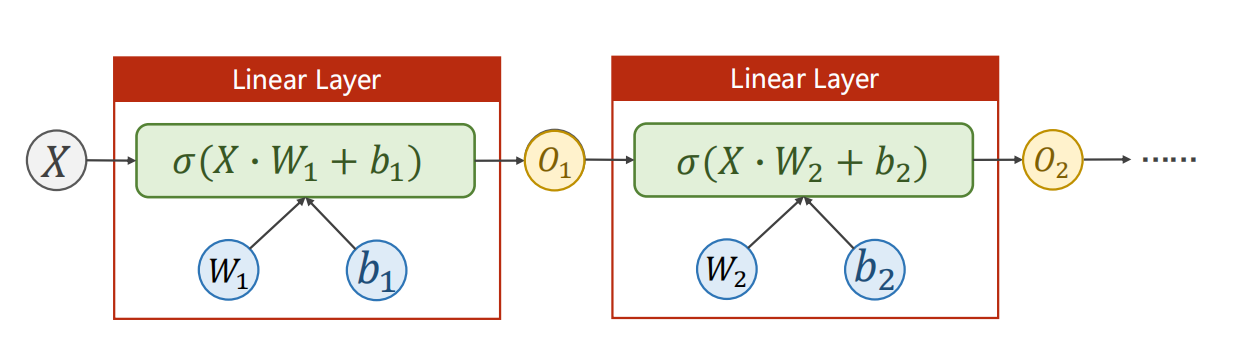
-
例如
注意每次线性层的输入输出的特征维度。
非线性层是不会改变维度的。
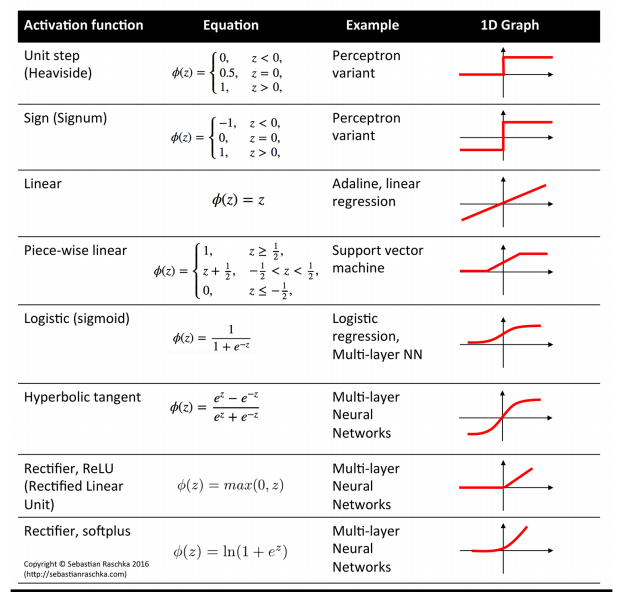
-
激活函数有很多
7.3 示例:糖尿病预测
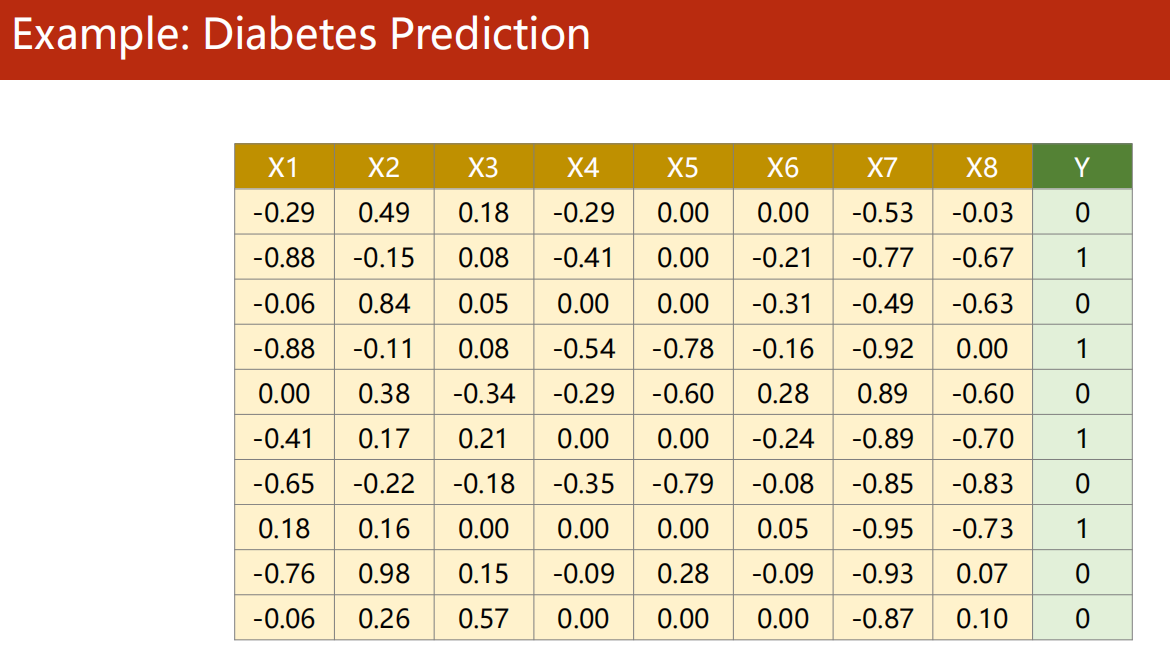
-
1、准备数据
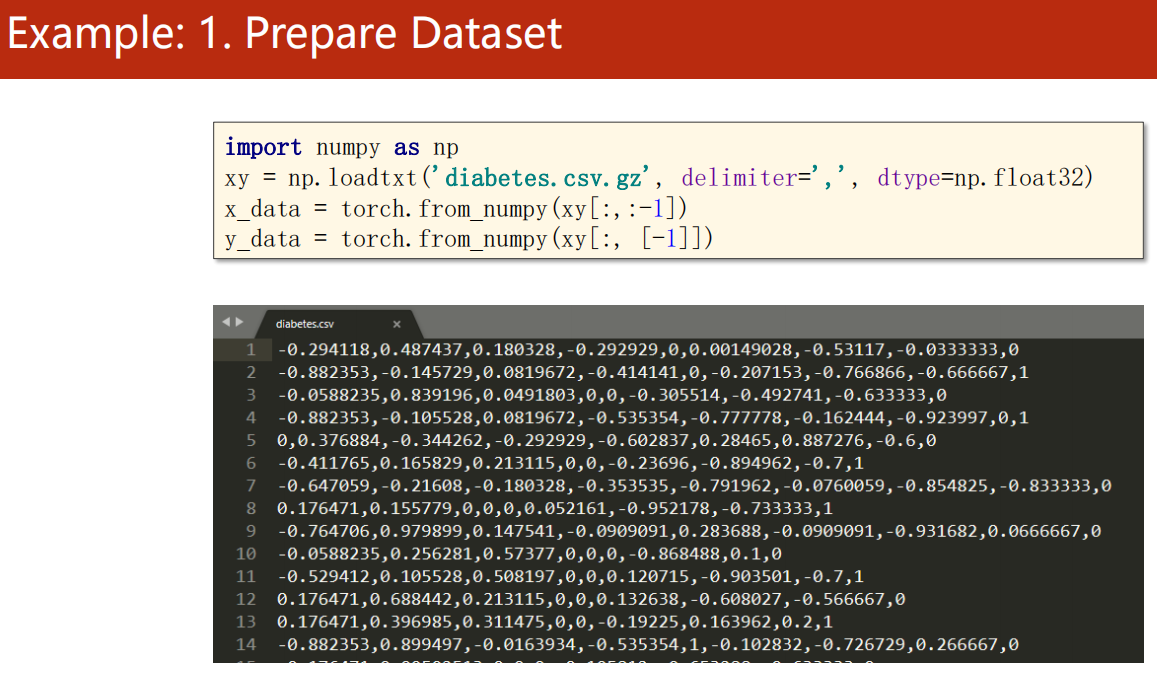
-
2、设计模型

-
3、构建损失函数、优化器

-
4、训练轮次
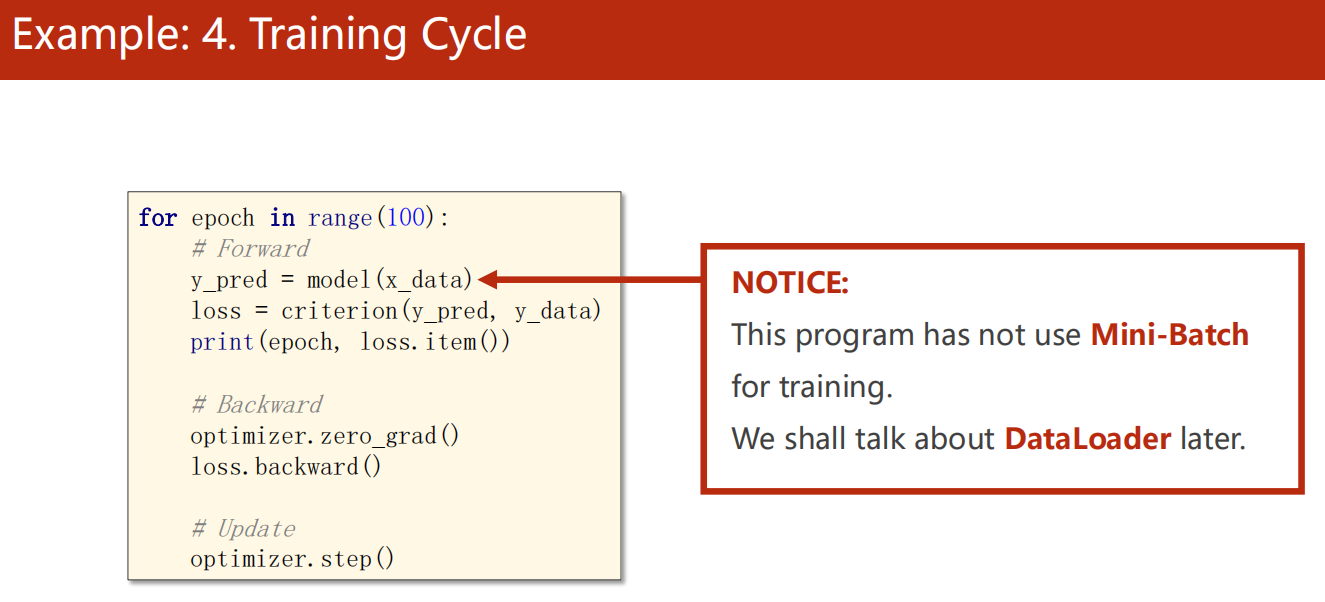
7.4 代码实现
1 | import numpy as np |
1 | 0 519.3440551757812 |
08、Dataset DataLoader
Windows 下若使用多线程,需要注意必须加
__main__
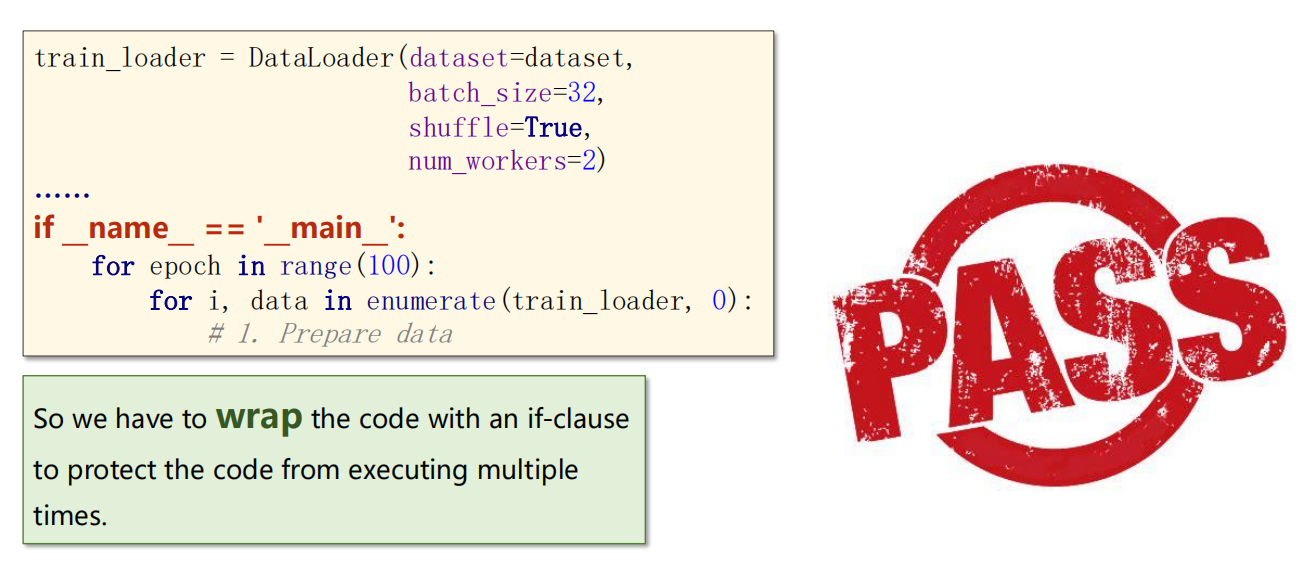
8.1 引入Epoch,BatchSize,Iterations
- 原本:我们是直接使用全部数据的
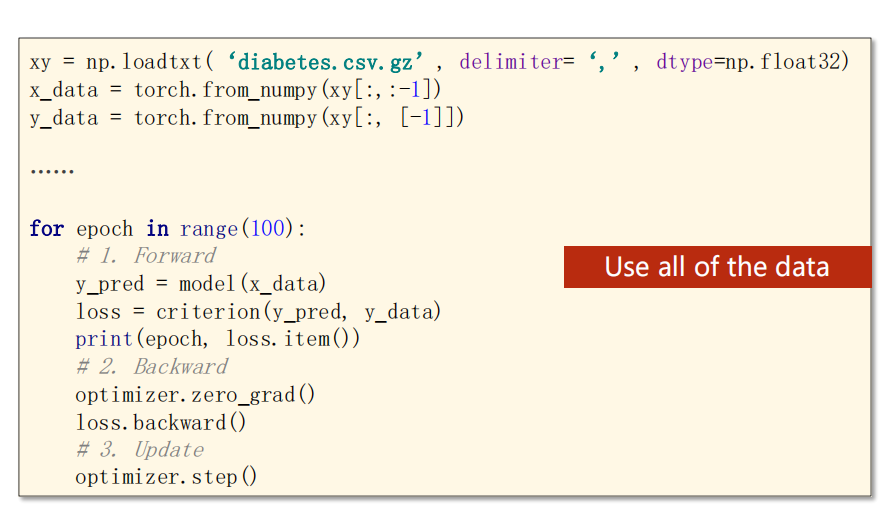
-
新概念

- 示例
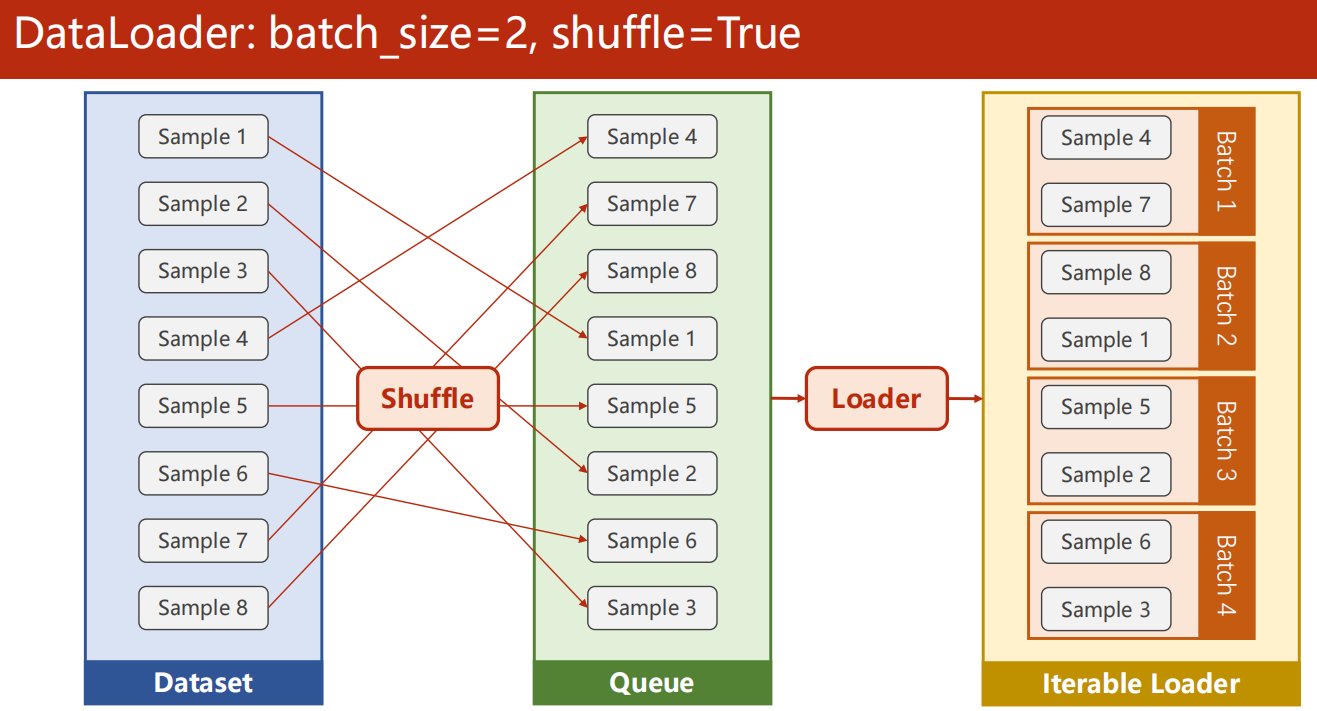
8.2 实现流程

- 必须实现以上三个函数,才能实例化 Dataset(Dataset是抽象类,本身无法被实例化为对象)
- DataLoader参数
- dataset 是 Dataset 对象
- batch_size 是 批次大小
- shuffle 是每次批次抽取前是否打乱分批(一般train时True,test时False)
- num_works 是多线程数目

-
完整流程

8.3 代码实现
1 | import numpy as np |
这里运行出错,不知
*8.4 可用数据集
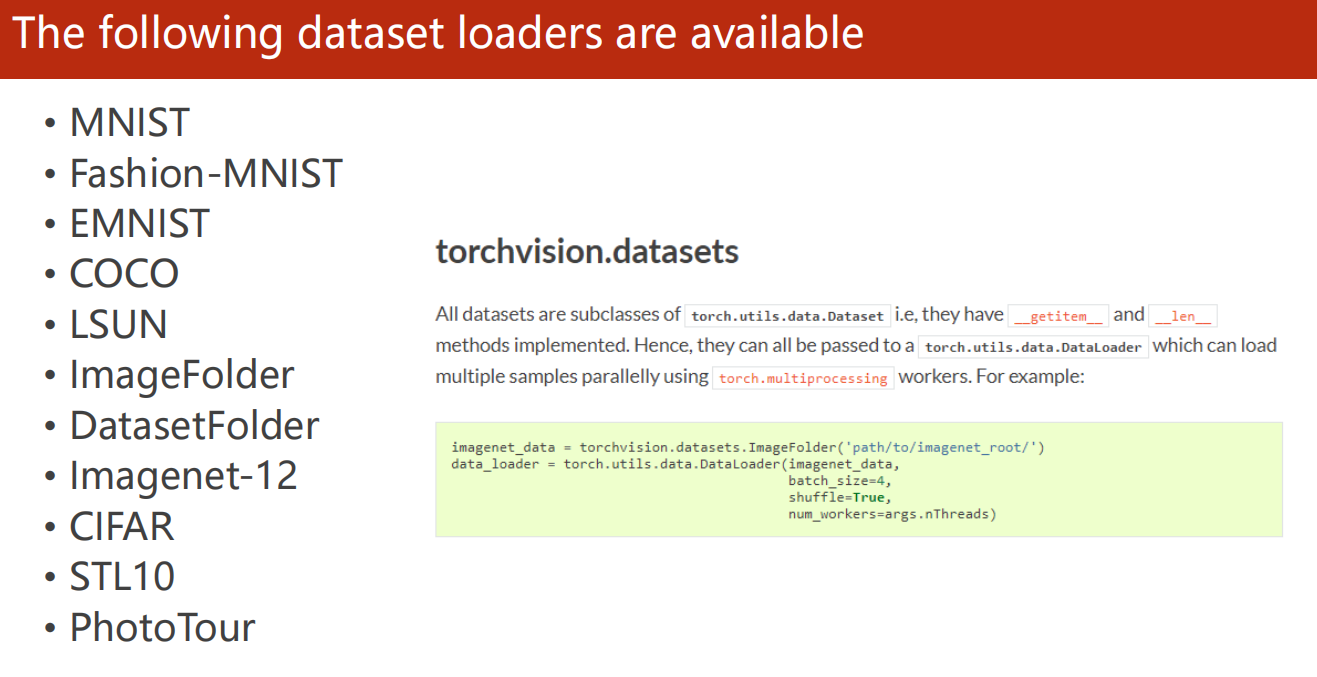
-
使用实例
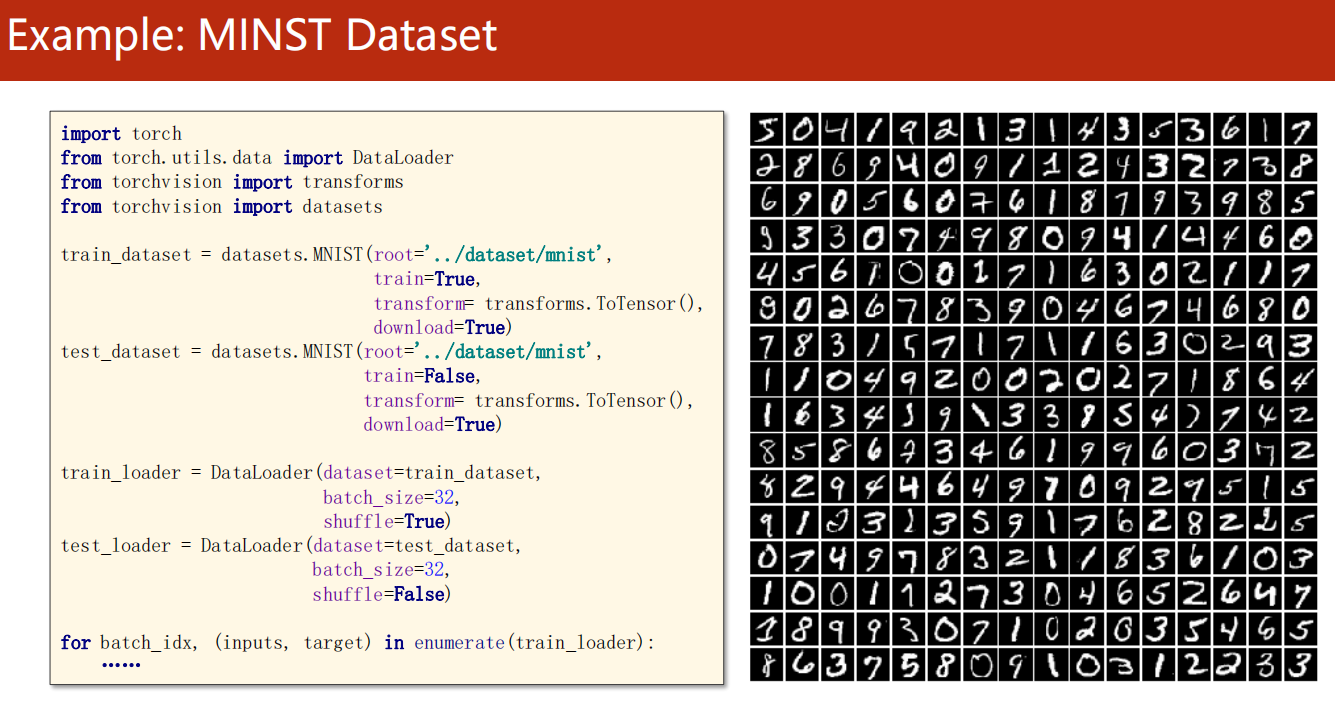
*8.5 课后题
09、Softmax Classifier
9.1 引入
-
对于糖尿病预测
只有两种可能:
- 患病
- 不患病
这是二分类问题。
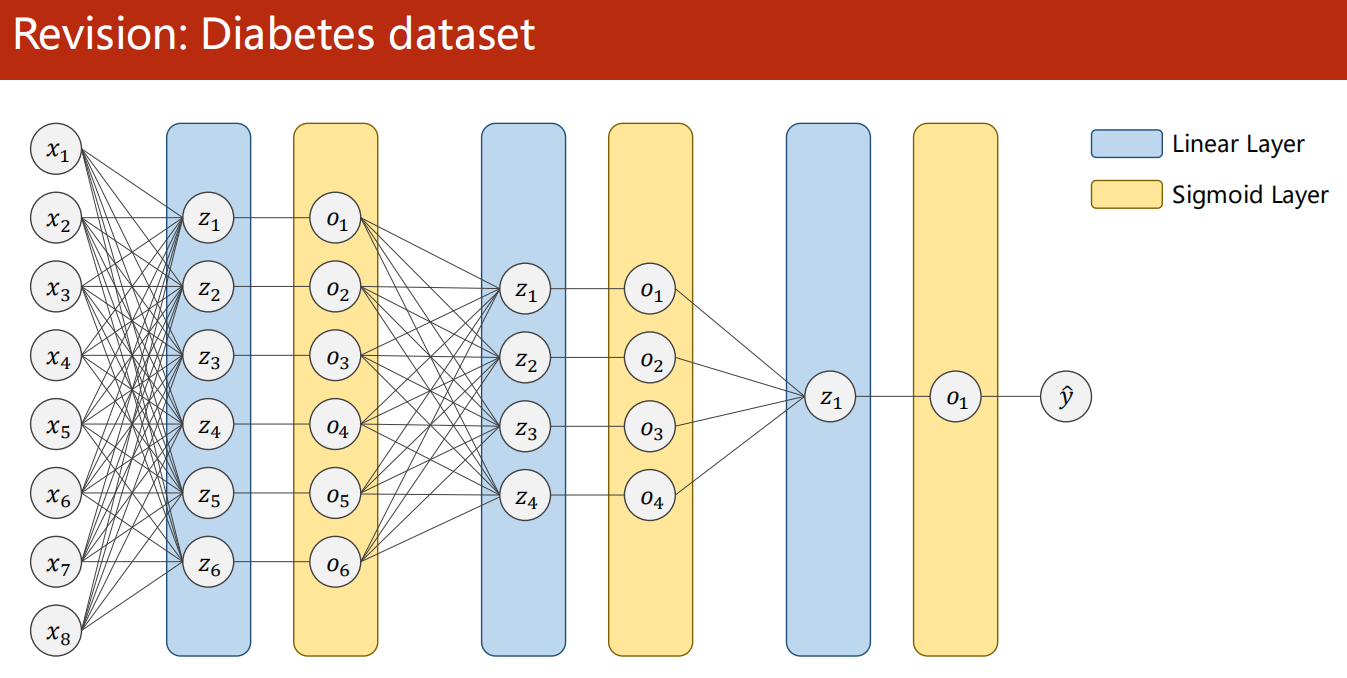
-
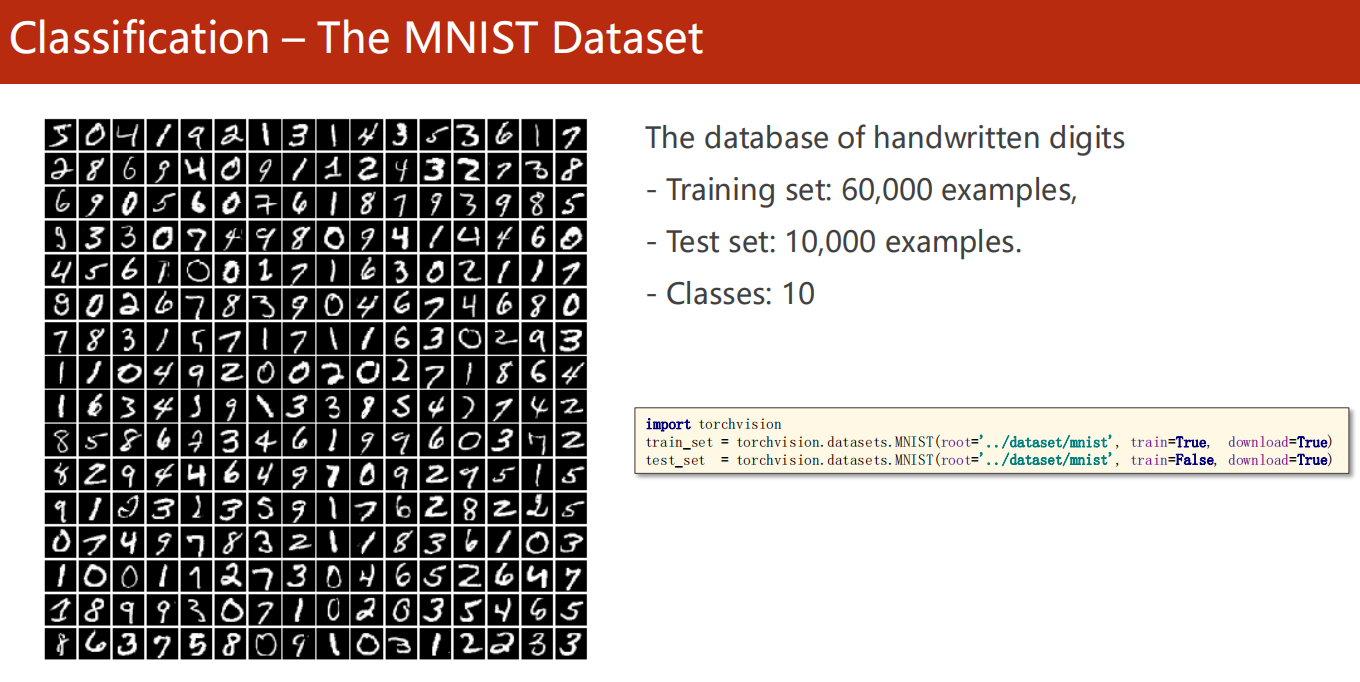
对于数字识别 MNIST 数据集
有 10 个类别,不再是二分类问题了。
如何设计神经网络?

-
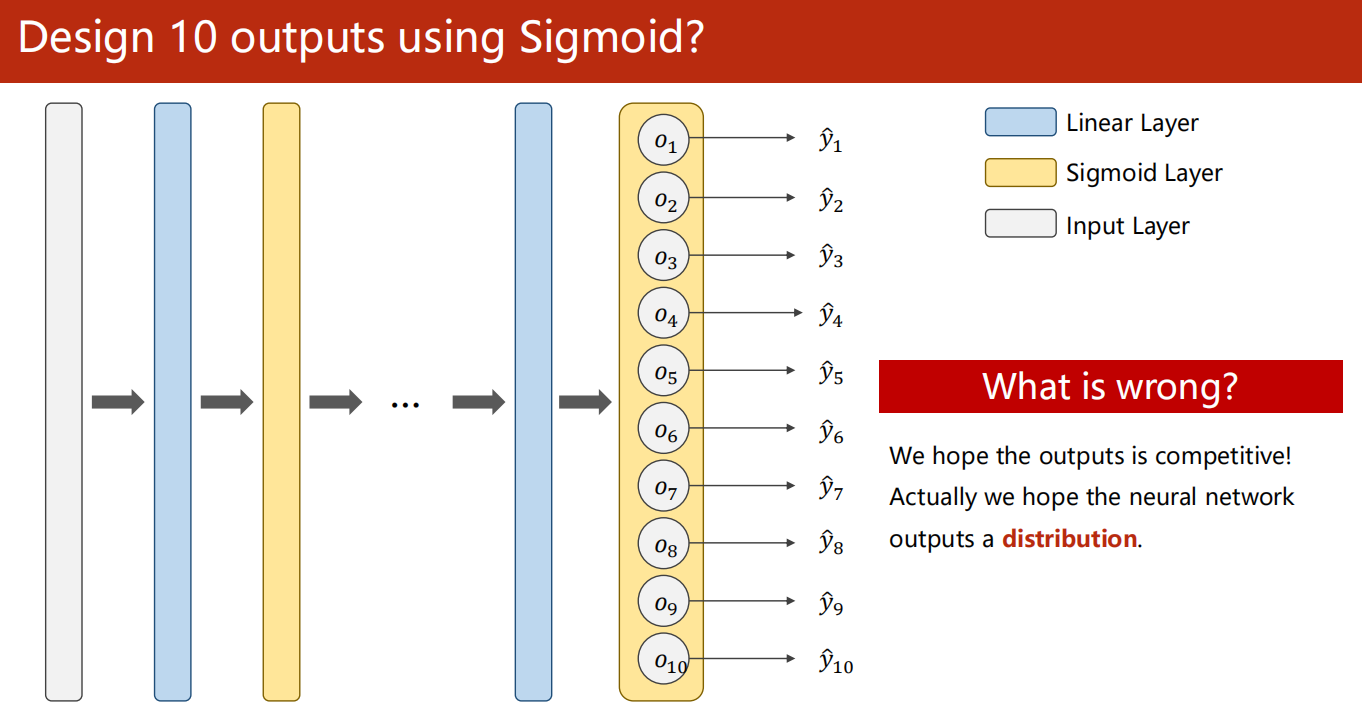
直接使用 sigmoid 控制 10 个输出吗?
这是不合理的,因为我们是希望同一个样本的10个输出应该是互相影响且是互相抑制的关系。
或者换句话说,我们希望输出是一个分布。
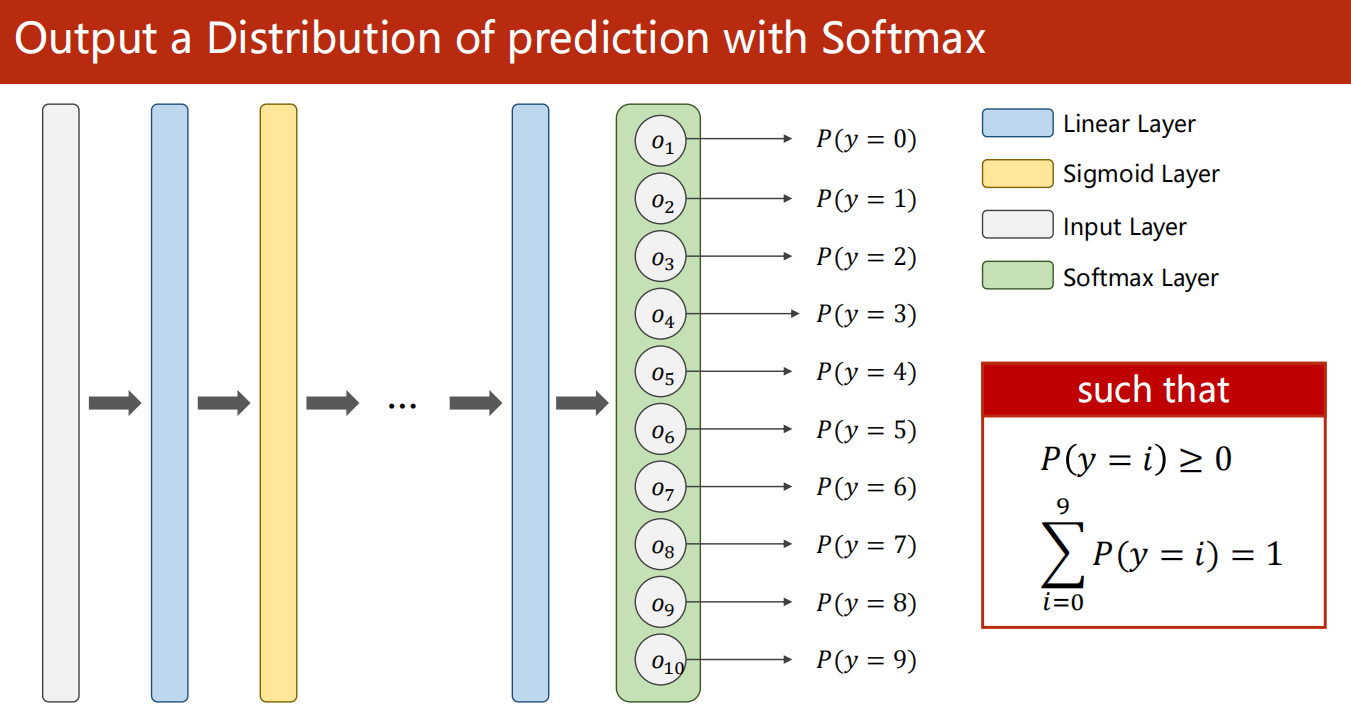
-
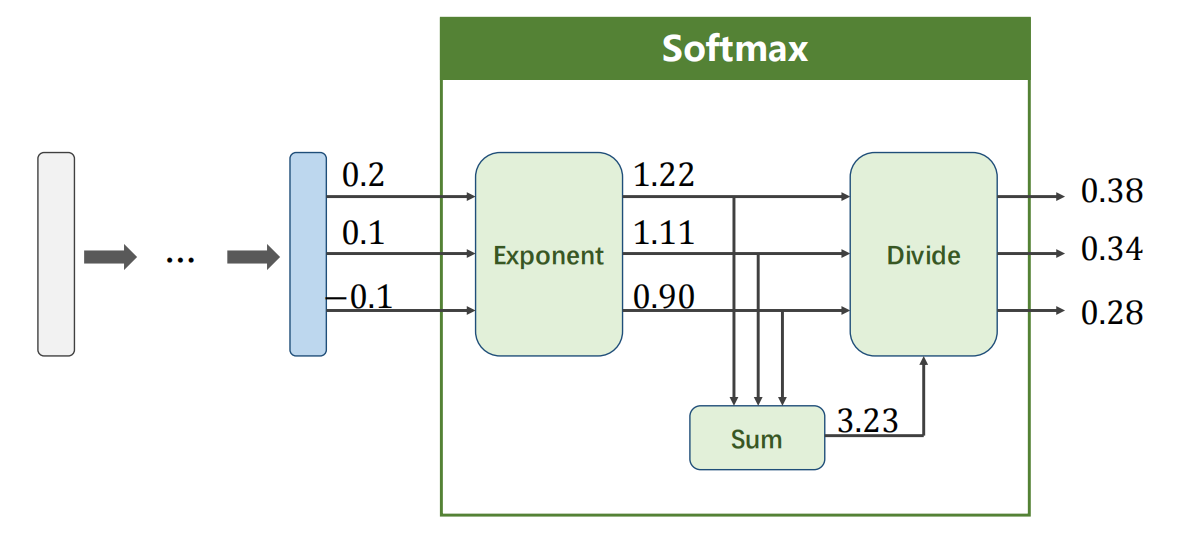
使用 Softmax 输出预测的分布
这 10 个输出都是一个概率。
且满足 概率均非负,且和为1。这符合概率分布的要求。
-
Softmax 函数
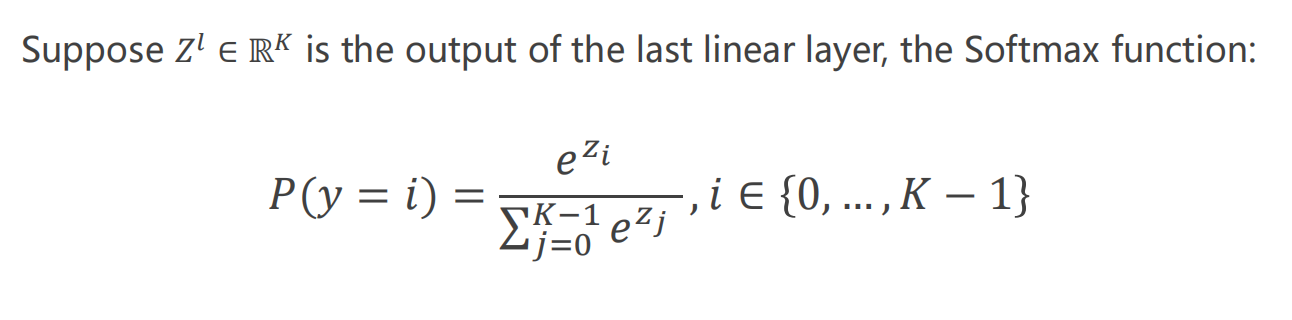
-
Softmax 层
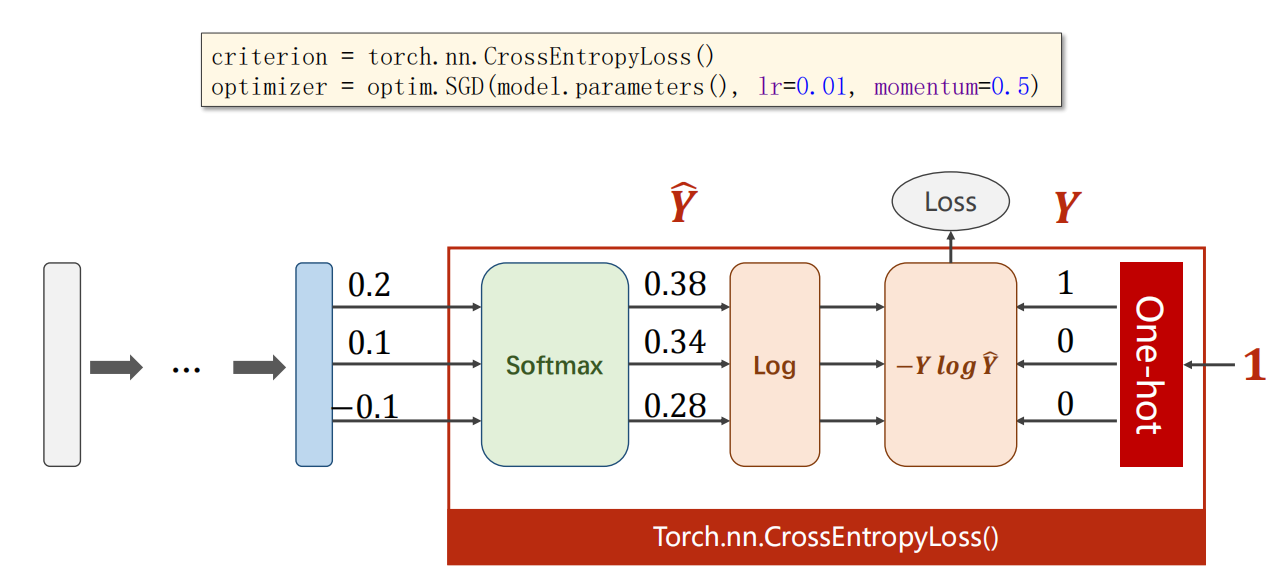
9.2 损失函数
-
NULLLoss
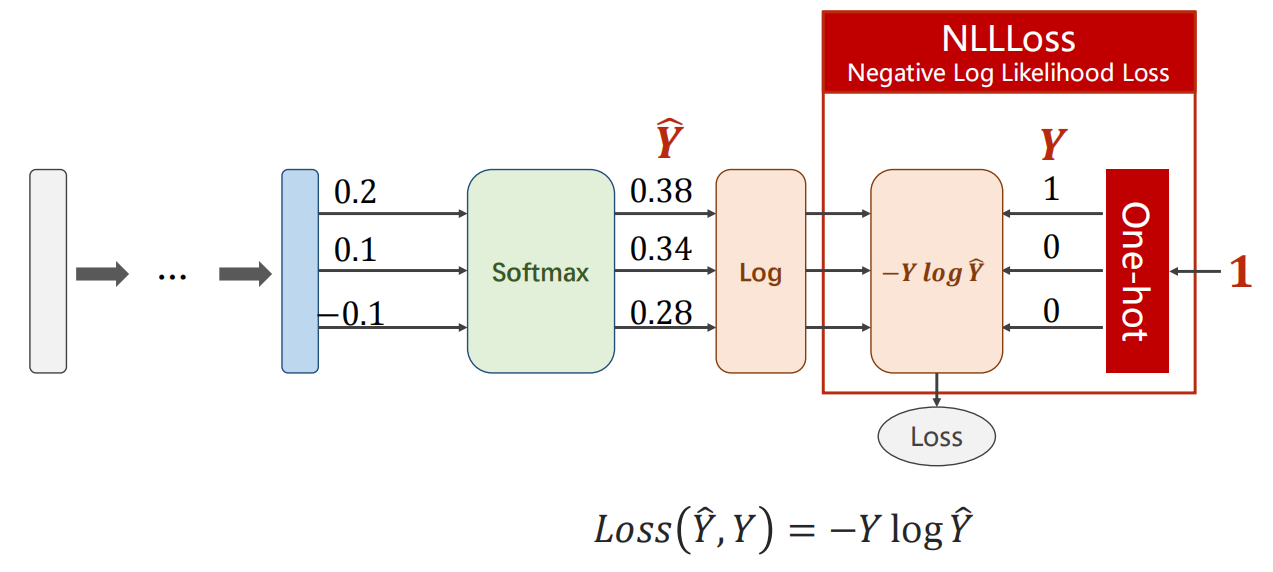
-
CrossEntropyLoss 交叉熵
可以直接把从 softmax 层往后都结合,这就是 一个 CrossEntropyLoss 层。
注:以下只能二选一
- 选用 ,则需要多添加前面的 并再求出 ,再和真实的 进行乘积得到 损失函数值。
- 选用 ,前面直接是激活函数 sigmoid 即可。
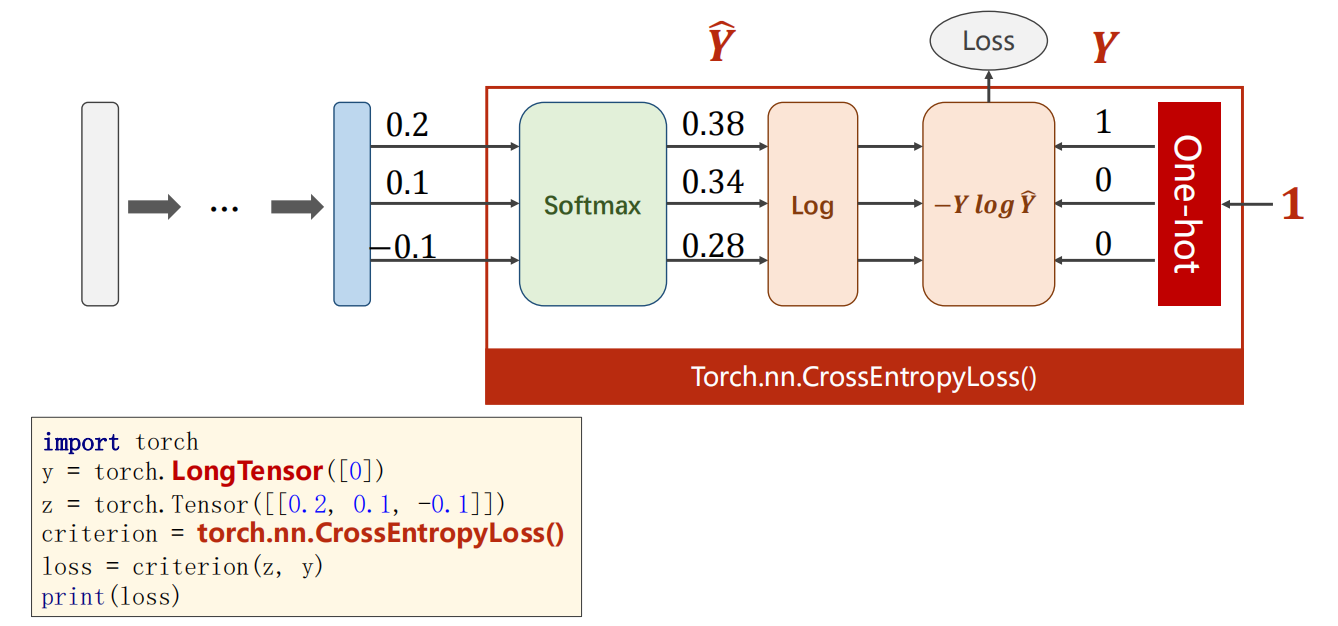
-
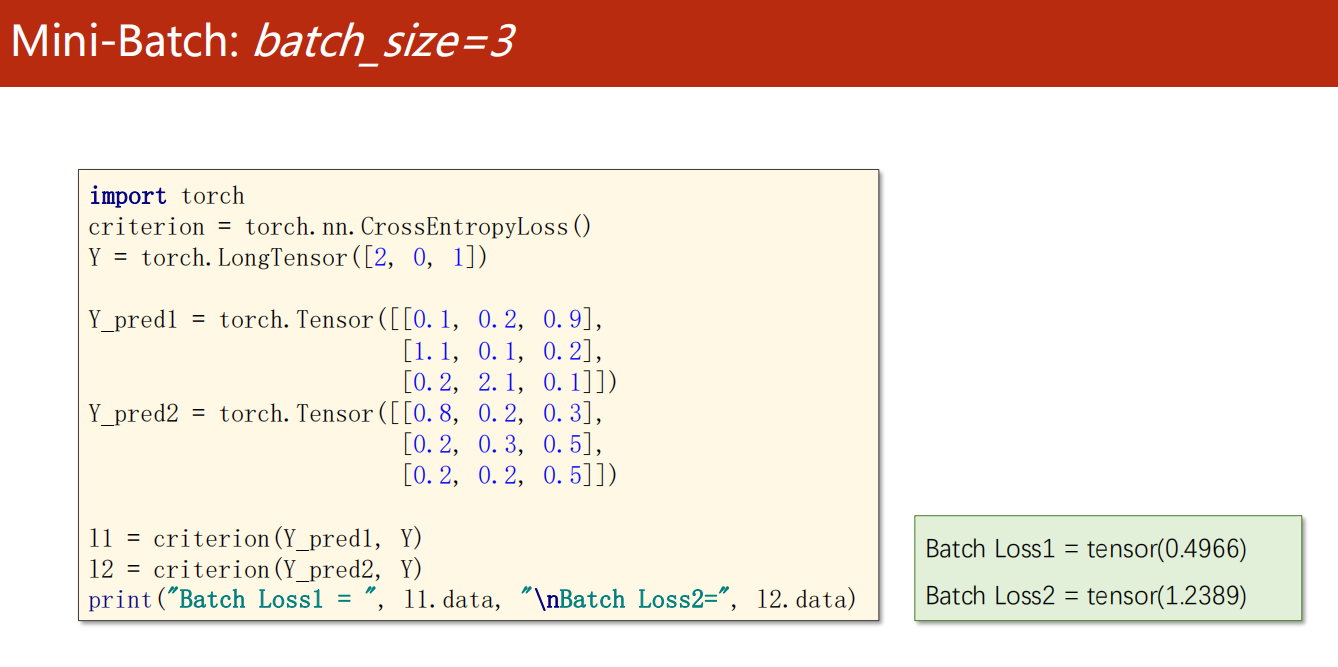
示例:使用 CrossEntropyLoss 交叉熵
可以看到,的确很有效地反映损失情况。
值越小,损失越小。
*9.3 练习1
-
Exercise 9-1: CrossEntropyLoss vs NLLLoss
-
两者有什么区别?
-
阅读:
-
尝试理解
9.4 示例:数字识别


-
仍然是基本流程
-
本次,我们需要使用到的注意点有:
- 激活函数采用 ReLU
- 使用 Dataset 和 Dataloader
- 使用图片作为输入(后面讲解)
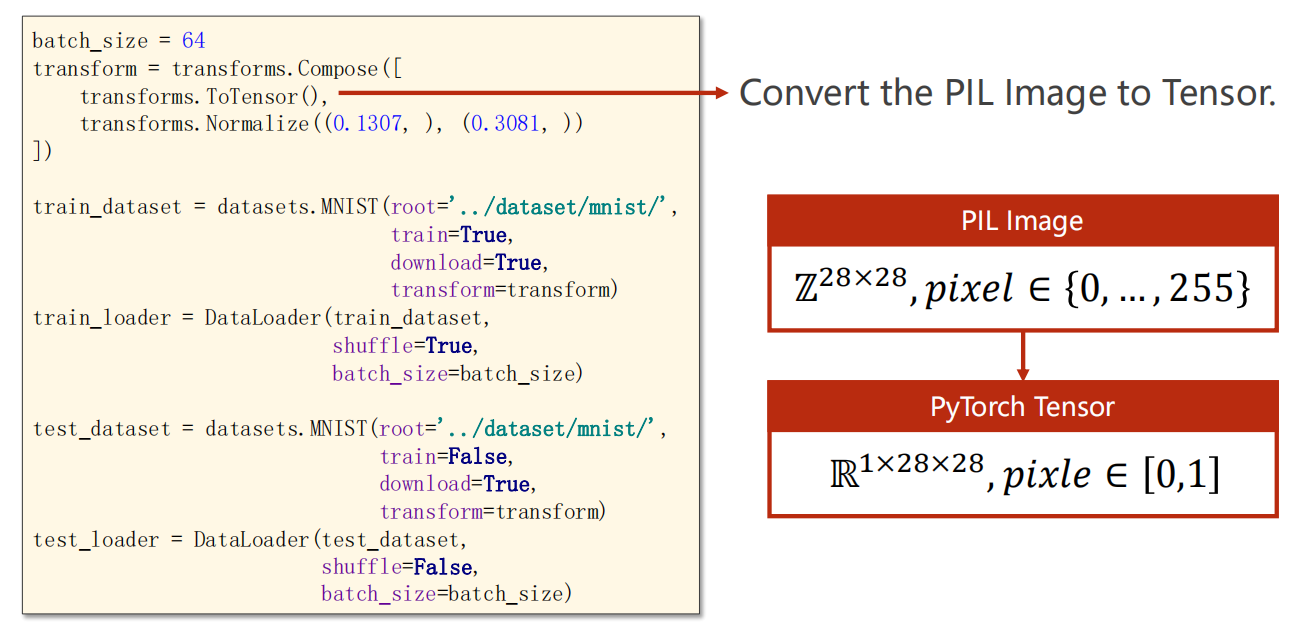
1、准备数据
-
图片输入问题:数值变换 transform
这里我们的一张照片是 28*28 = 784 个像素点,
每个像素点是的值 pixel 都是 0~255 中的一个整数。
因此,我们映射需要到 上。
为什么要映射到 上?
因为神经网络往往对 值域为 的分布有更好的学习能力。
-
如何映射?
按照概率论的分布理论,就是将分布标准化(归一化)
下图中的 和 怎么来的?
经验之谈,一般对于像素点值的均值和方差,就是这个值。
故采用这两个值来进行标准化。

2、设计模型

3、构建损失函数、优化器
4、训练轮次
-
train 训练

-
tets 测试
测试下是不需要计算梯度的。(因为不进行反向传播和优化)
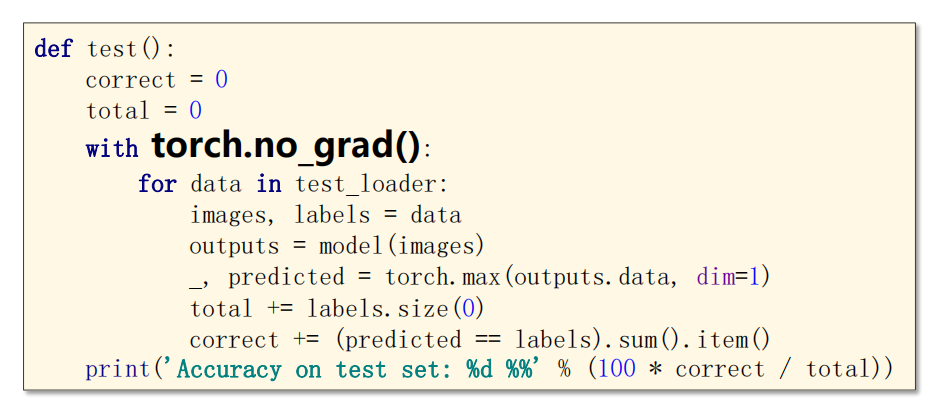
-
运行

9.5 代码实现
1 | import torch |
*9.6 练习2
-
Exercise 9-2: Classifier Implementation
-
尝试实现一个分类器
Otto Group Product Classification Challenge
10、Basic CNN
10.1 引入
-
回顾之前:全连接网络

-
本次需求:卷积神经网络
Convolutional Neural Network 卷积神经网络
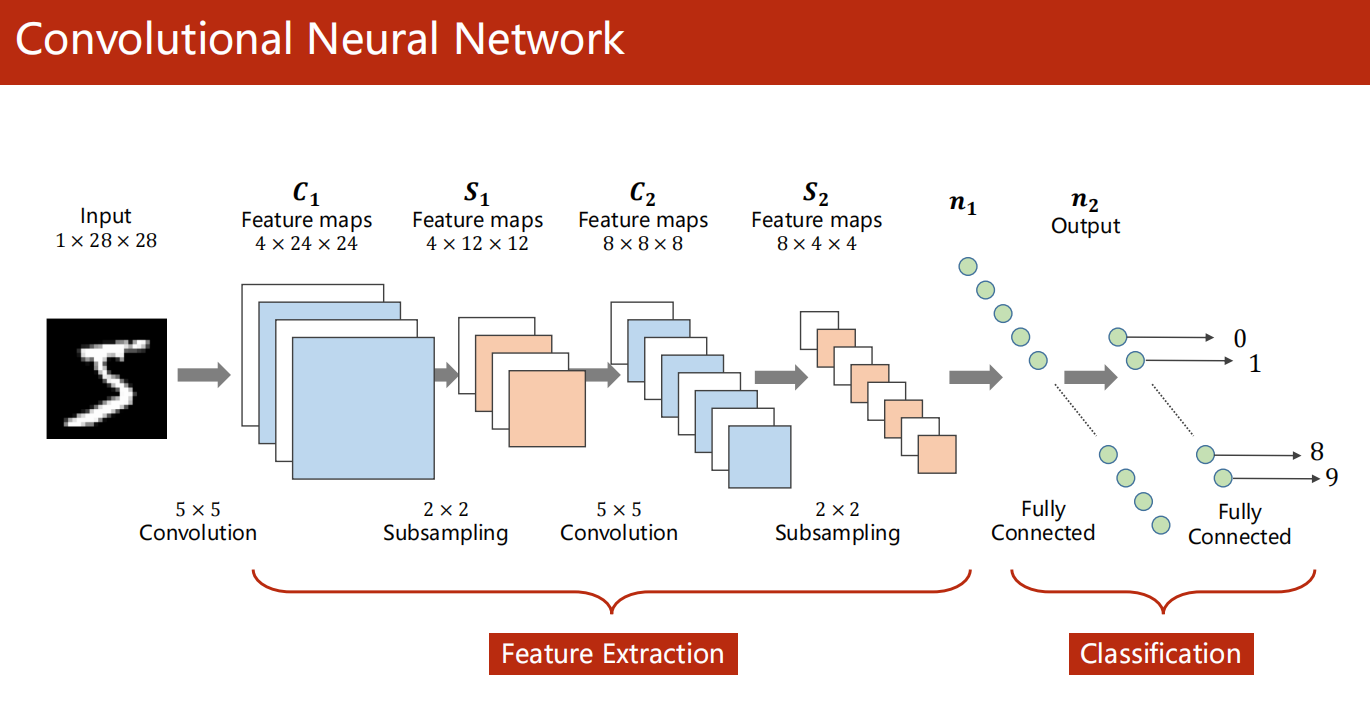
10.2 卷积
-
介绍卷积操作
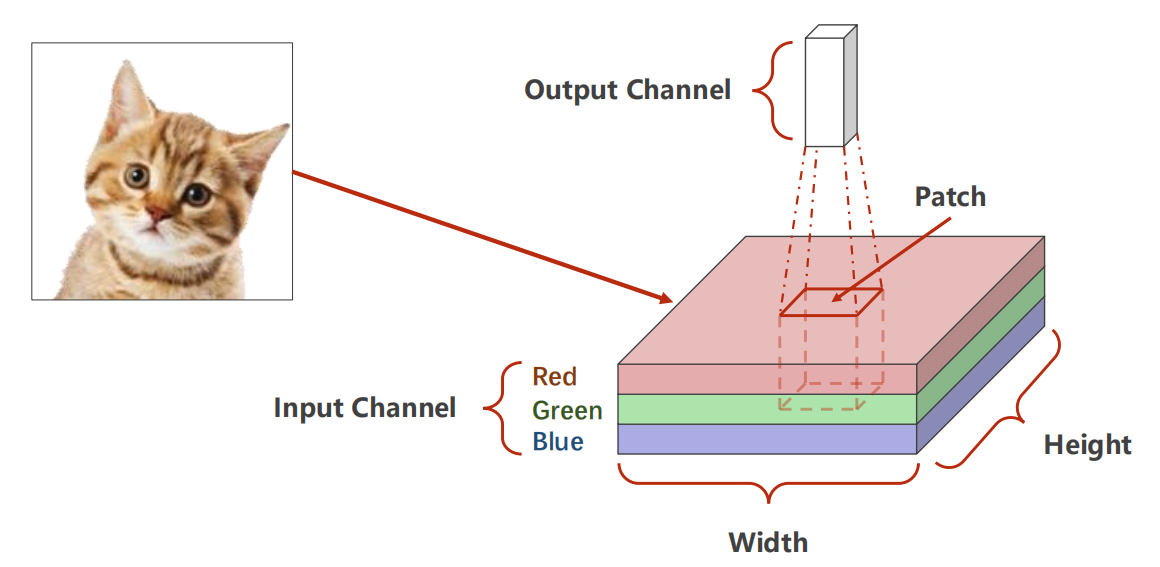
-
计算过程如下
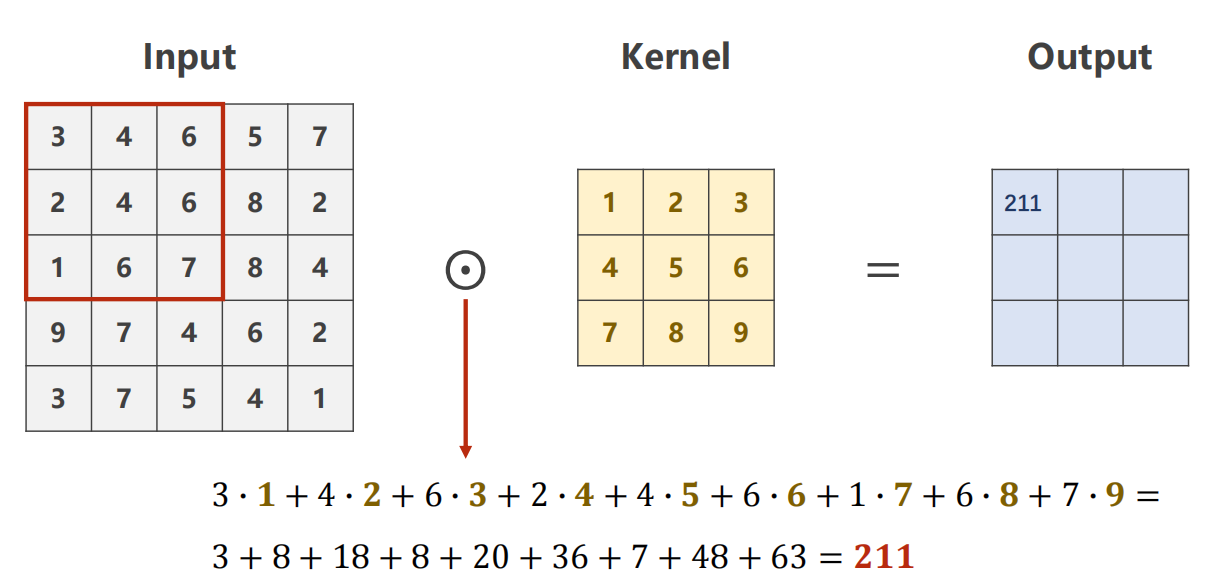
-
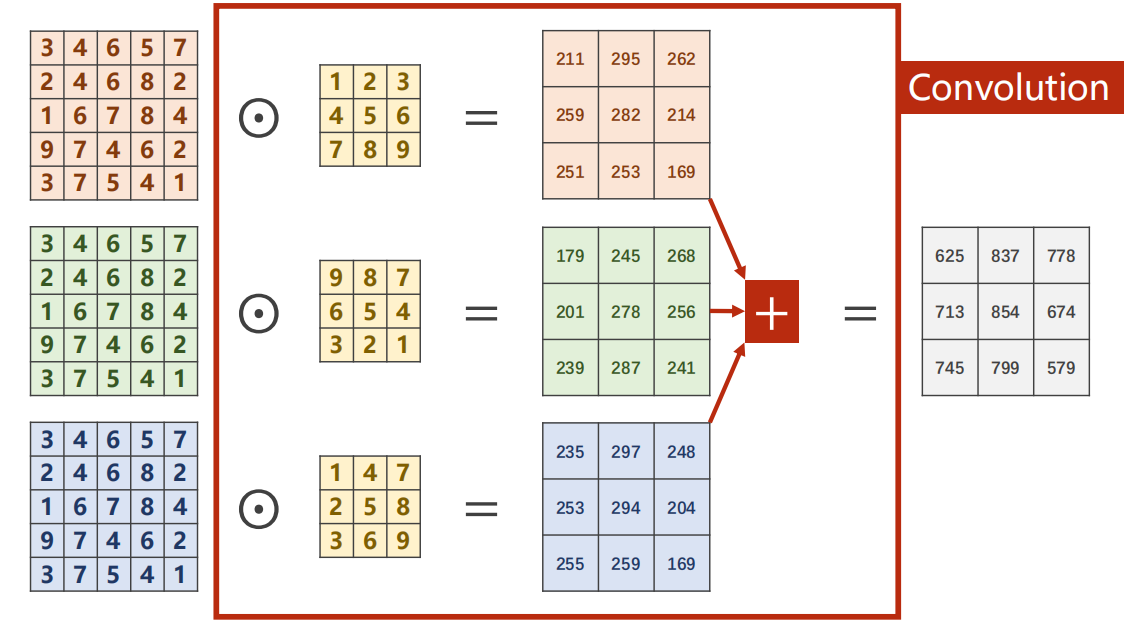
若输入为 三通道
计算过程:
- 架构情况:
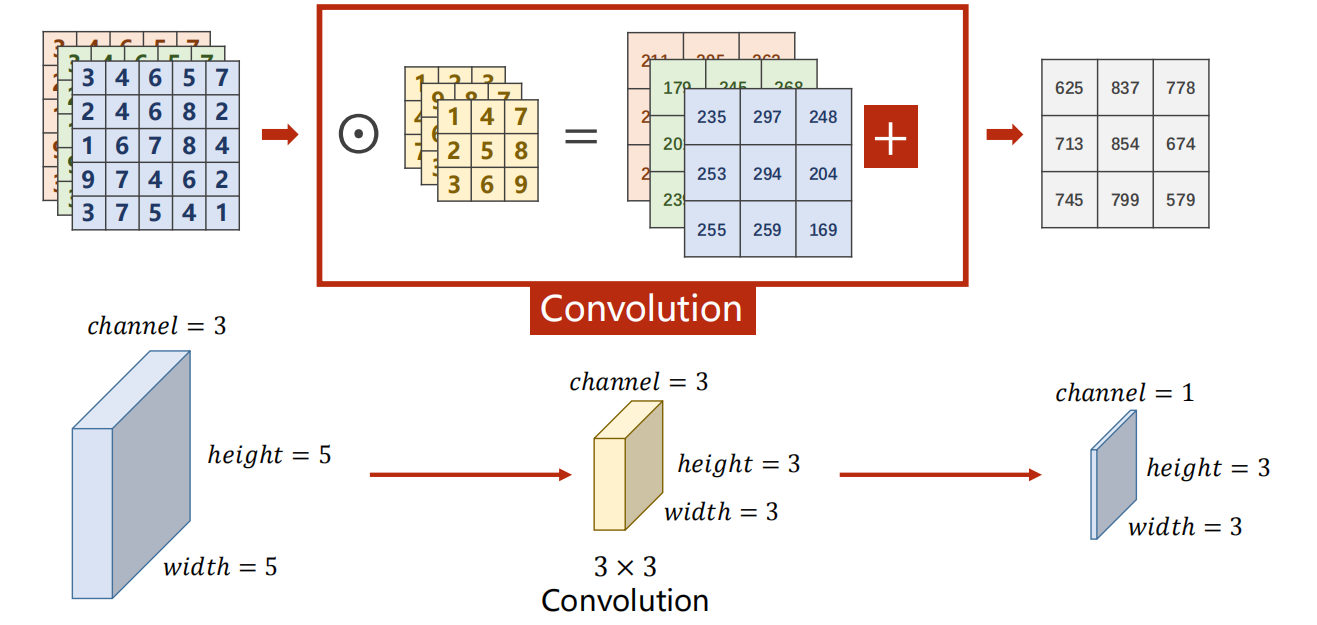
-
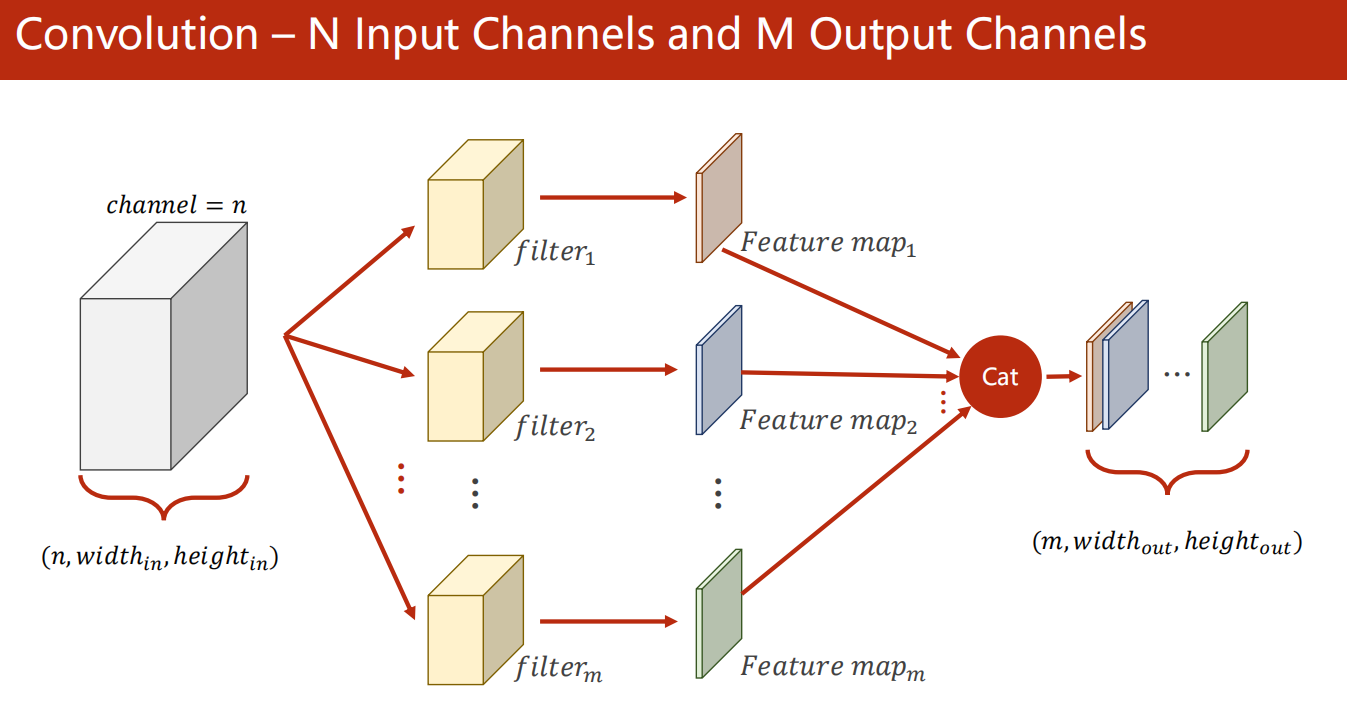
输入 N 通道,输出 M 通道
做法是:
- 做 M 次如下的 filter 卷积(每次的 filter1不一样,即 kernel 不一样)
- 每一次的 filter 卷积都是一次 N 通道输入,1 通道输出。(即前面的方法)
- 得到的所有 结果,在 channel 维度上连接 起来即可。
具体代码做法如下:


10.3 卷积参数
-
padding 外框
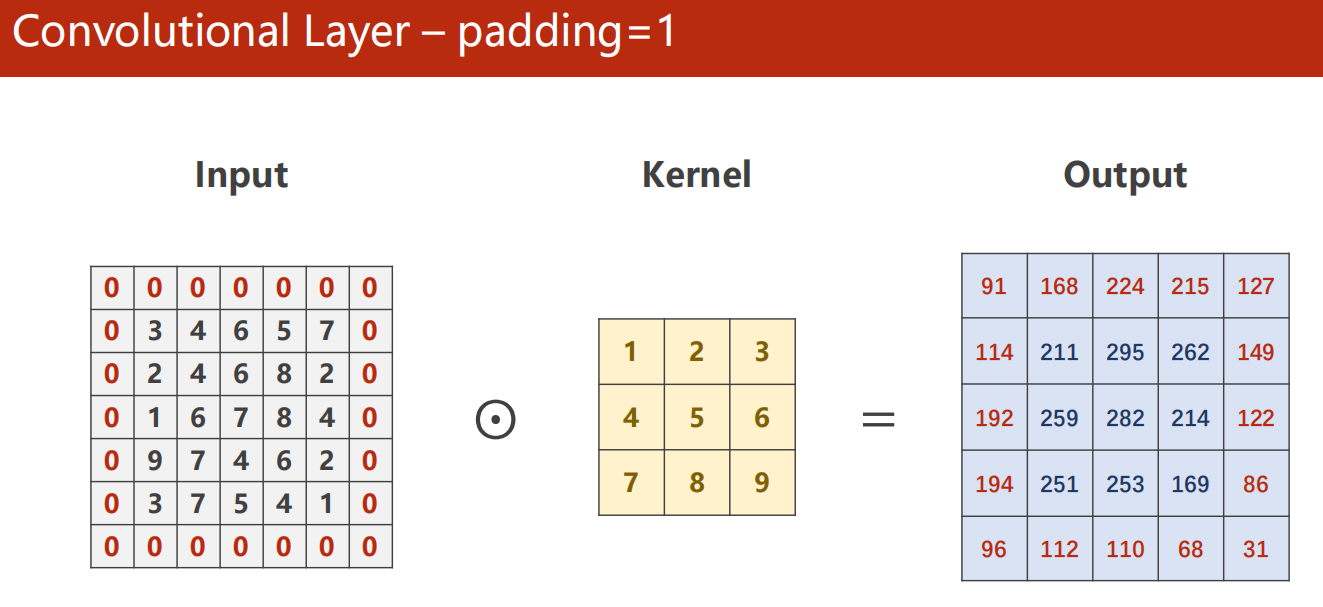

-
stride 步长
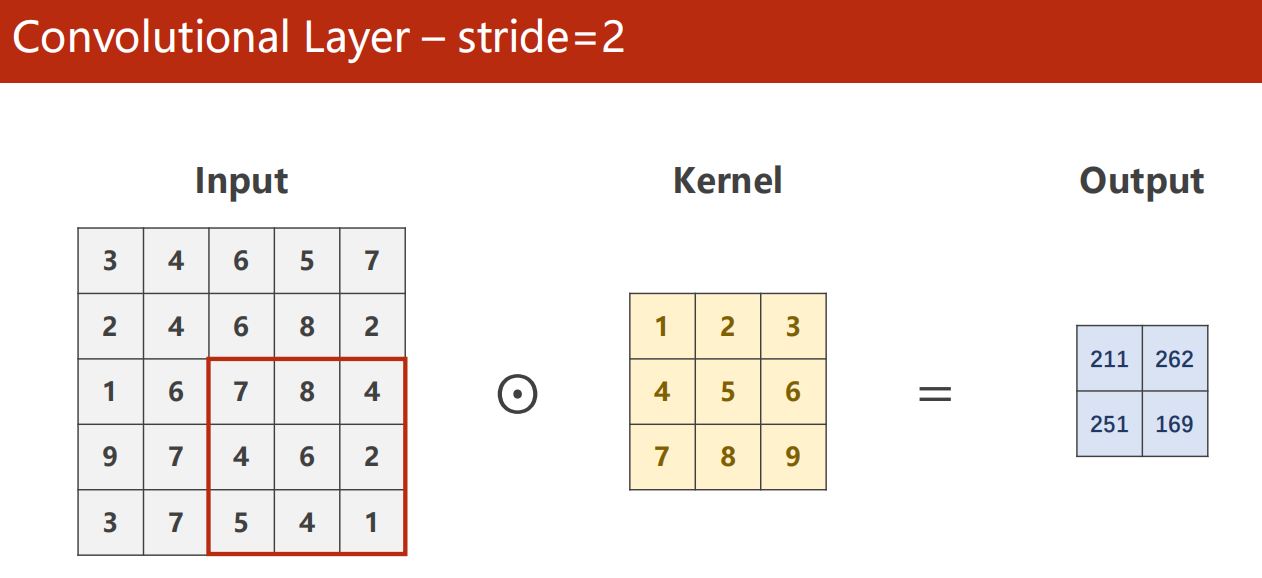

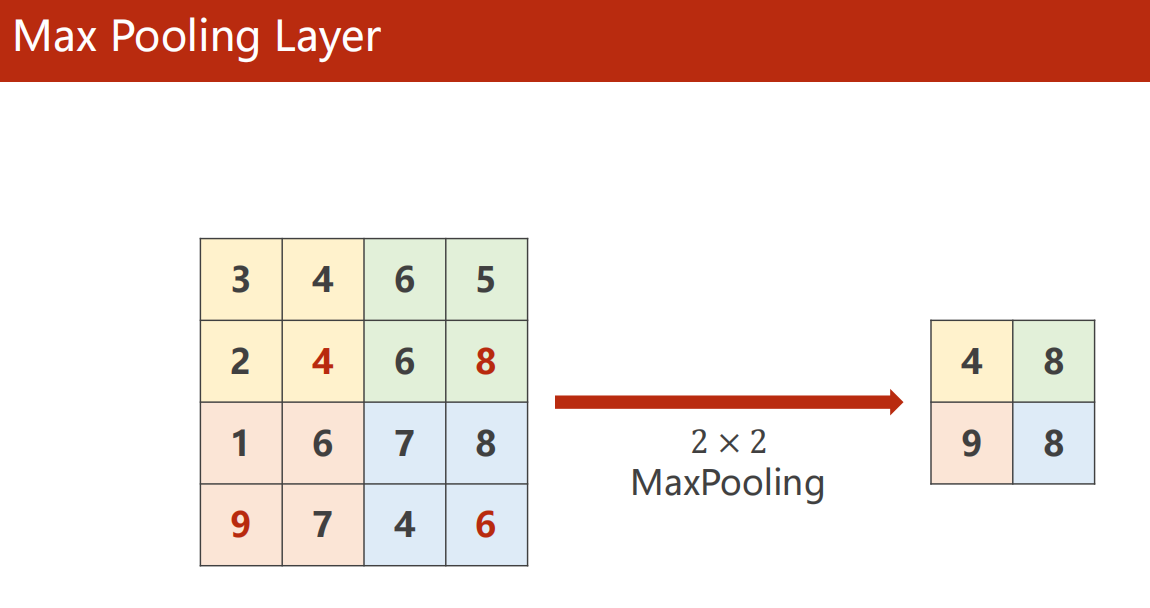
10.4 Max Pool 最大池化

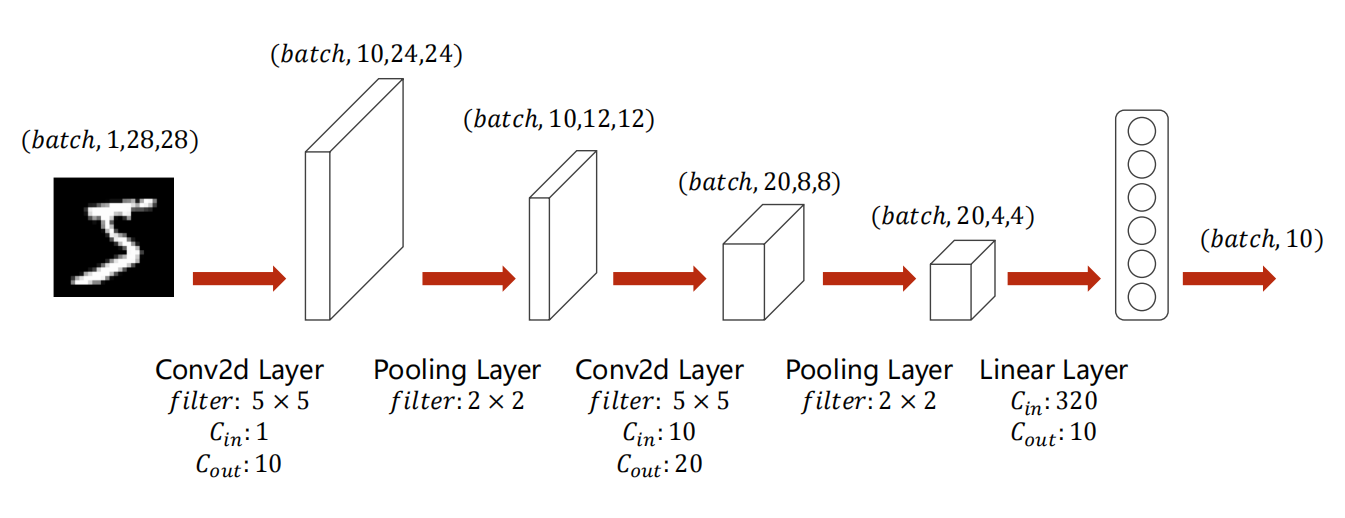
10.5 示例:数字识别

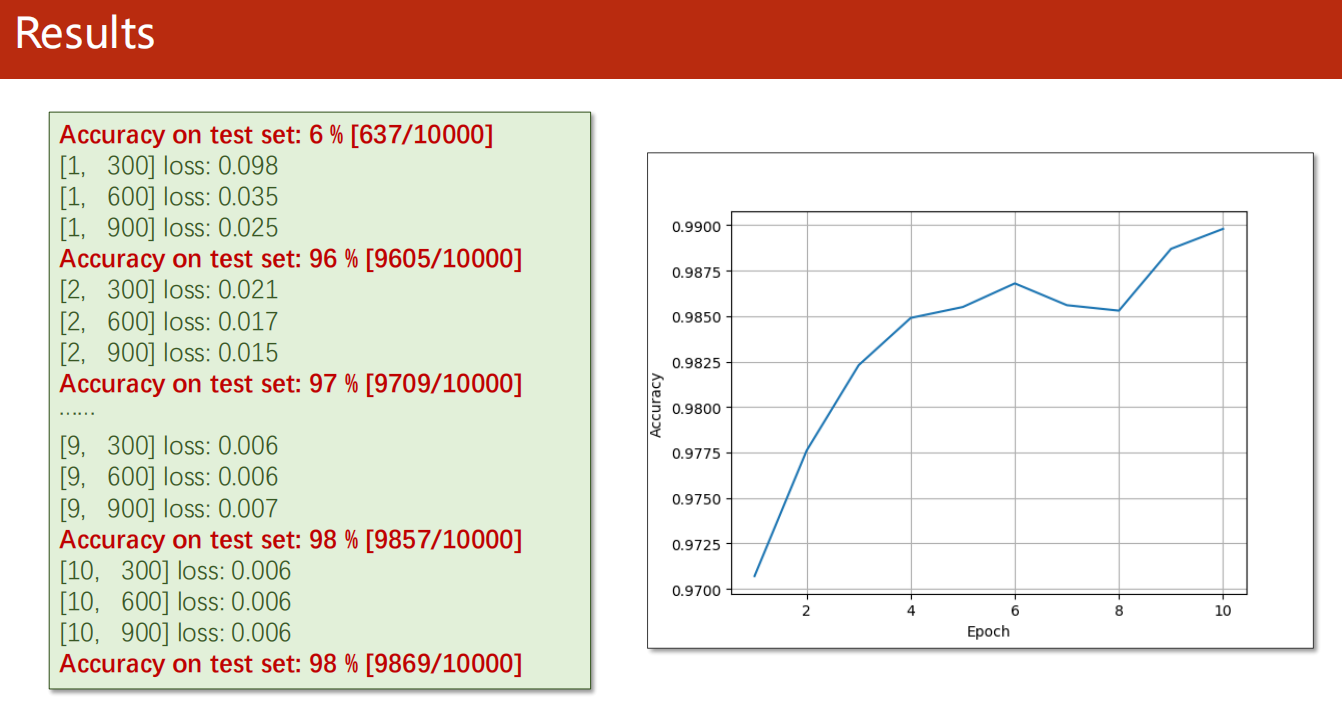
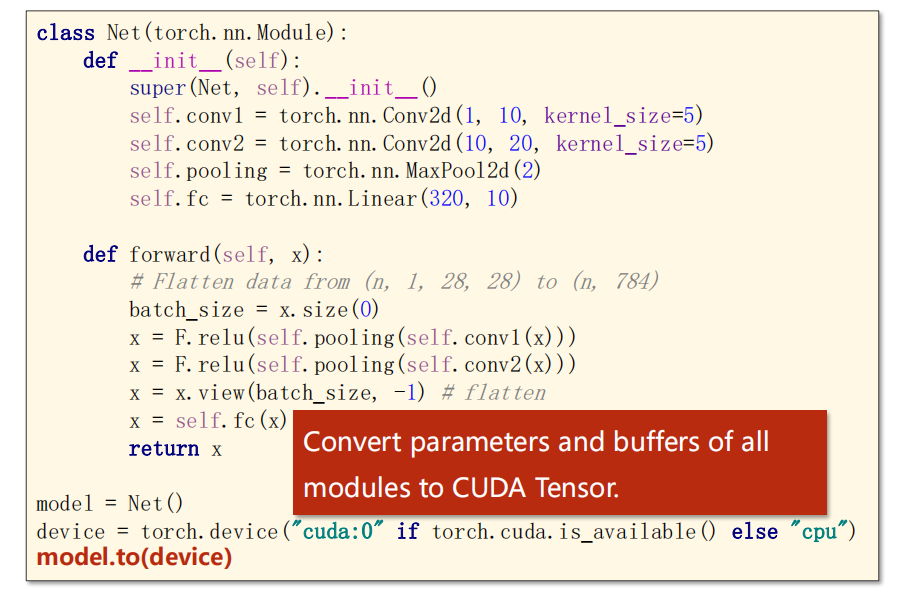
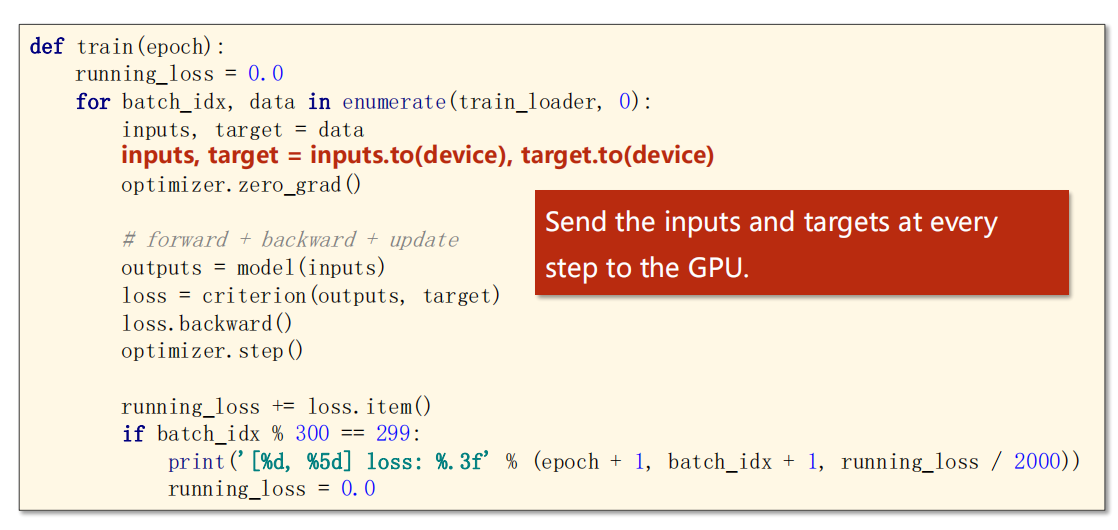
*10.6 使用GPU
-
代码仍然不变
只需要加上一些内容即可
-
添加
- 定义 CPU 设备
- 将 model 移动到 GPU 上计算
- 将训练的数据输入输出 inputs、outputs 移动到 GPU 上

*10.7 练习
-
Exercise 10-1: Try a more complex CNN / Try a more complex CNN
- 设计一个更复杂的卷积神经网络
- 3个卷积层
- 3个非线性激活层
- 3个最大池化层
- 3个线性层
- 比较不同卷积神经网络的性能

11、Advanced CNN
11.1 引入
-
复杂的卷积神经网络,如下图的 GoogLeNet
层次很多,但是会发现,有一些结构是相同的!
这样有两个好处:
- 减少代码冗余,提高代码复用性
- 代码可读性提高,后期修改更方便
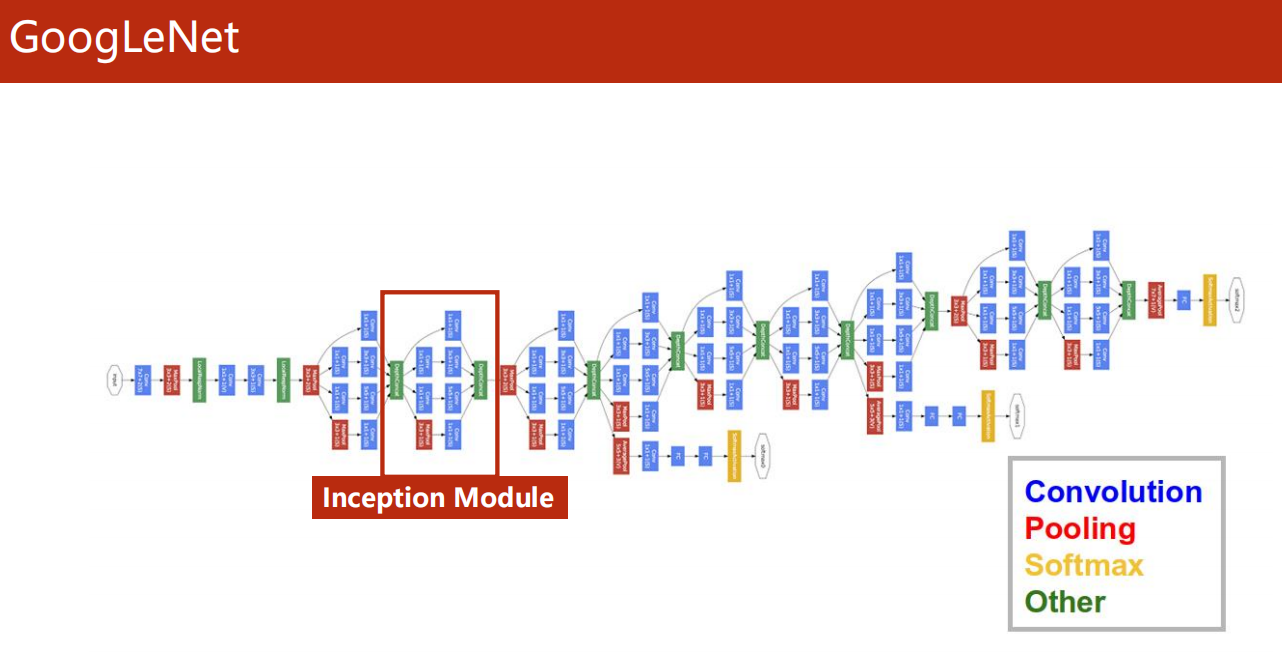
-
Incetion Modulde
如盗梦空间一样,这里的重复相同的结构,
我们把他看作是神经网络中的神经网络,一般叫做 Inception Module 。
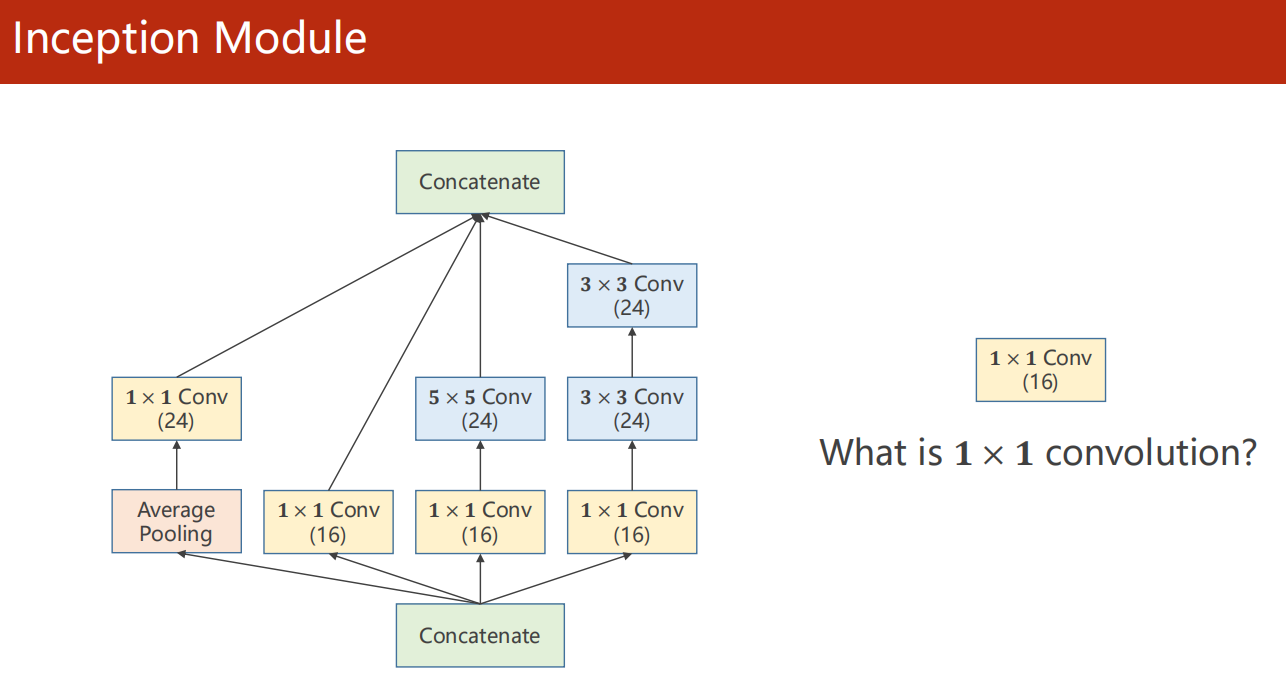
11.2 1x1 卷积
-
为什么会需要 1x1 的卷积?有什么效果?
-
计算过程
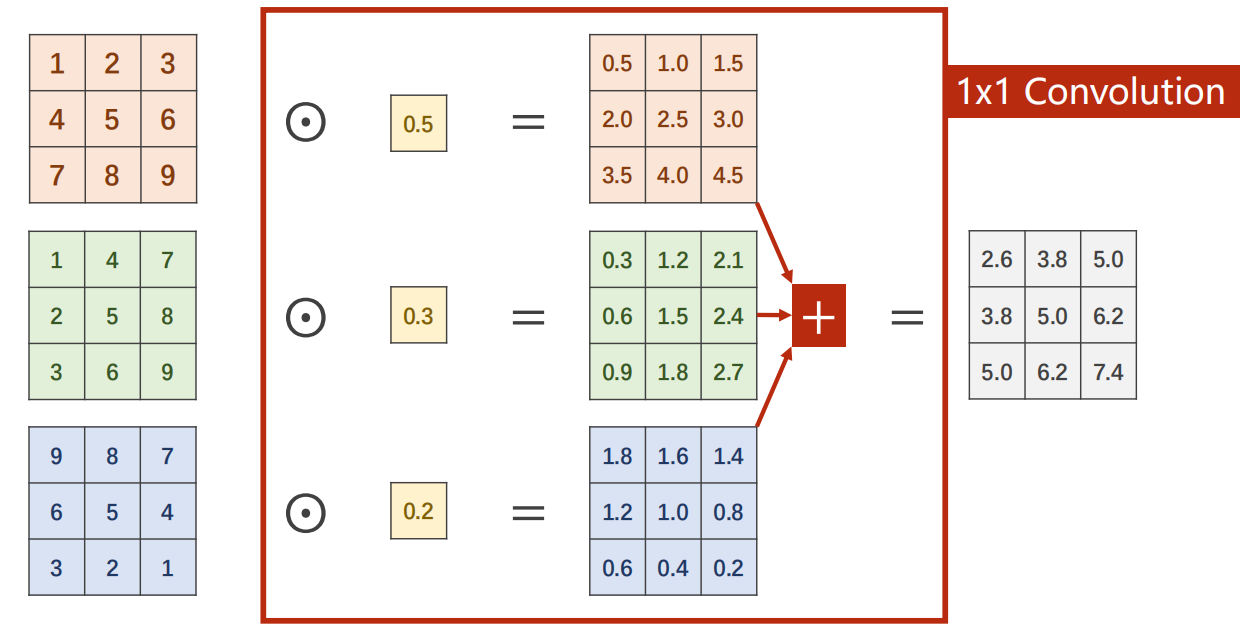
-
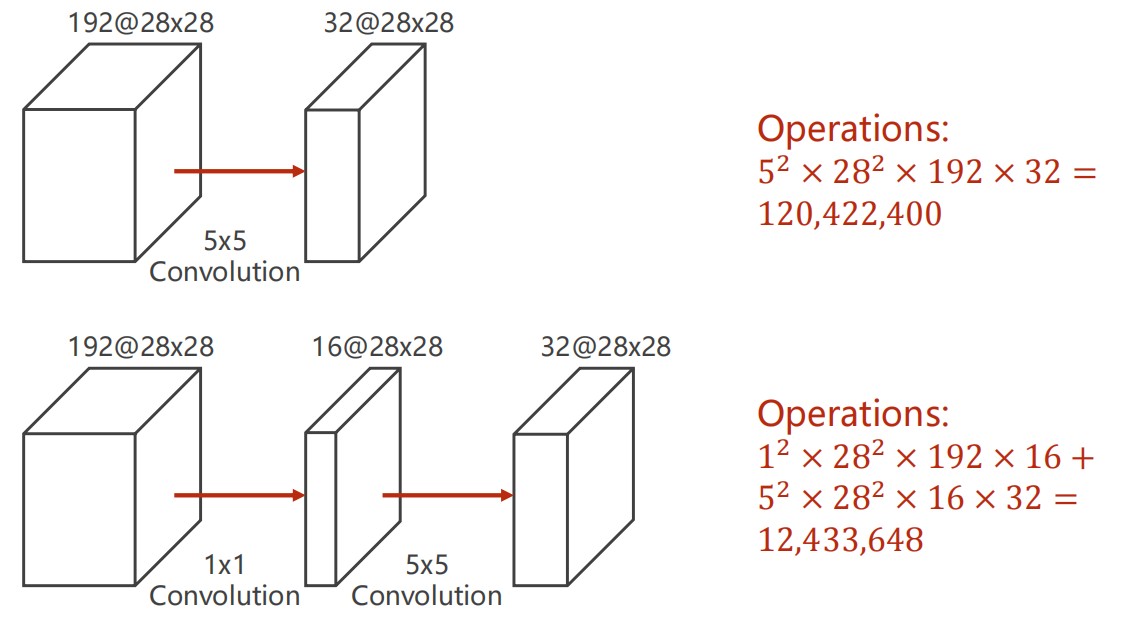
对比时间复杂度
卷积神经网络往往对于计算需求很高,这也是当前的一个难点。
因此,若能降低计算次数,但是达到几乎相同的效果,那当然是最好的。
对比下面 使用与不使用 1x1卷积的相同输入输出结构,计算次数降低到了 1/10。
11.3 Inception Module
- 继续说,这个神经网络中的神经网络 Inception Module
我的思考:它在做什么?意义何在?
从图可以看出来,它在并行的计算4种不一样的神经网络架构,最后把4种结构连接起来。
仔细思考,神经网络本身是做什么的?神经网络本质上是在寻找使得损失函数最小的参数。
所以说,只要是涉及参数的问题,在理论上来说,都是可以交给神经网络自己去学习的。
但是,模型定义是你做的呀!你怎么在训练之前就能知道定义什么样的卷积神经网络呢?(即,你怎么知道该使用多大的 kernel 呢?)
回过头来,你再看这个 Inception Module
实际上,它就是希望神经网络自己去找到最好的 合适大小的 kernel。
而我们是把不同的 kernel 并行的交给了它,最后合并,而这个合并的过程,就是它在自己学习到最好的 kernel (因为 1x1 卷积本身是有权值的)
架构分析
-
整体流程图
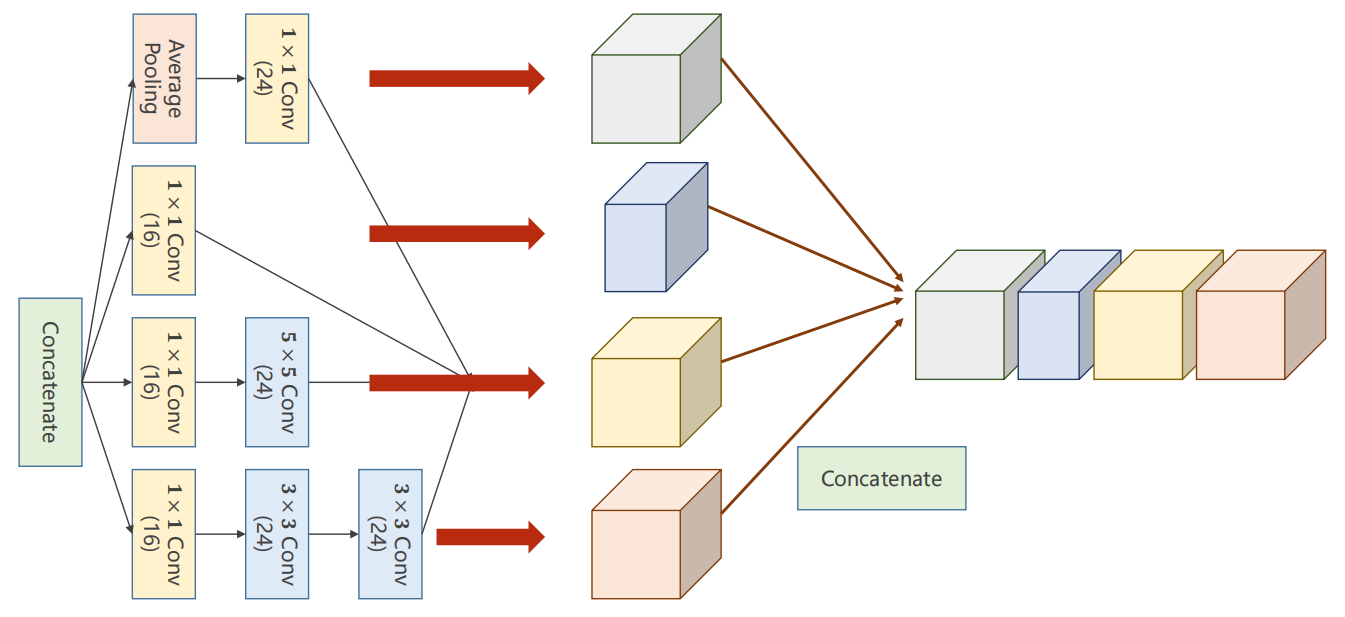
-
1:并行计算
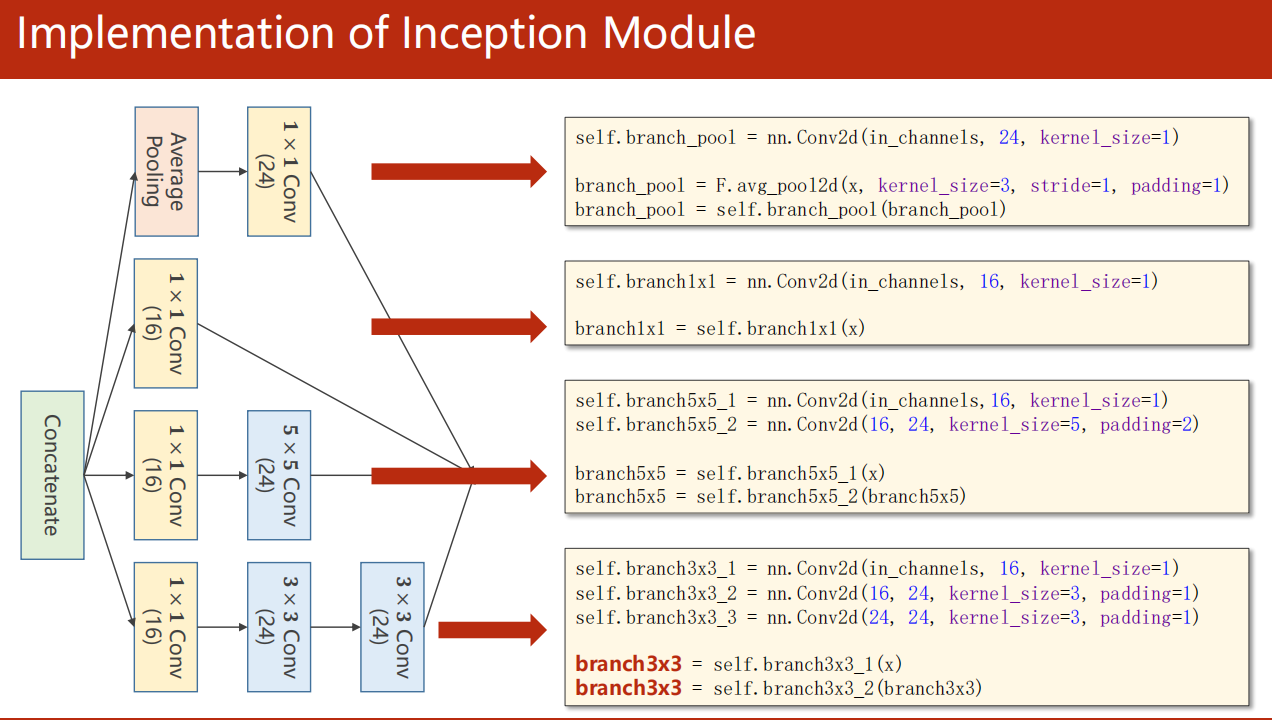
-
2:连接合并
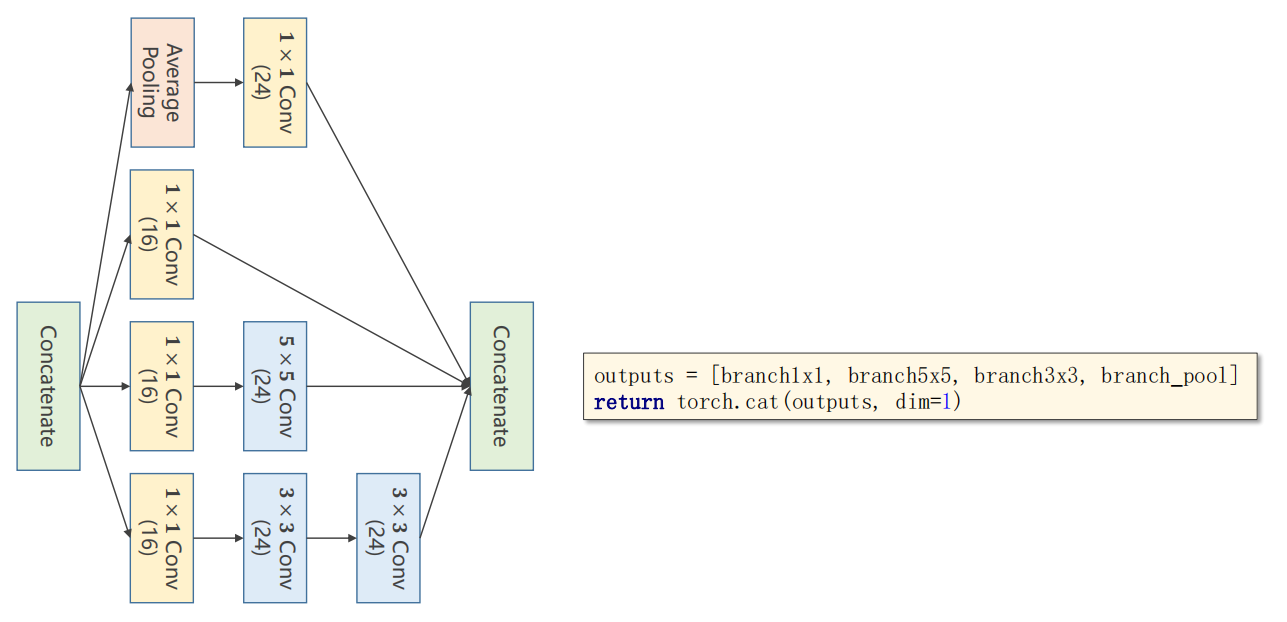
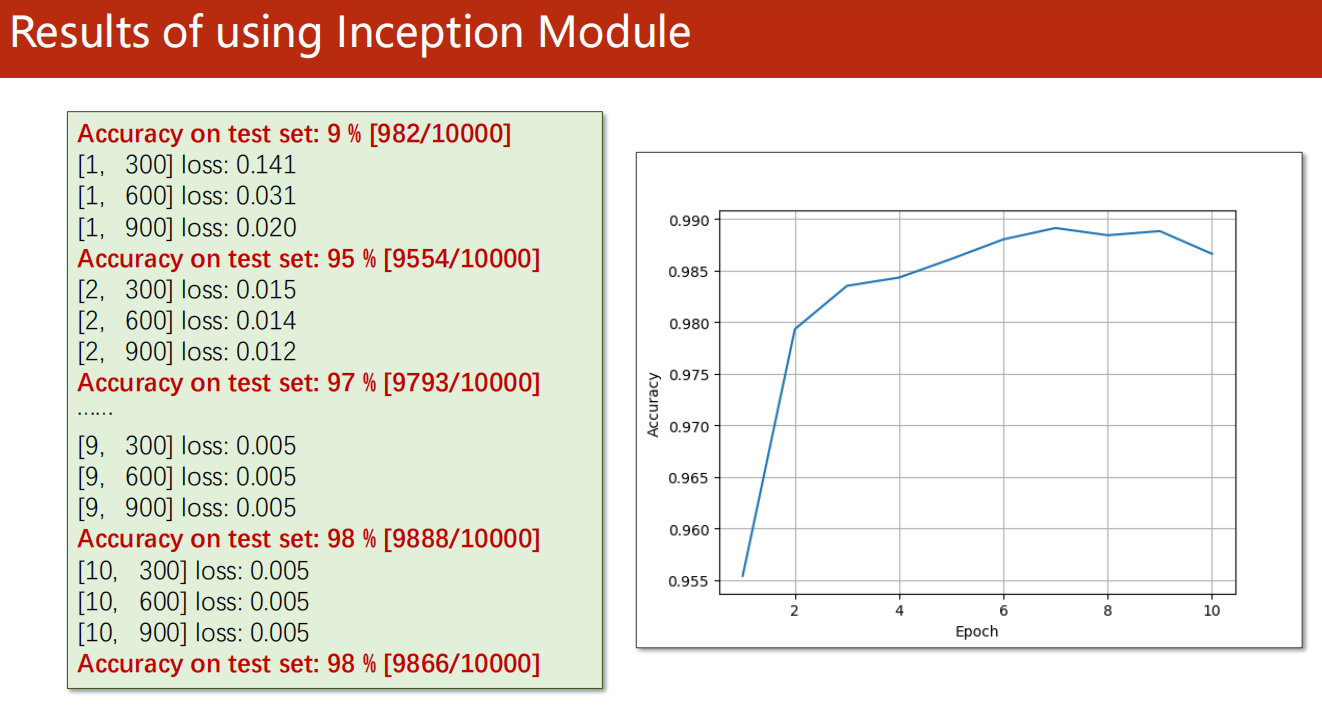
代码使用

结果
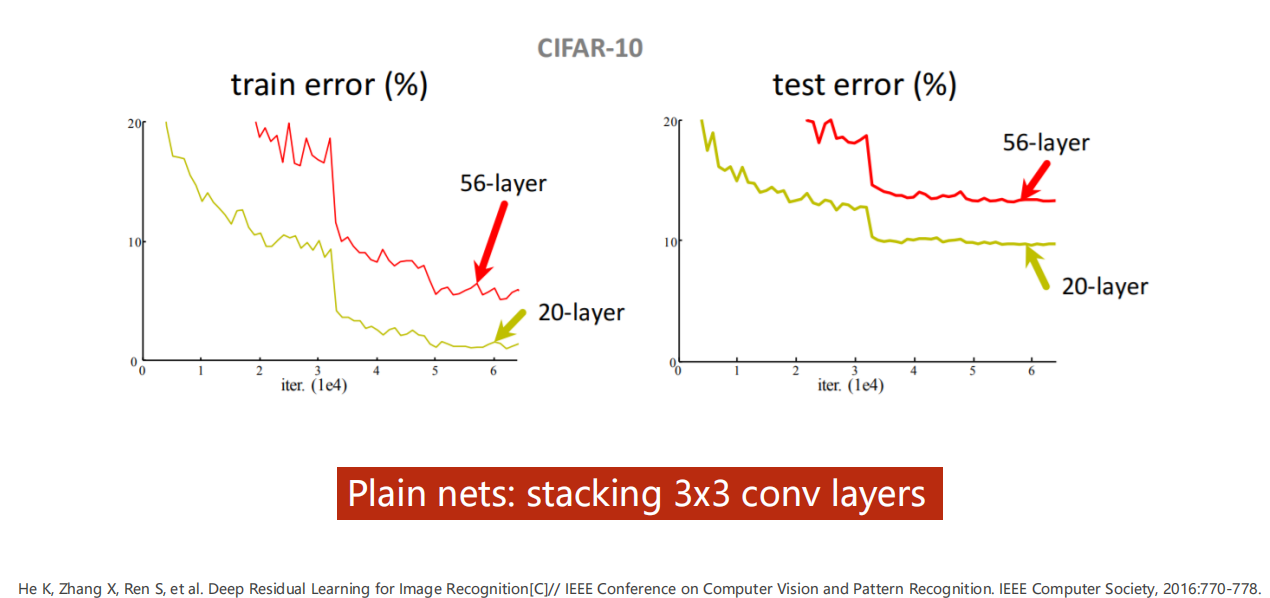
11.4 更深!
-
按照一般逻辑来看,
当神经网络越深(层次更多),那么对数据的处理细节会更多,自然应该更能达到高效损失地贴合数据。

-
但是,事实上
白部署完全遵循这个逻辑的,如下图。
实际上,你学的太好了,反而可能是把噪声也学进去了——过拟合。
图中底部文字:
11.5 Residual Net
原理
-
残差块 解决 梯度消失 问题
我们知道,虽然 梯度下降 算法在应用中实际上并不会存在局部与全局最优点的问题。
但是,梯度消失问题的存在的。
(梯度近乎为0,导致卡在该点无法行动。前面我们的方案是采用SGD,期望噪声帮我们跃迁过去。)
-
这里,我们采用在输出之后,在非线性激活之前,直接加一个输入 x 。
这样子,梯度由围绕0改为了围绕1,自然不会有梯度消失。
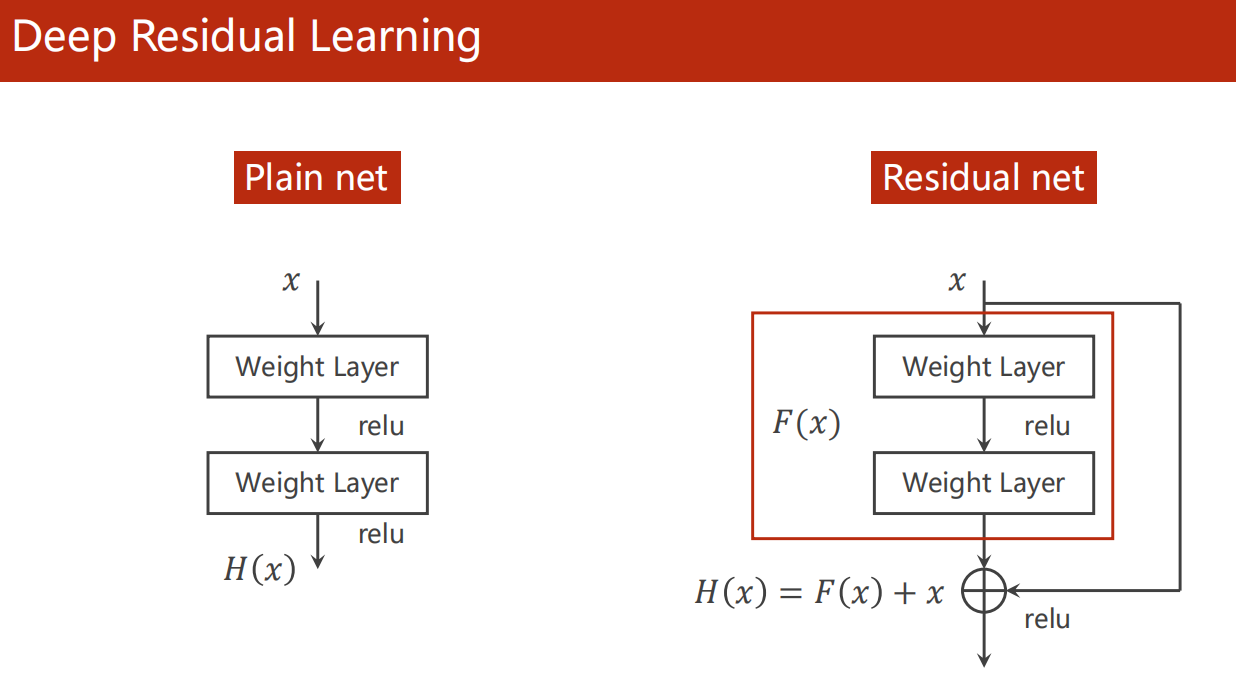
- 试看如下
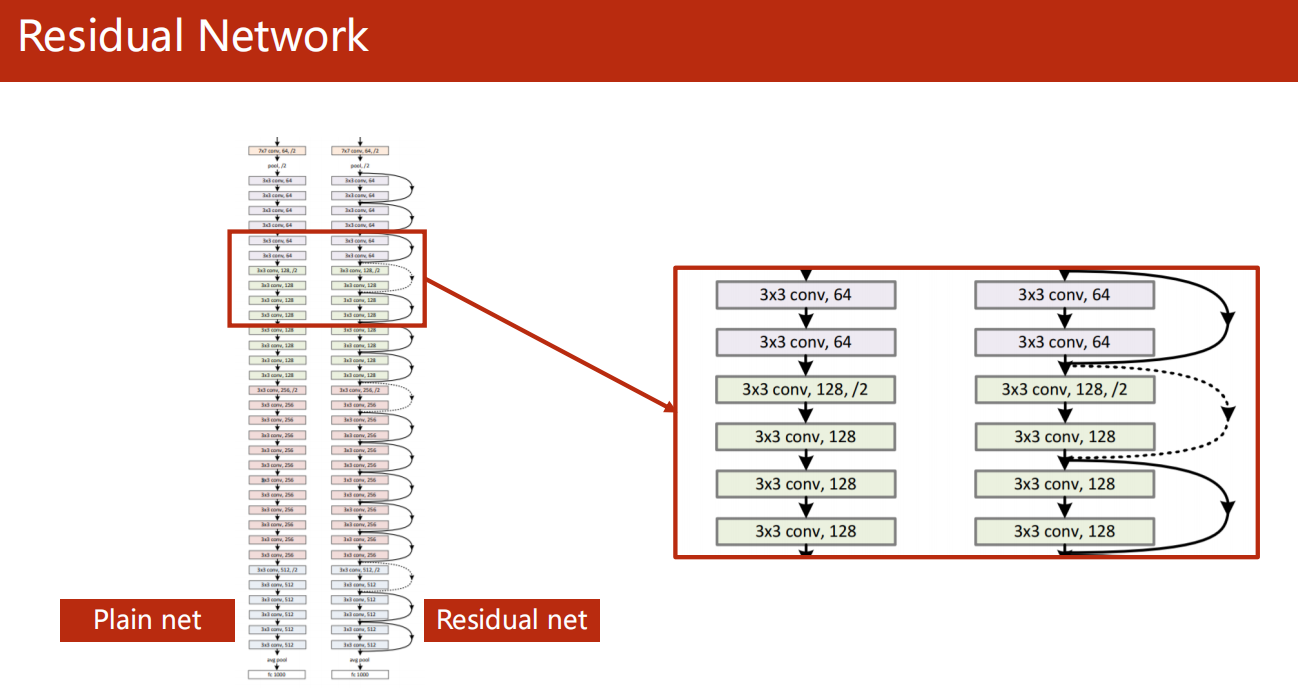
简单示例
-
架构

-
Residual 操作

-
代码流程

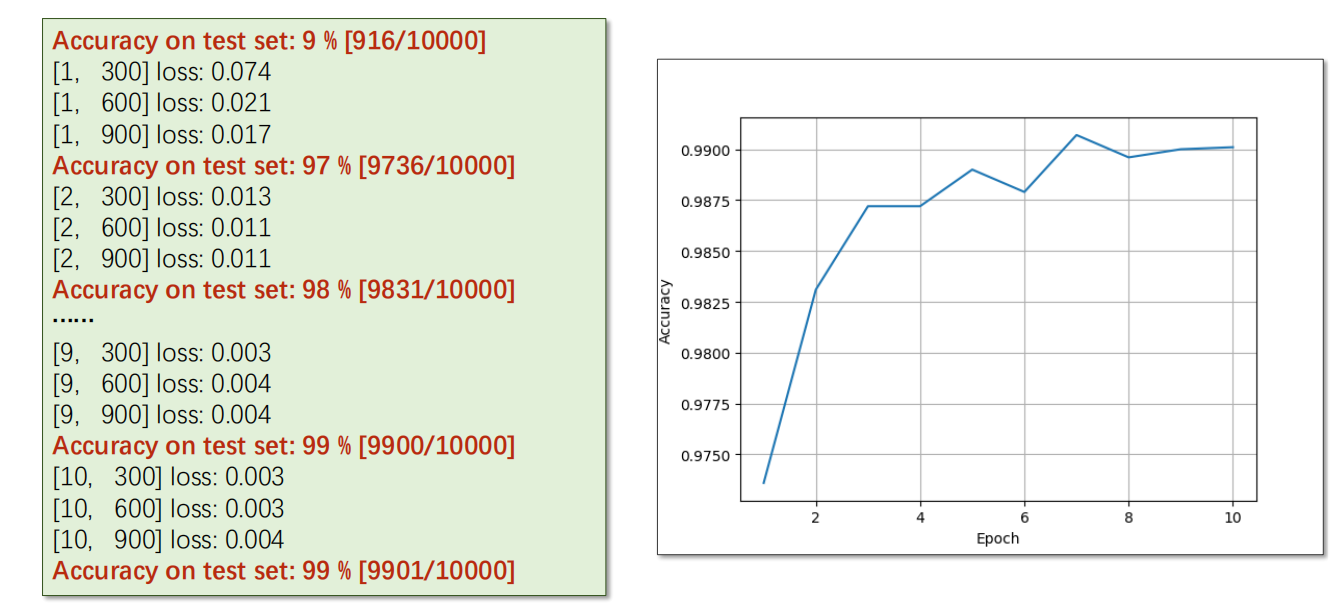
-
测试结果
*11.6 练习
-
Exercise 11-1: Reading Paper and Implementing
-
下面这篇论文中,有很多关于 Resiudal 操作的示例,尝试阅读执行。
1
He K, Zhang X, Ren S, et al. Identity Mappings in Deep Residual Networks[C]
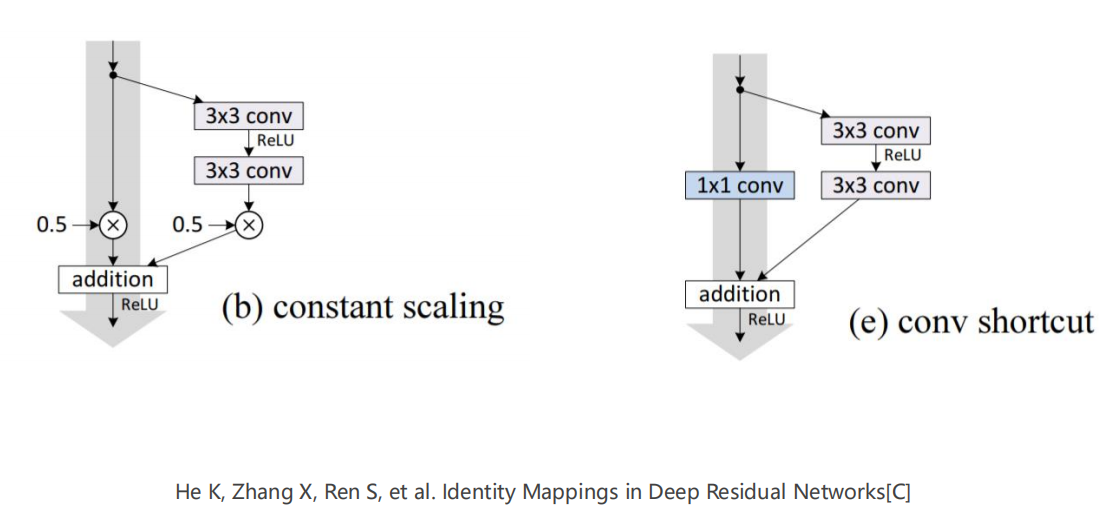
-
Exercise 11-2: Reading and Implementing DenseNet
-
阅读并执行下文的 DenseNet
1
Huang G, Liu Z, Laurens V D M, et al. Densely Connected Convolutional Networks[J]. 2016:2261-2269.
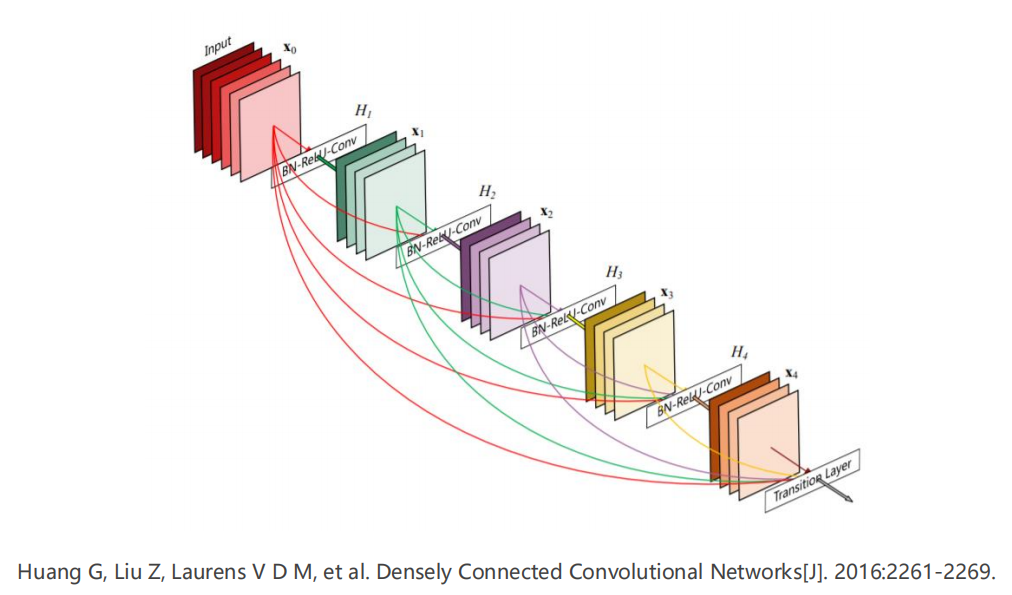
12、Basic RNN
- 特点:
- 序列 Data
- 循环共享权值
12.1 引入
-
什么是RNN?
Recurrent Neural Network 循环神经网络
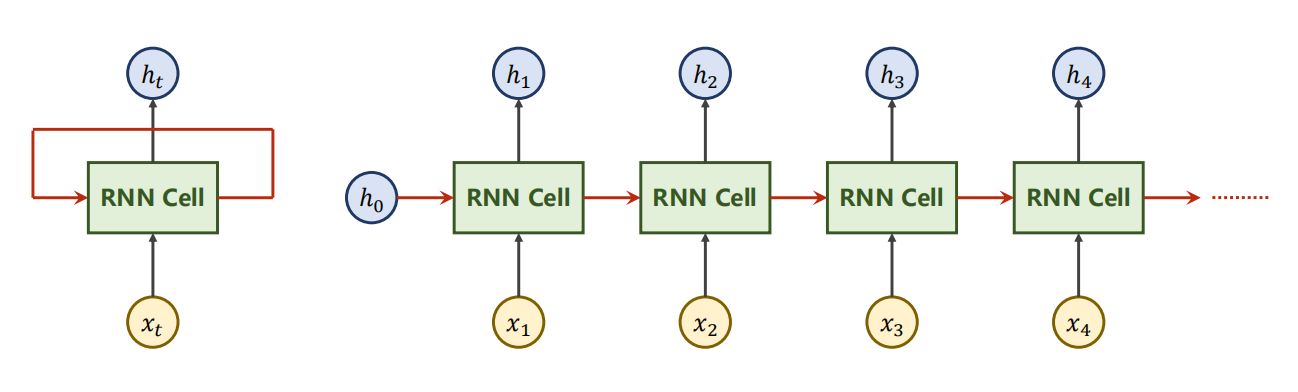
-
RNN单元 计算过程
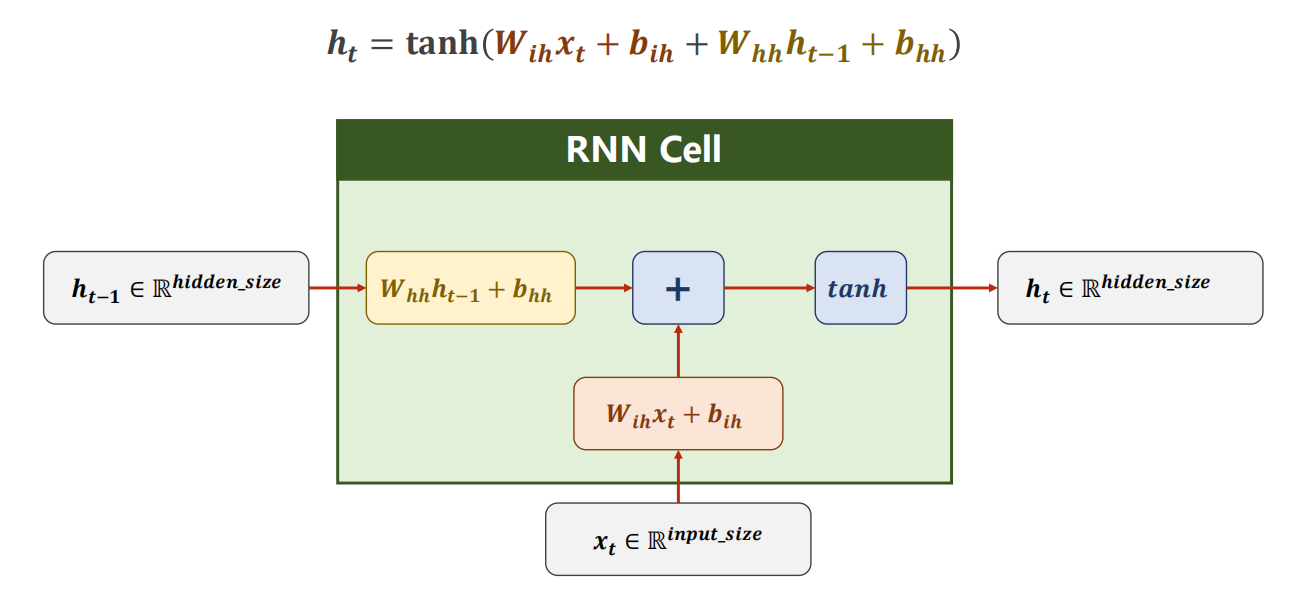
12.2 使用方法1:RNNCell
使用内容示意
RNNCell 是只一次的单元计算,需要你自己写循环,把 RNNCell 串起来。
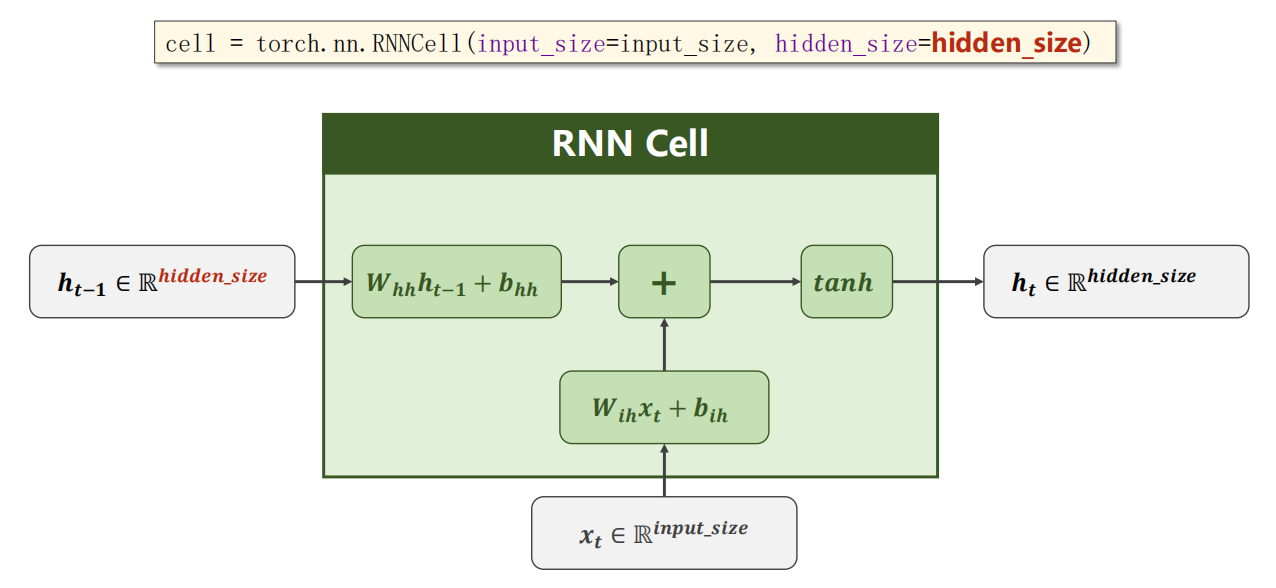
参数说明
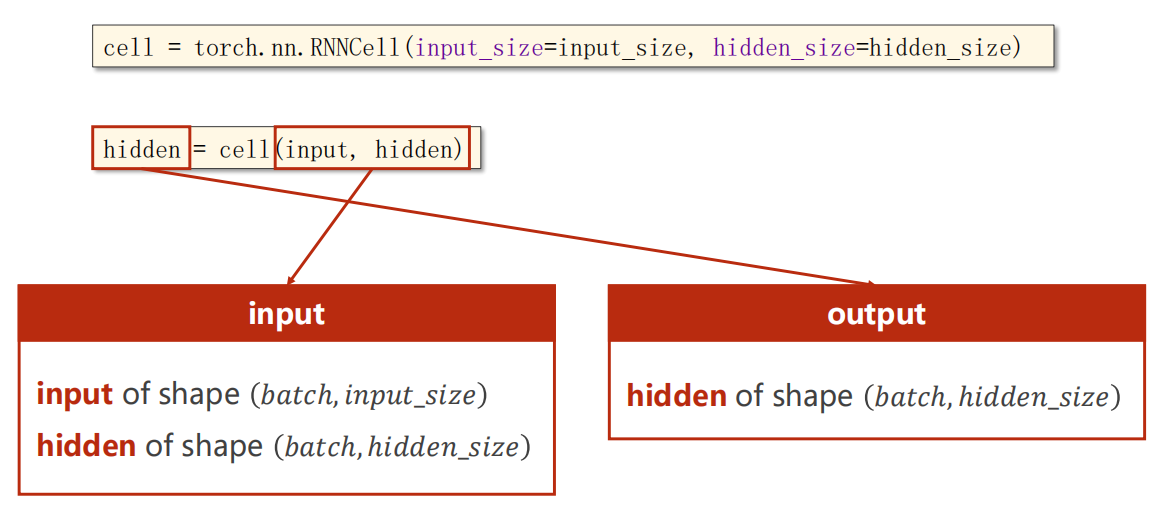

代码示例

12.3 使用方法2:RNN
使用内容示意
RNN 是直接把多个 RNNCell 循环都部署好了,不需要你手动写循环。
但也因此,你的input_size 和 hidden_size 维度是比前面Cell 的那种要高一个维度,用来指示多少个Cell 运算。
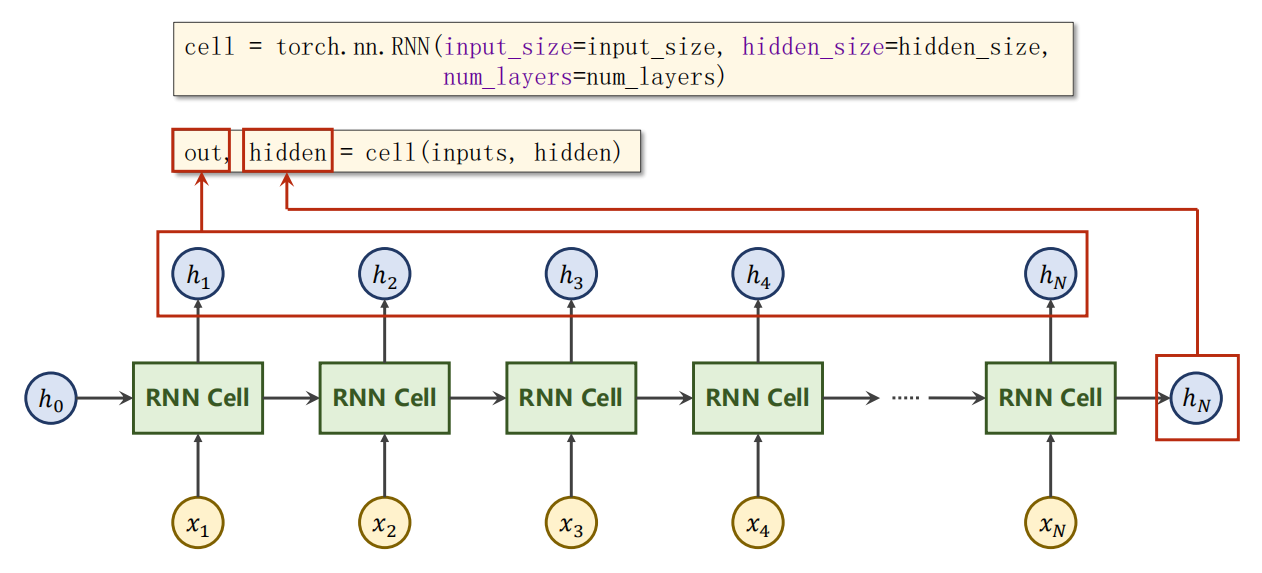
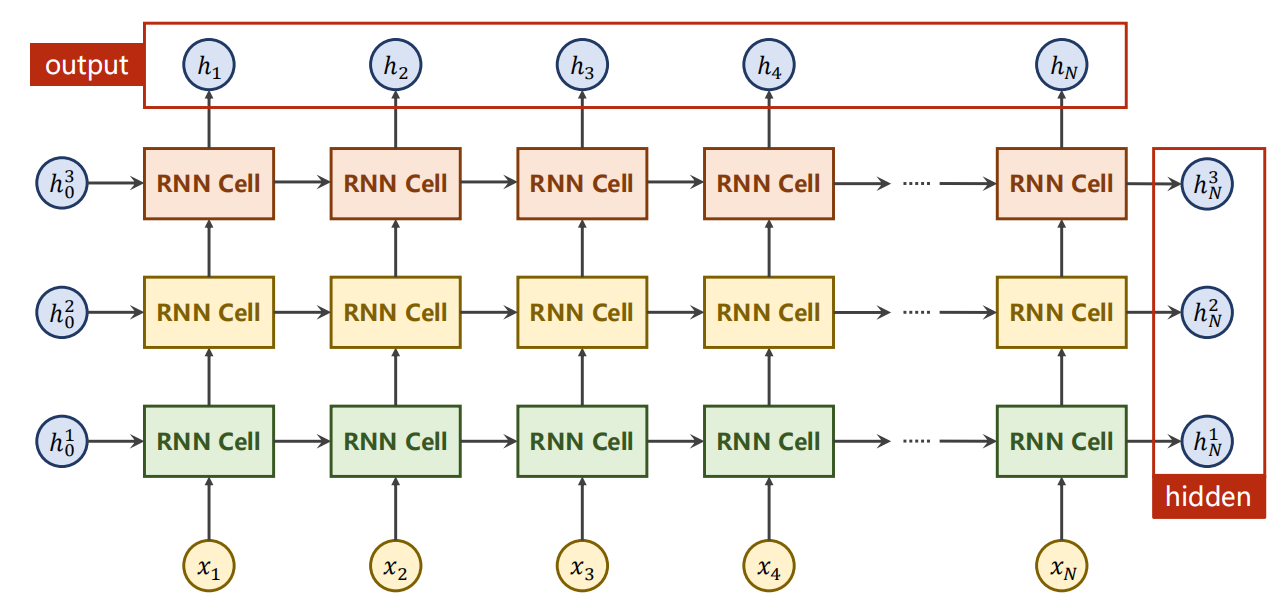
其中 num_layers 参数是指同一输入的处理层数,如下是多层的情况:
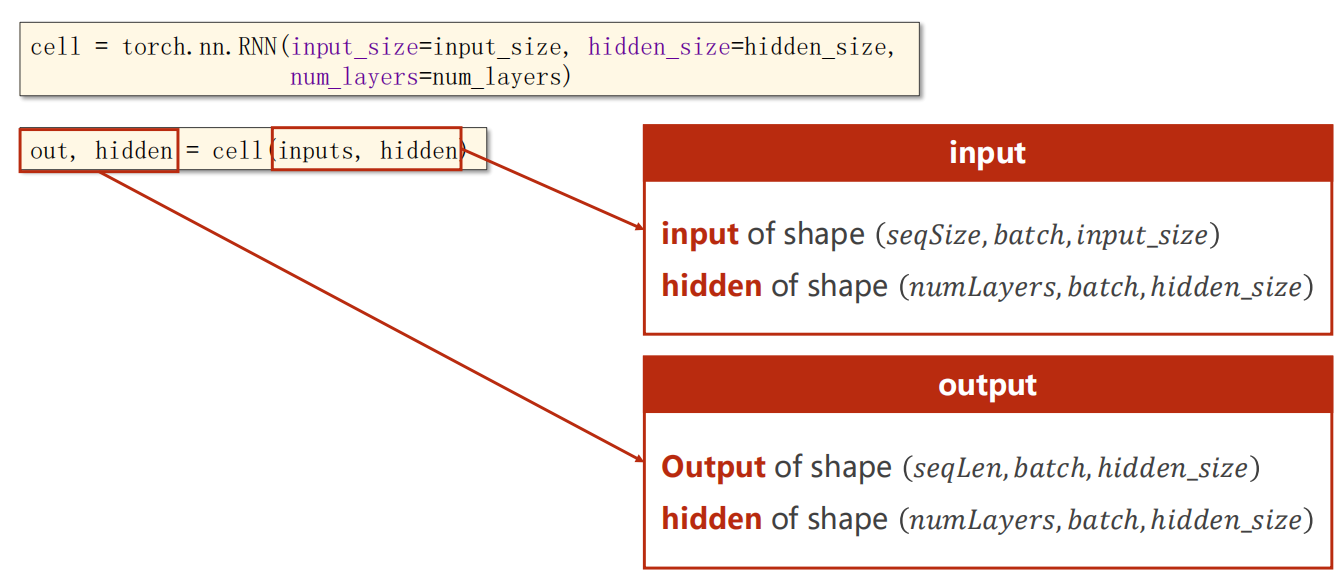
参数说明

这里还有一个参数,batch_first,表示是否把 batch_size 放在第一个维度(本来应该是第二个)


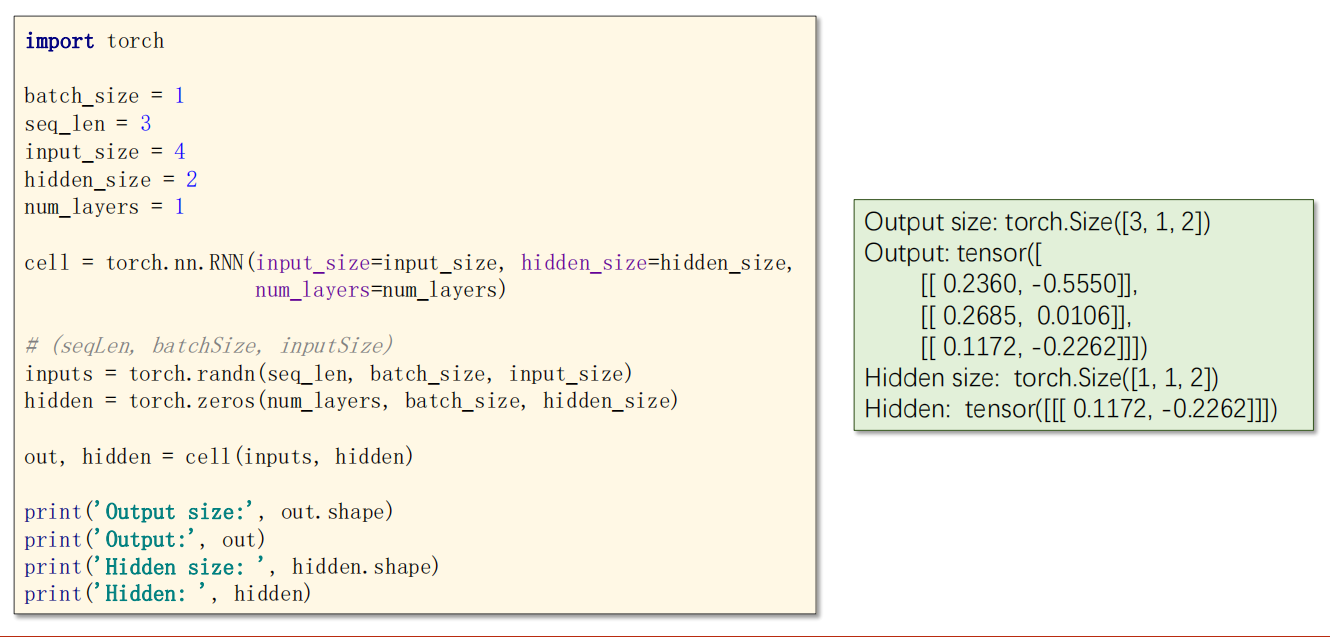
代码示例
12.4 示例:训练字符串输出
-
目标任务
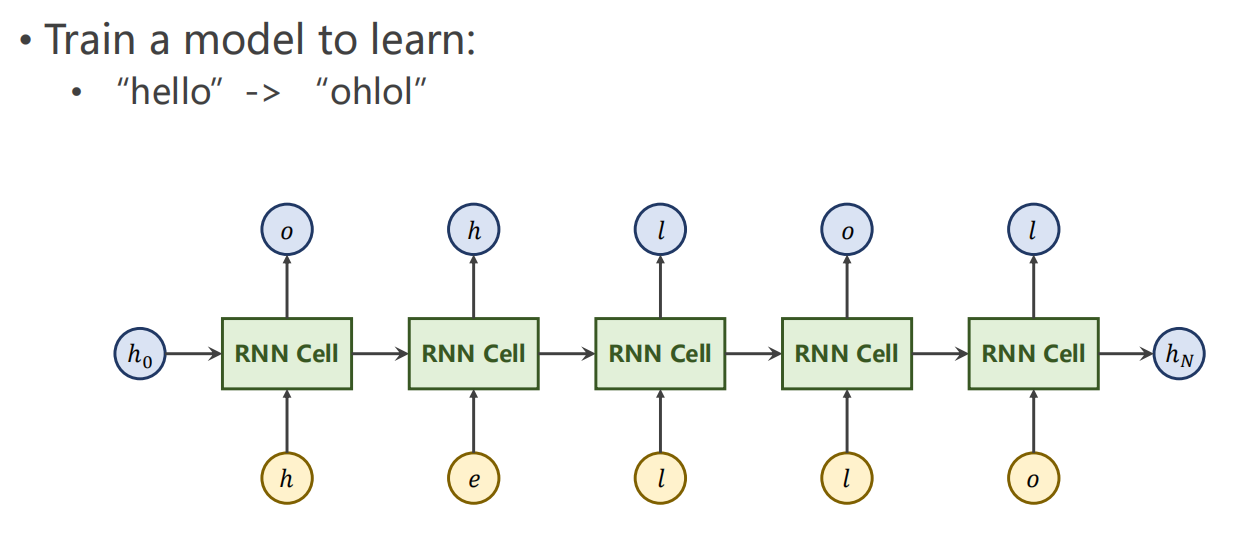
-
数据预处理
RNN 只能处理数字,因此我们建立字母到数字的索引字典。
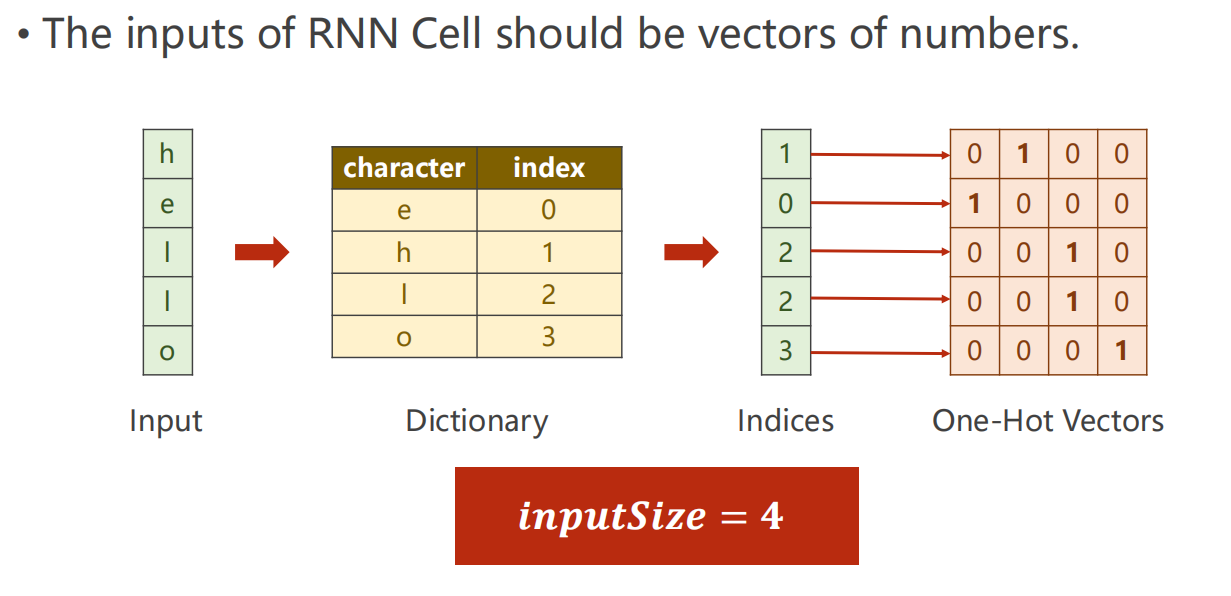
-
损失函数
采用 交叉熵 CrossEntropyLoss
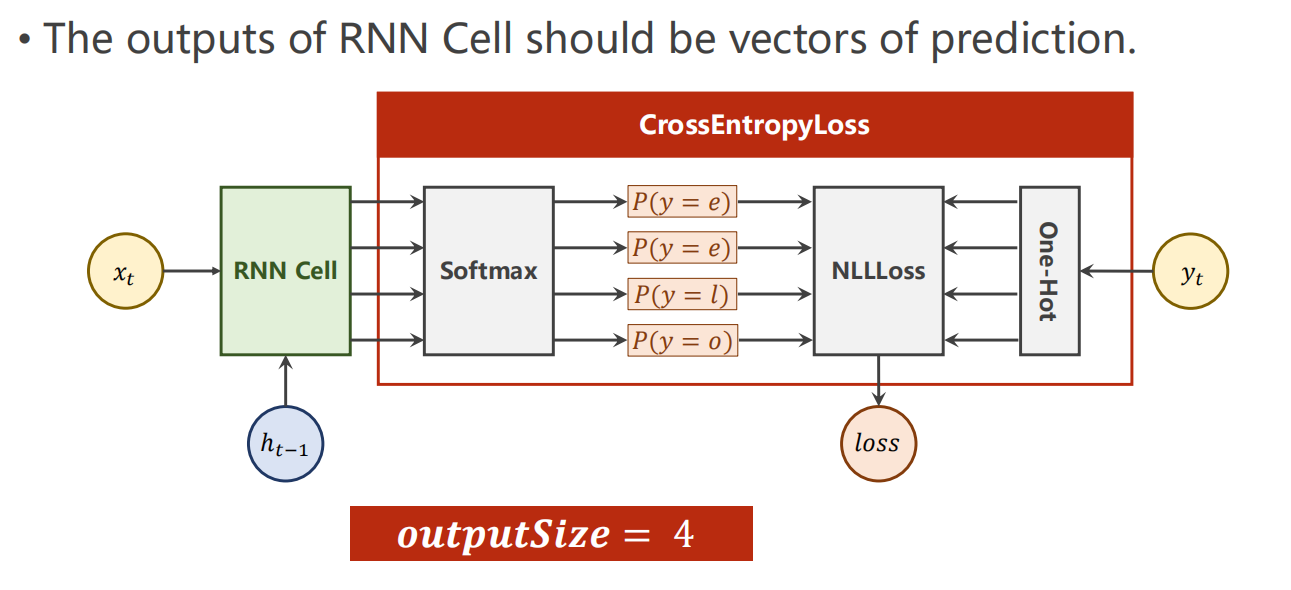
完整代码
1 | 暂无 |
12.5 Embedding 嵌入层
原理
-
关联字符与数字的方法
-
独热编码
特点: 高维度、稀疏、硬编码。
-
Embedding 嵌入层
特点:低维度、密集、学习自数据。
方法2更好。
-

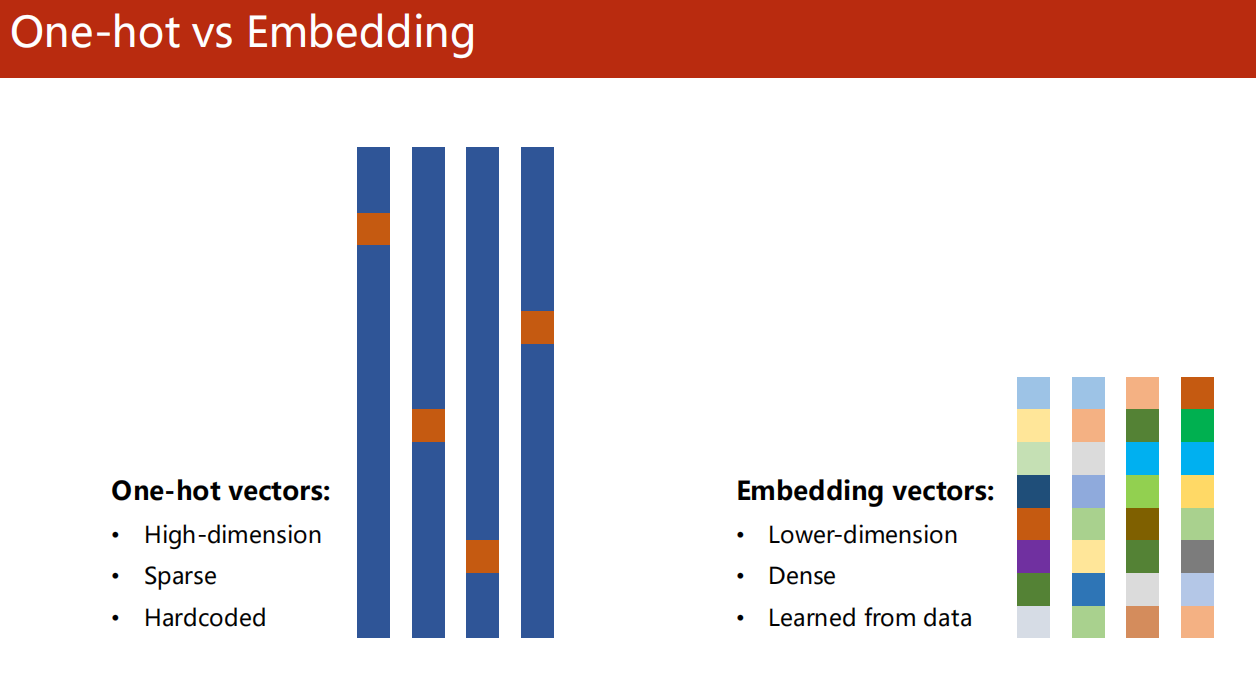
Embedding 层计算过程
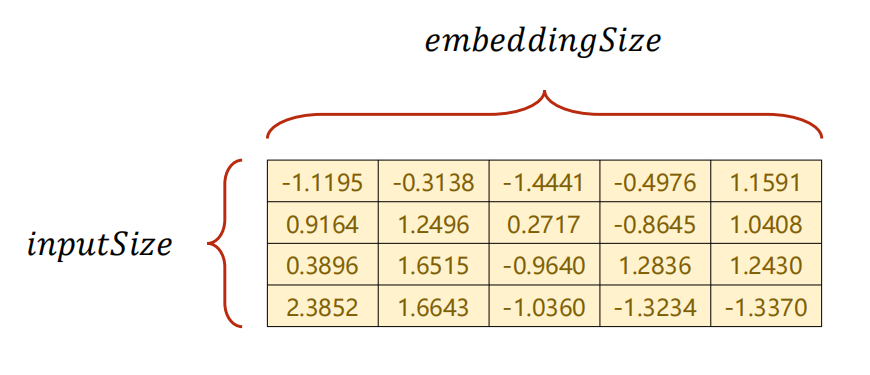
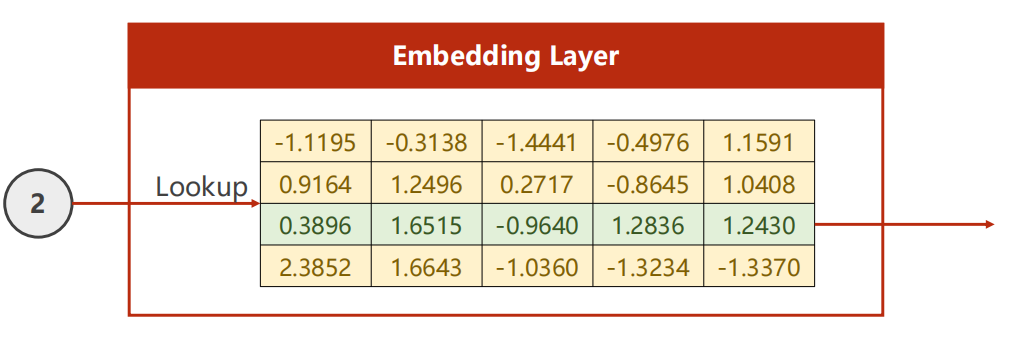
使用架构
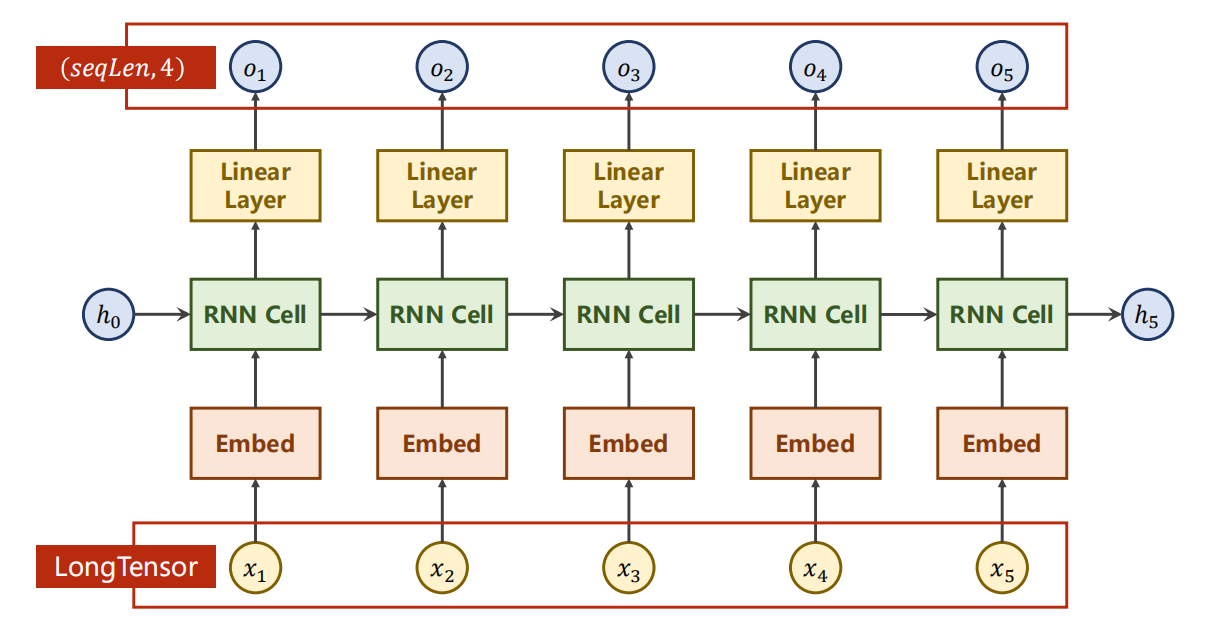
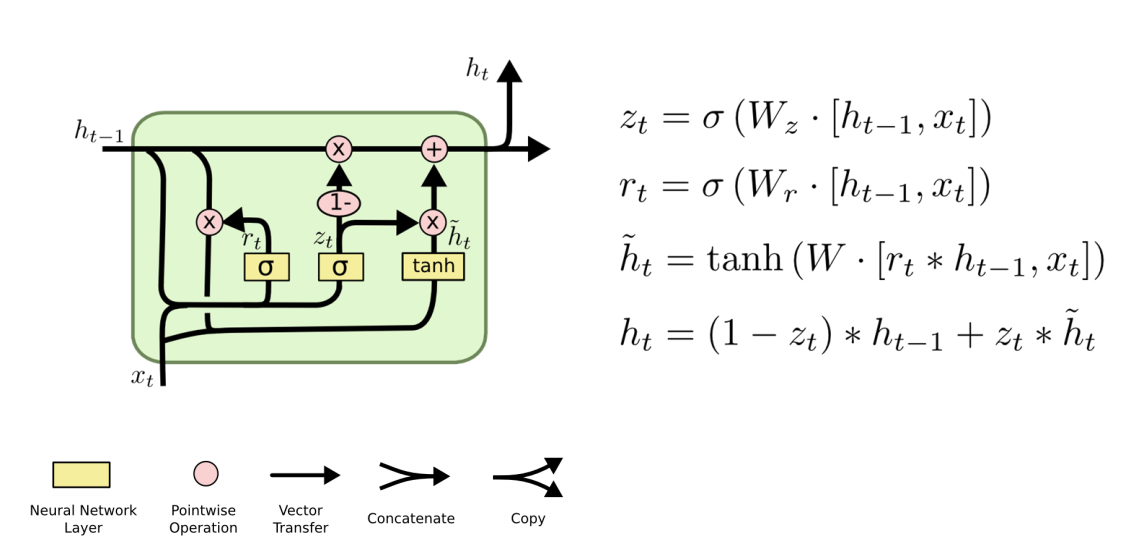
12.6 拓展:LSTM与GRU
-
LSTM
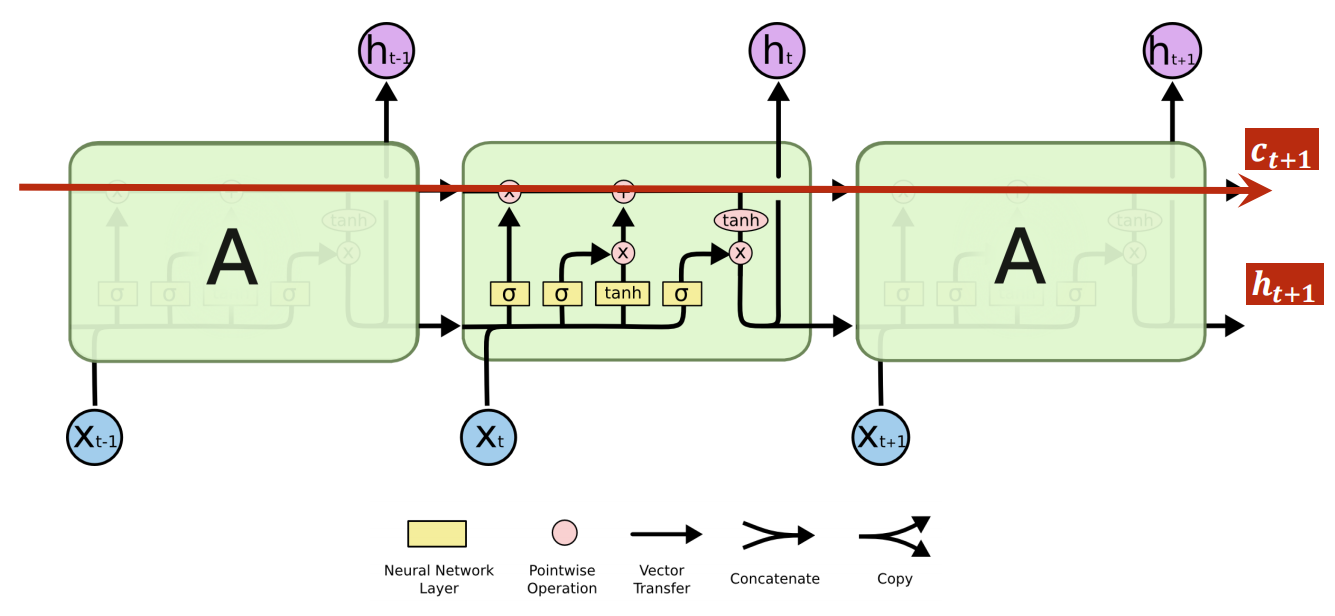

-
GRU

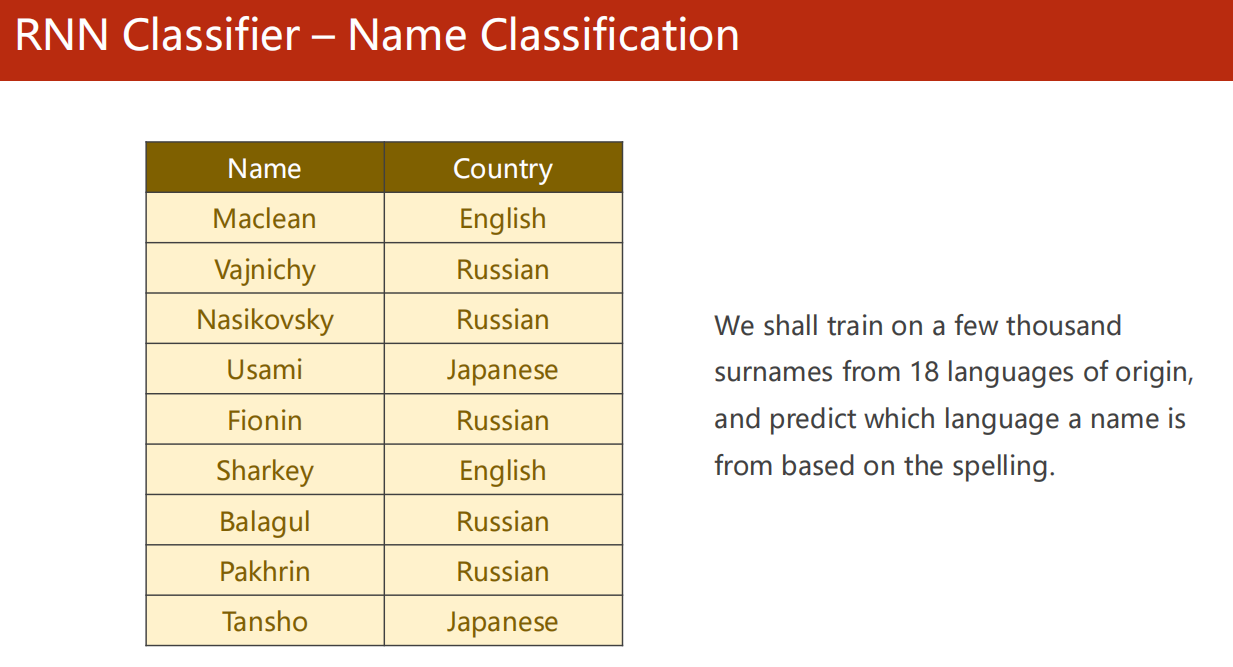
13、RNN Classifier
13.1 引入
-
姓名对应国家分类问题
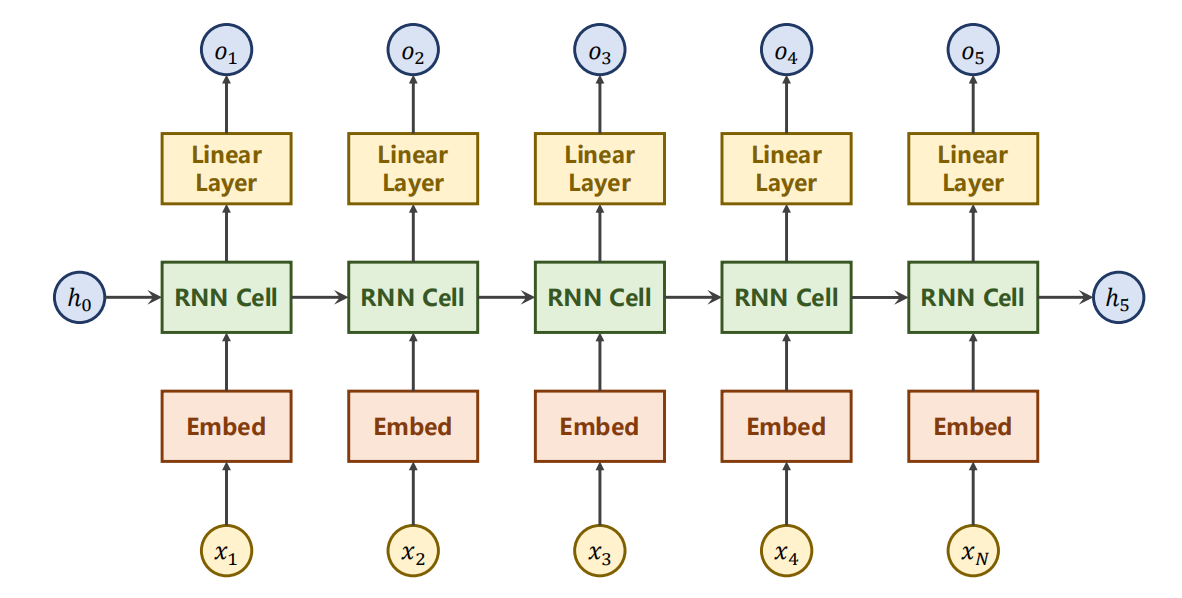
-
设计模型
-
本来可以仍然设计如下,
但是,我们实际上并不需要每次都输出 o(即便输出,我们也不知道是什么,也没有对应的 label ,没意义),
只有最后一次的输出 o 才是有效的。
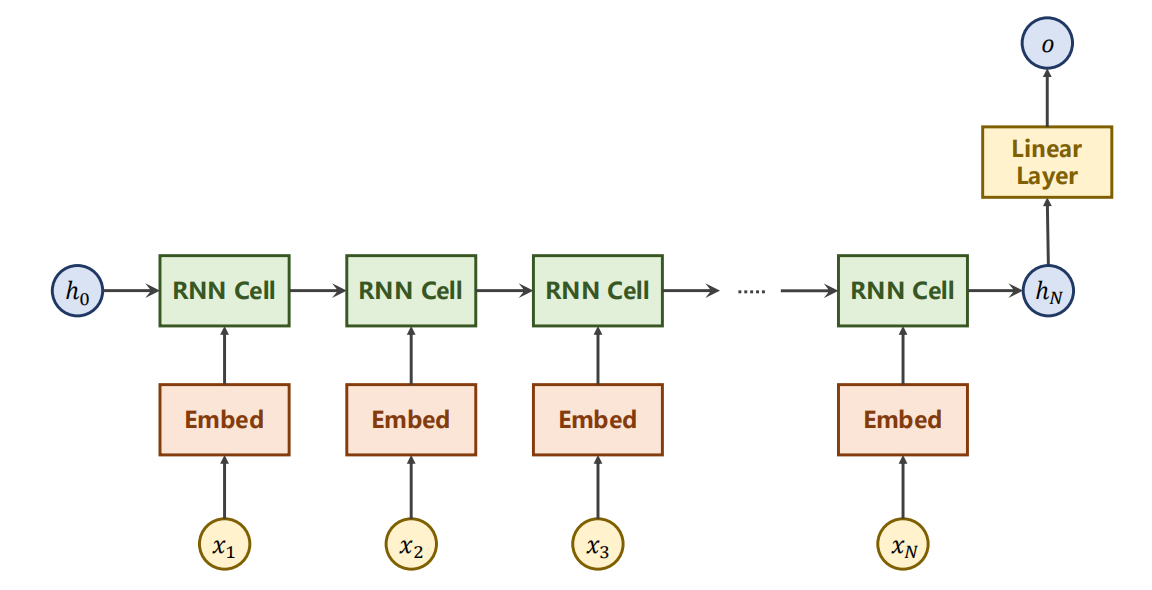
- 因此,我们可以去除,只留下最后一次的输出。
- 另外,我们改用 RGU 进行:
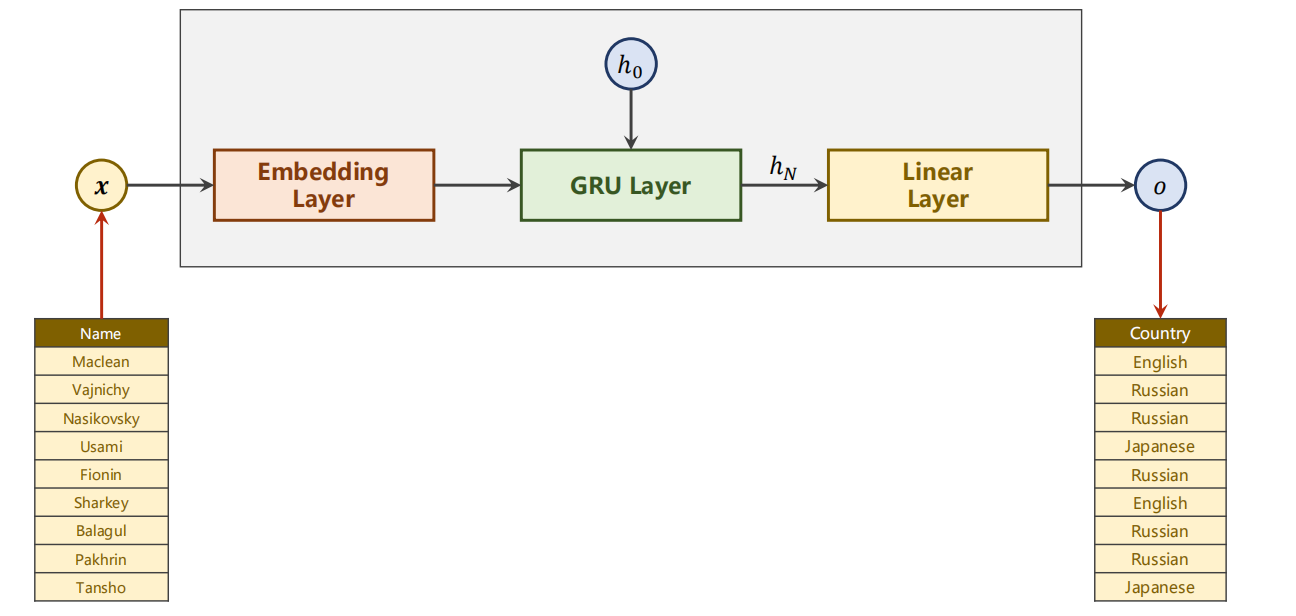
13.2 设计模型
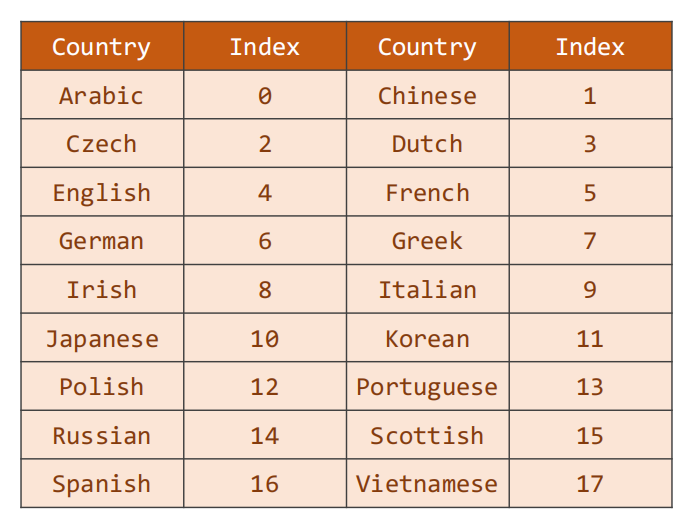
数据预处理
同理,无法处理字符串,我们需要先建立对应的数字索引,用来处理。

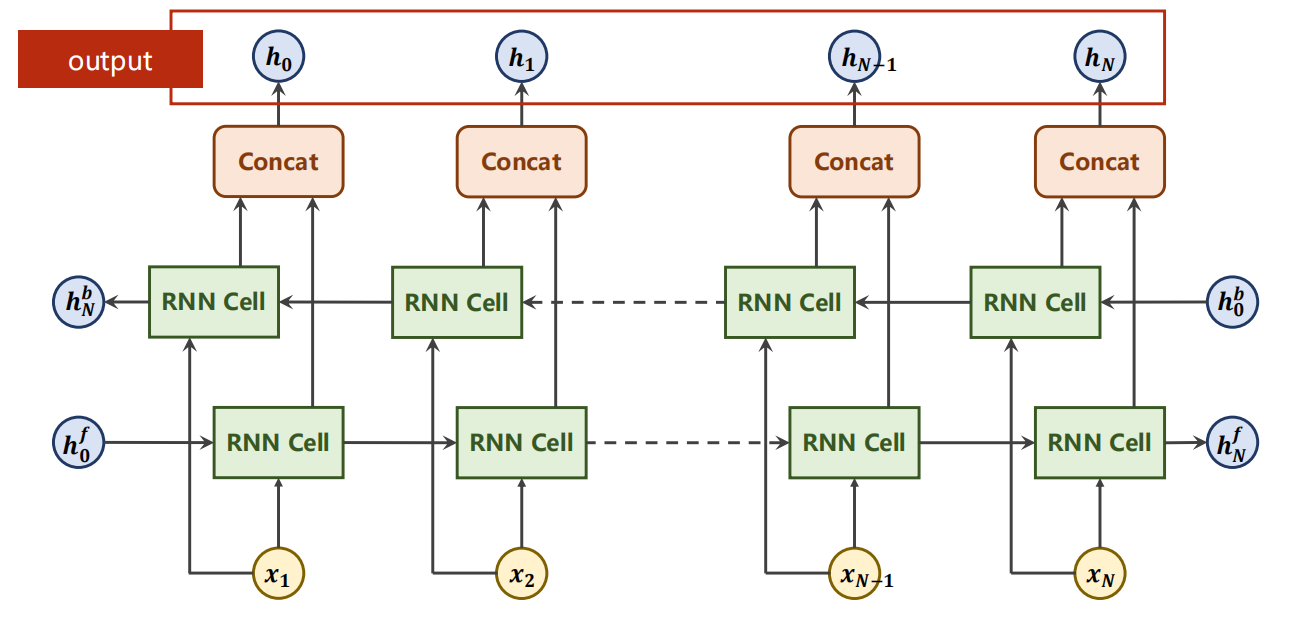
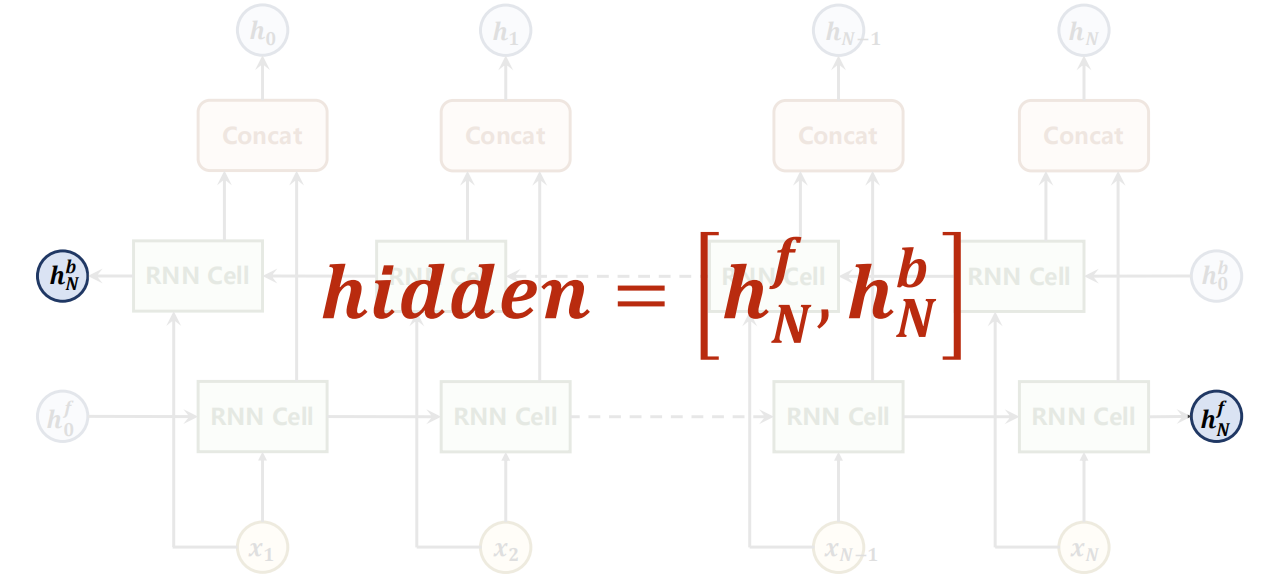
Bi-direction 参数
-
是否同时也进行反向的检测(不是反向传播)
若是,则输出output 会是每一次的左右两向的拼接的 h,
同时需要同时提供 左右两向的初始 h0f、b0b,
输出也会有 hNf 、 hNb两个。
完整代码
1 | 暂无 |
*13.3 练习题
-
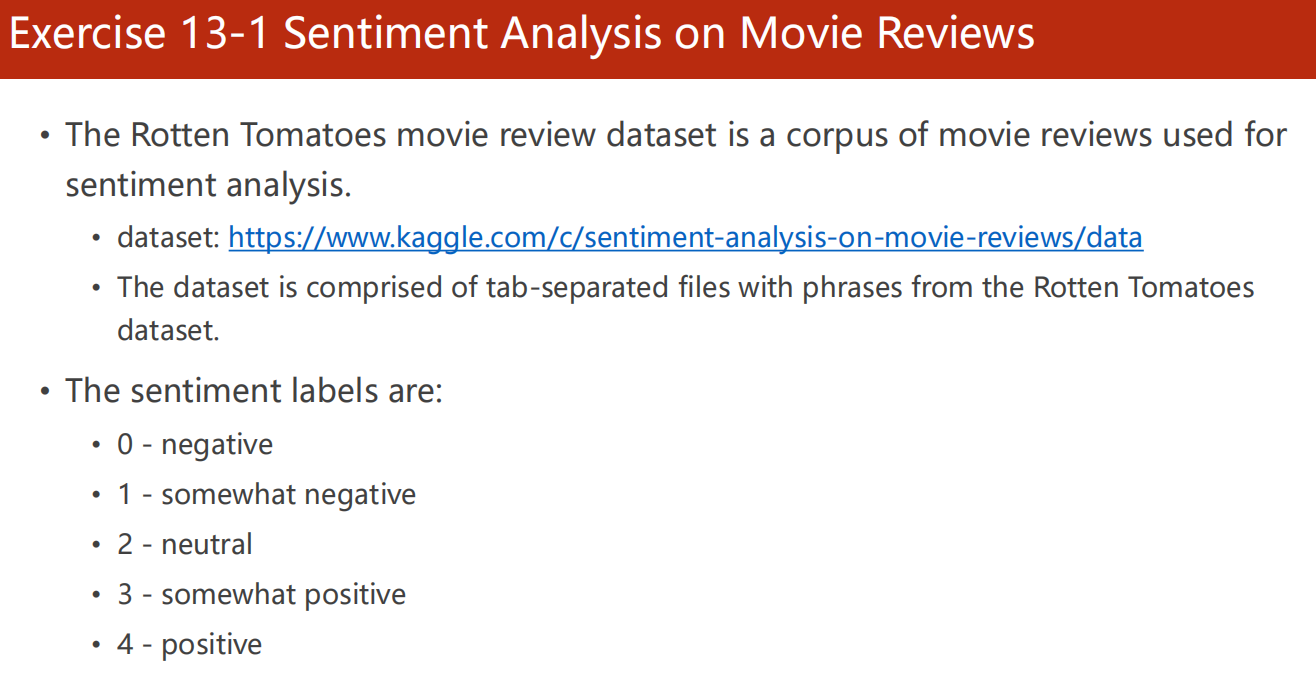
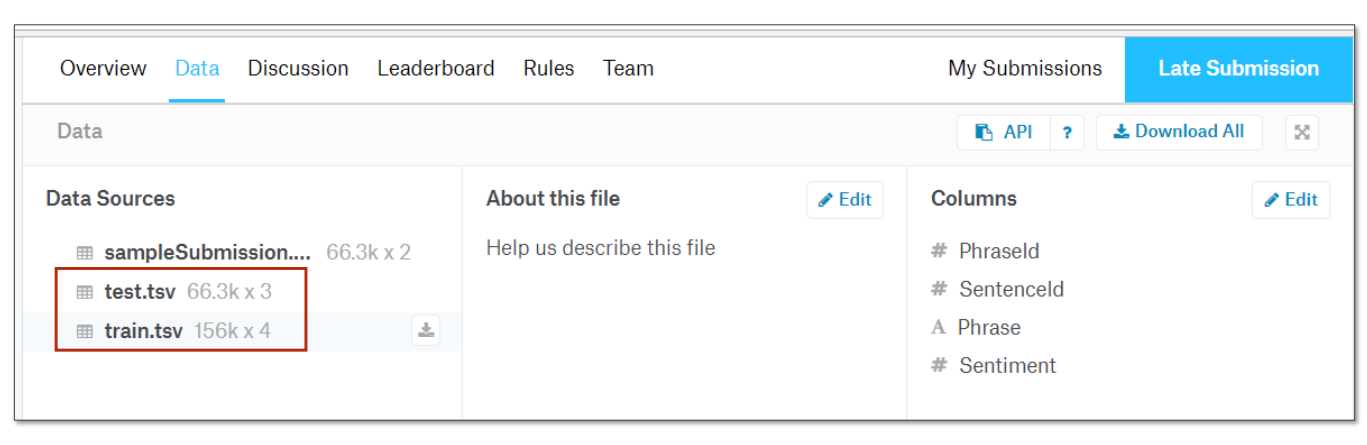
Exercise 13-1 Sentiment Analysis on Movie Reviews
-
分析《烂番茄》电影评论的情感程度。
数据集:Kaggle 数据集
该数据集由tab分隔的文件组成,其中包含来自烂番茄数据集的短语。
-
情感标签有:
- 0–消极
- 1–有点消极
- 2–中性
- 3–有点积极
- 4–积极