三、线性分类器

为什么从线性分类器开始？

  1. 形式简单、易于理解
  2. 通过层级结构（神经网络）或者高维映射（支撑向量机）可以形成功能强大的非线性模型

3.1 定义

  • 线性分类器

    是一种线性映射，将输入的图像特征映射为类别分数。

    C1-9

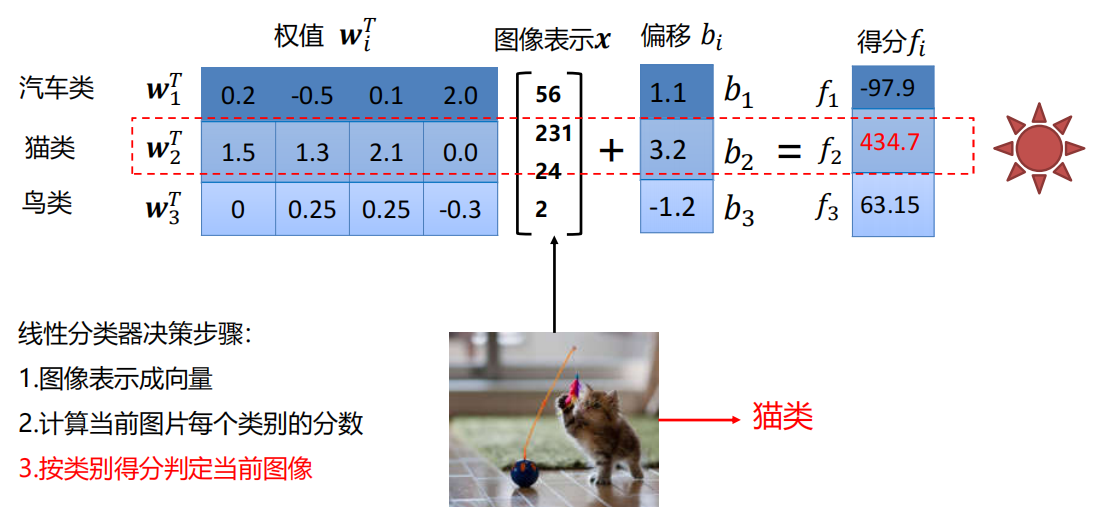
  • 示例

    C1-10

3.2 参数

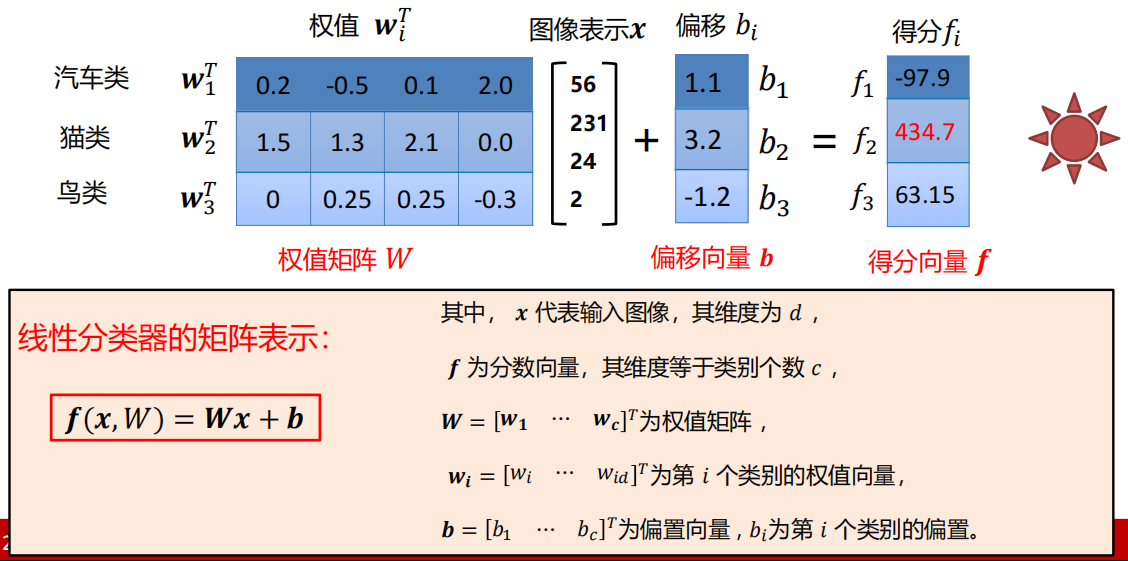
  • 矩阵表示

image-20240504182700821

  • 权值向量

C1-12

  • 决策边界

C1-13

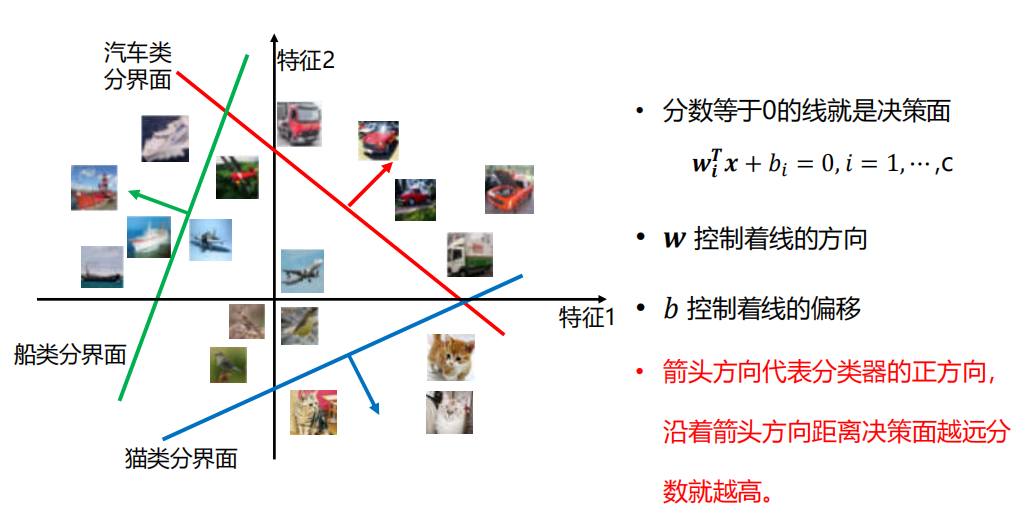
3.3 图像表示

将图像转换成向量的方法有很多，这里我们用一种最简单的方法，直接将图像矩阵转换成向量。

C1-8
C1-8-2

3.4 损失函数

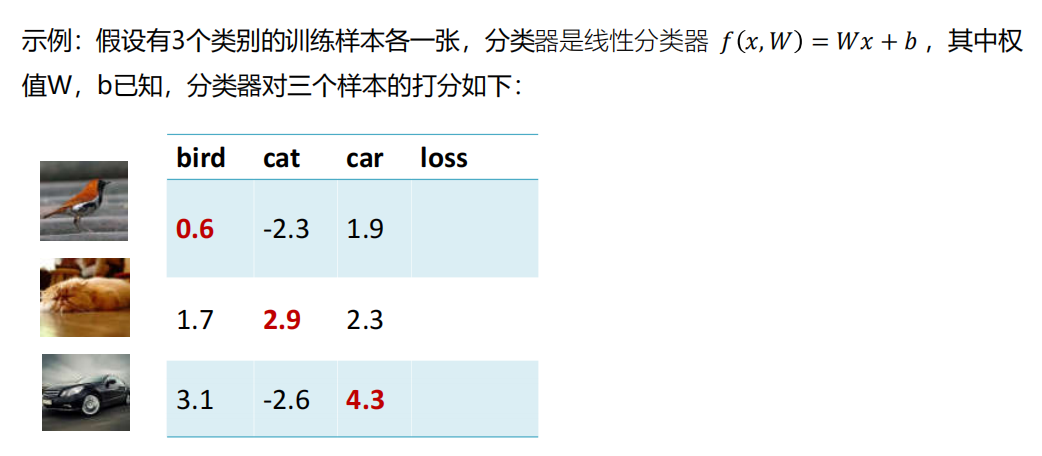
对示例样本，分类器1与分类器2的分类谁的效果更好？

需要损失函数来帮忙！

  • 损失函数搭建了模型性能与模型参数之间的桥梁，指导模型参数优化。

    • 损失函数是一个函数，用于度量给定分类器的预测值与真实值的不一致程度，其输出通常是一个非负实值。
    • 其输出的非负实值可以作为反馈信号来对分类器参数进行调整，以降低当前示例对应的损失值，提升分类器的分类效果。

  • 一般定义

    C1-14

多类支撑向量机损失

C1-15
  • 示例
    C1-16

疑问

C1-17

  • 多类支撑向量机损失 L 的最大/最小值会是多少？

    最大：无穷大

    最小：0

  • 如果初始化时w和b很小，损失 L 会是多少？

    类别数目减一。（可用于检测损失函数是否写对了）

  • 在总损失计算时，如果用求和代替平均?

    可以，但是若是每个分组的大小不同，就不可以。

  • 若使用平方损失，最后模型会一样吗？

    不一样。

3.5 正则项

假设存在一个W使损失函数L=0，这个W是唯一的吗？

不唯一！

C1-18

不唯一的W ，那么选择哪个更好呢？

加入正则项，使得结果一定唯一！

  • 正则损失与超参数

    C1-19

  • 正则项让模型有了偏好！

  • 常用

    • L1正则项

      R(W)=∑k∑j∣wk,j∣R(W) = \sum \limits_{k} \sum \limits_{j} |w_{k,j}|

    • L2正则项

      R(W)=∑k∑jwk,j2R(W) = \sum \limits_{k} \sum \limits_{j} w_{k,j}^{2}

      L2正则损失对大数值权值进行惩罚，喜欢分散权值，鼓励分类器将所有维度的特征都用起来，而不是强烈的依赖其中少数几维特征。

    • Elastic net(L1+L2)

      R(W)=∑k∑jβwk,j2+∣wk,j∣R(W) = \sum \limits_{k} \sum \limits_{j} \beta w_{k,j}^{2} + |w_{k,j}|

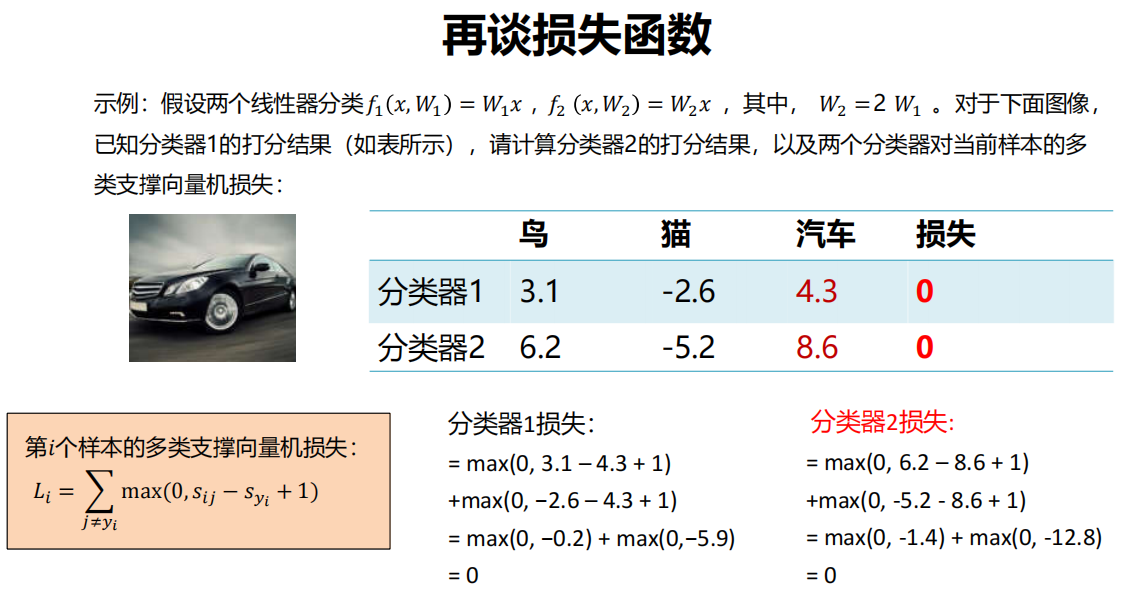
示例：

  • 样本：x=[1,1,1,1]x=[1,1,1,1]

  • 分类器

    • 分类器1：w1=[1,0,0,0]w_1 = [1,0,0,0]
    • 分类器2：w2=[0.25,0.25,0.25,0.25]w_2 = [0.25,0.25,0.25,0.25]

  • 输出

    w1Tx=w2Tx=1w_1^T x = w_2^T x =1

  • L2正则损失

    R(w1)=1R(w_1) = 1

    R(w2)=0.25R(w_2) = 0.25

分类器2总损失小

3.6 参数优化

  • 参数优化是机器学习的核心步骤之一。

  • 它利用损失函数的输出值作为反馈信号来调整分类器参数，以提升分类器对训练样本的预测性能。

  • 目标

    损失函数 L 是一个与参数 w 有关的函数，

    优化的目标就是找到使损失函数 L 达到最优的那组参数 w 。

  • 方法

    1. 直接对 w 求偏导，∂L∂w=0\frac{\partial L}{\partial w} = 0​ 的点的 w 就是最优参数。

      通常，L 形式比较复杂，很难从这个等式直接求解出 W！

      因此，需要后面的方法。

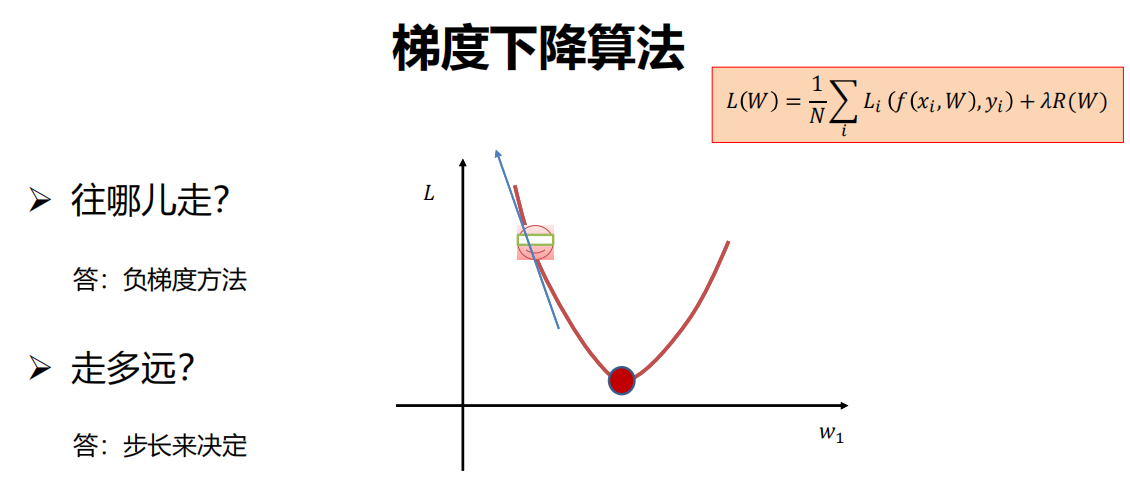
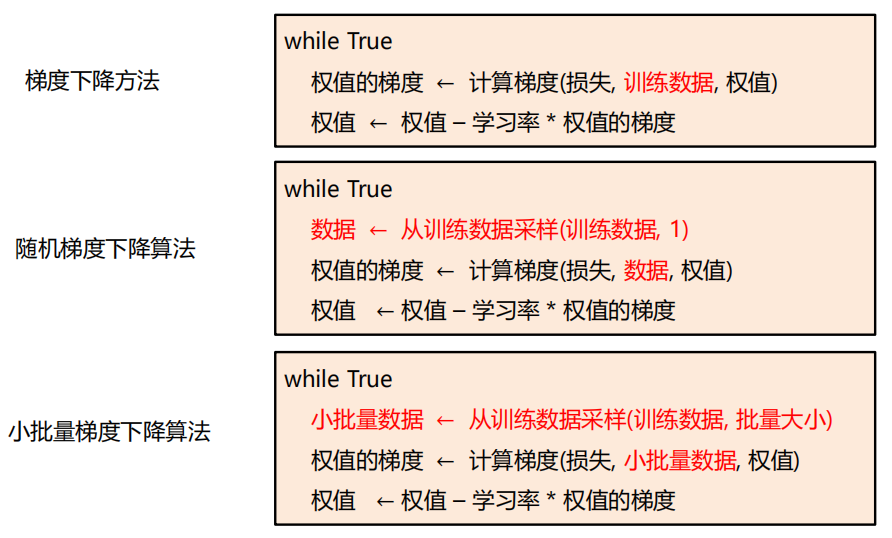
    2. 梯度下降

    3. 随机梯度下降

    4. 小批量梯度下降

    C1-27

(1) 梯度下降

C1-20

  • 一种简单而高效的迭代优化方法！

  • 利用所有样本计算损失并更新梯度。

C1-21

  • 计算梯度的方法

    1. 数值梯度: 近似, 慢, 易写
    2. 解析梯度: 精确, 快, 易错

    既然如此，数值梯度有什么作用？

    答：求梯度时一般使用解析梯度，而数值梯度主要用于解析梯度的正确性校验（梯度检查）。

    C1-22 C1-23

  • 计算效率

    由于利用所有样本计算损失并更新梯度，

    当N很大时，权值的梯度计算量很大！

    由此引出后面的 随机梯度下降 和 小批量随机梯度下降。

    C1-24

(2) 随机梯度下降

C1-25

(3) 小批量梯度下降

image-20240504193058460

3.7 数据集划分

C1-28
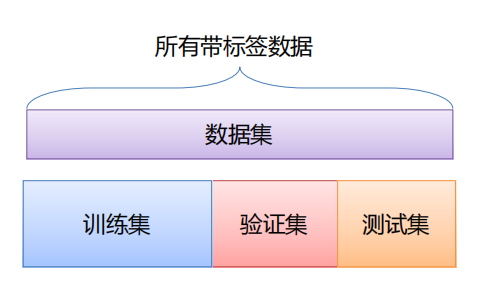
  1. 训练集用于给定的超参数时分类器参数的学习
  2. 验证集用于选择超参数
  3. 测试集评估泛化能力

问题：

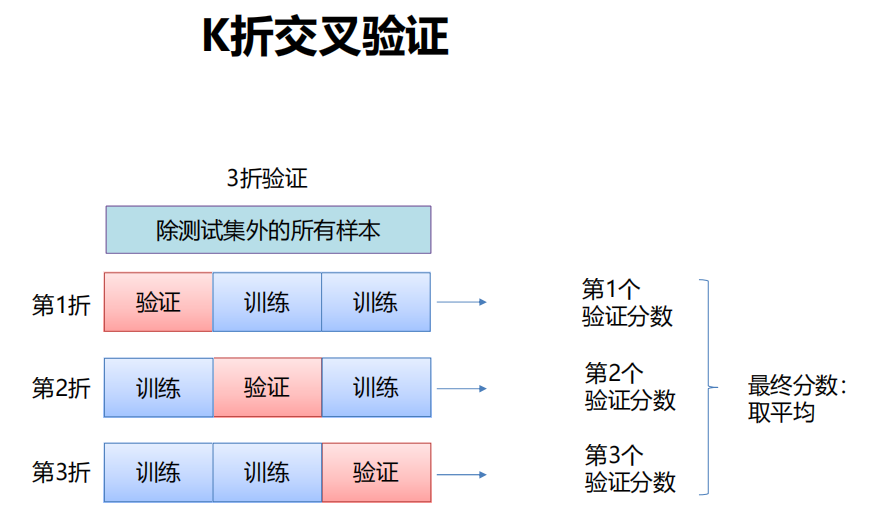
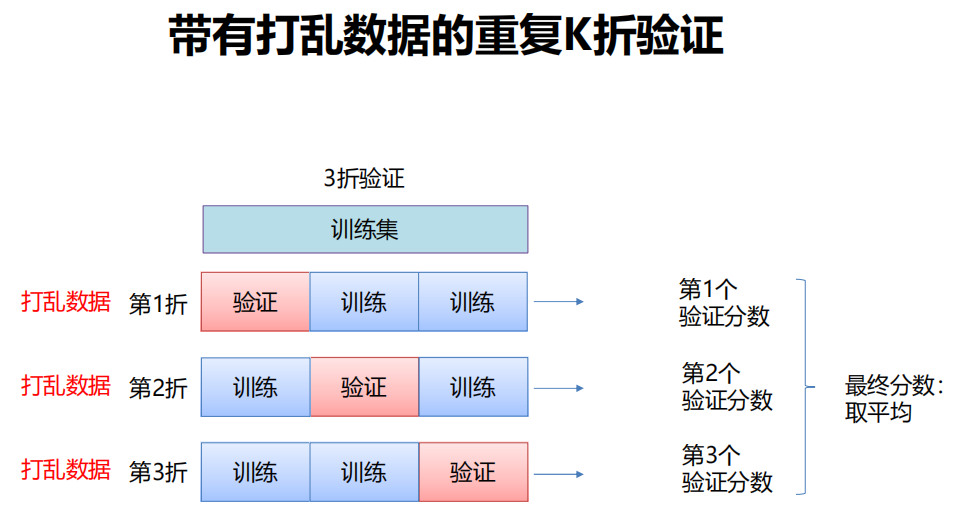
如果数据很少，那么可能验证集包含的样本就太少，从而无法在统计上代表数据。

发现：

如果在划分数据前进行不同的随机打乱，最终得到的模型性能差别很大，那么就存在这个问题。

接下来会介绍 K 折验证与重复的K 折验证，它们是解决这一问题的两种方法。

  • K折交叉验证

    C1-29

  • 带有打乱数据的重复K折验证

    C1-30

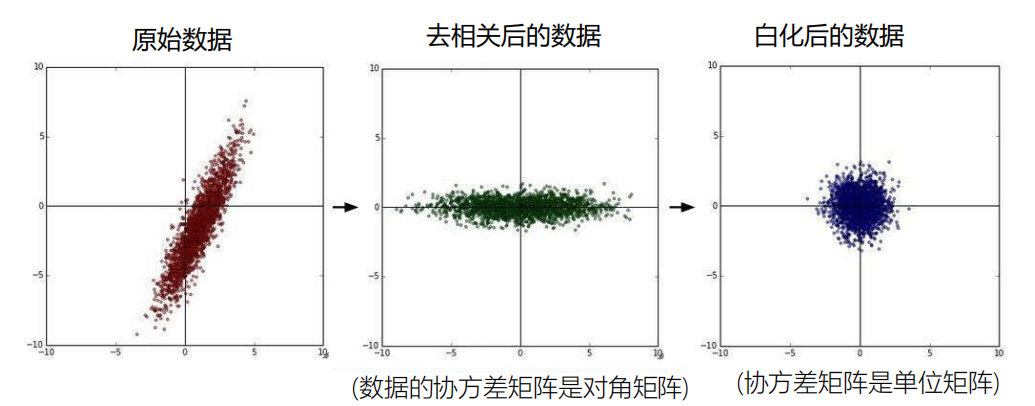
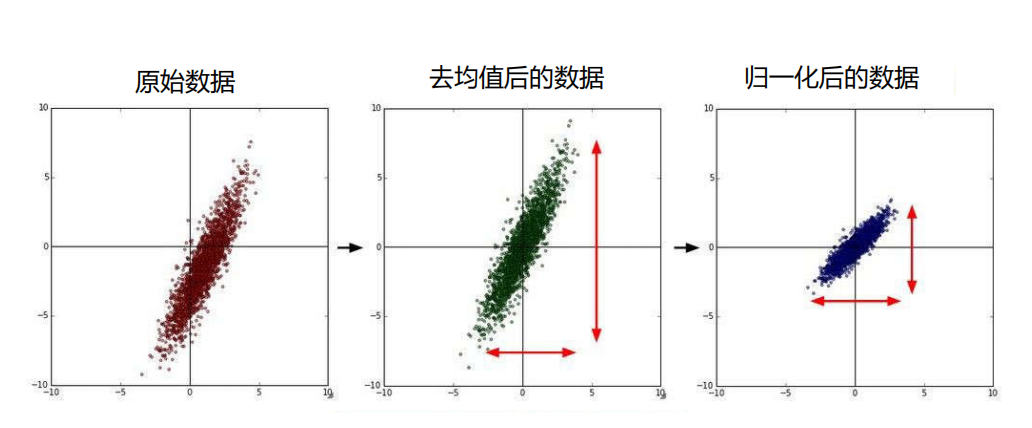
3.8 数据预处理

  • 处理方法1

    C1-31

  • 处理方法2

    C1-32