CVDL - 全连接神经网络
四、全连接神经网络
4.0 整体架构
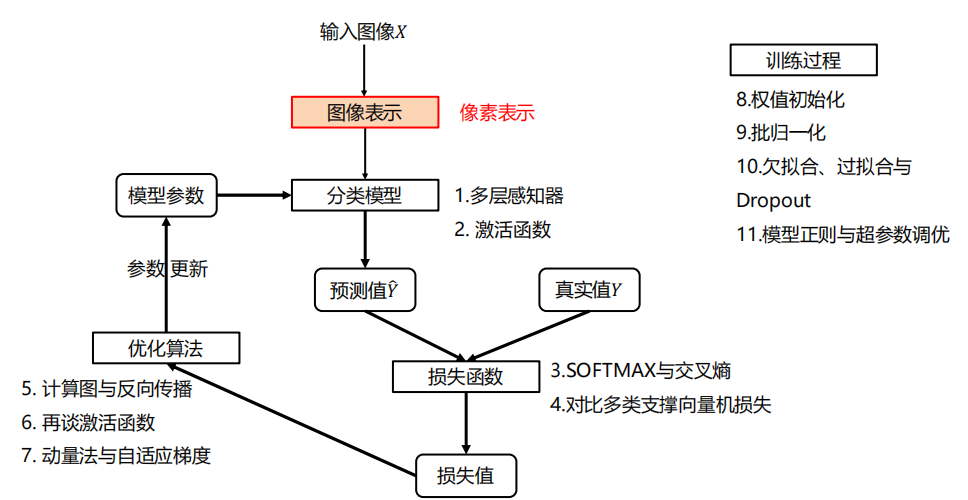
图像表示
与前面一样,直接利用原始像素作为特征,展开为列向量。

4.1 多层感知器
回顾前面,线性分类器是:

-
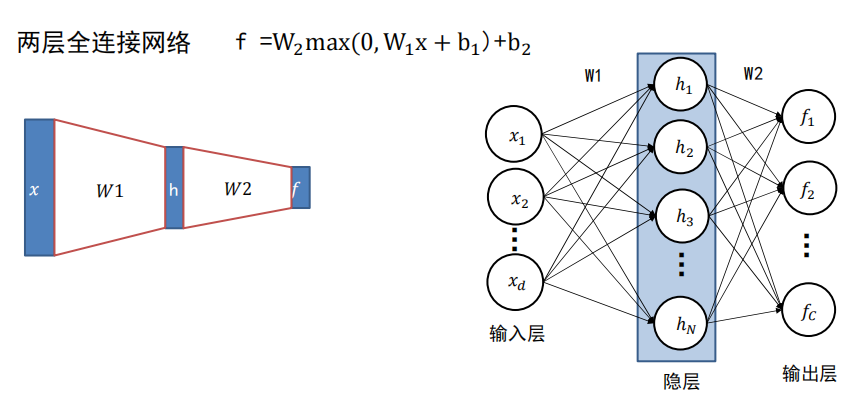
全连接神经网络:
全连接神经网络级联多个变换来实现输入到输出的映射。
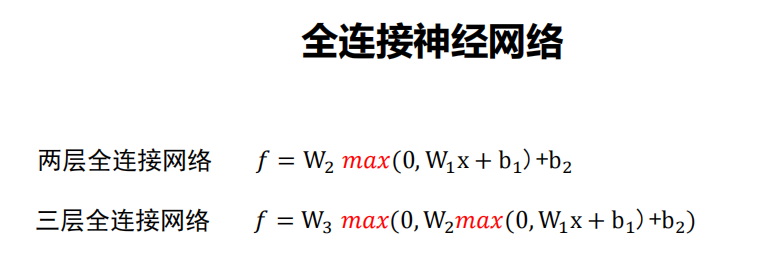
注:非线性操作是不可以去掉!
-
理解权值
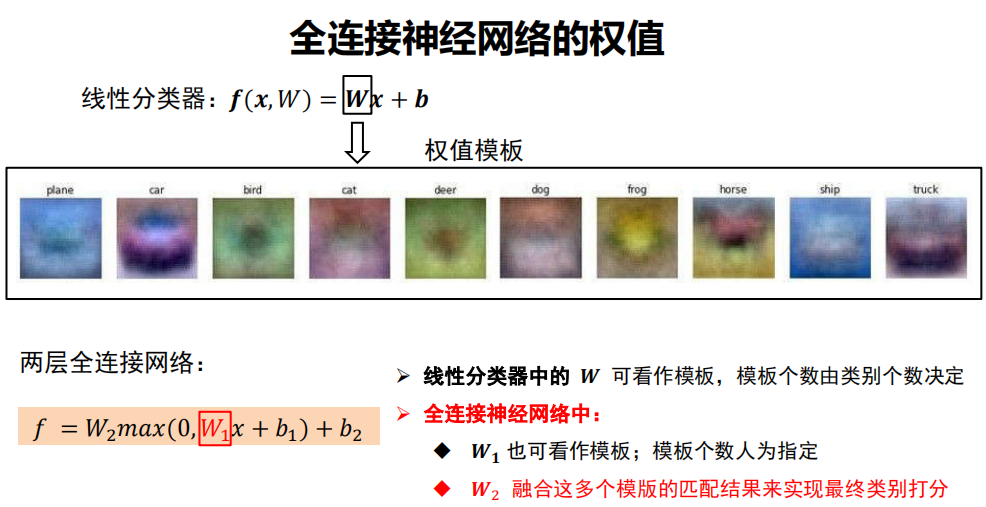
全联接神经网络的描述能力更强。
因为调整 行数 等于 增加模板个数,分类器有机会学到两个不同方向的马的模板。
-
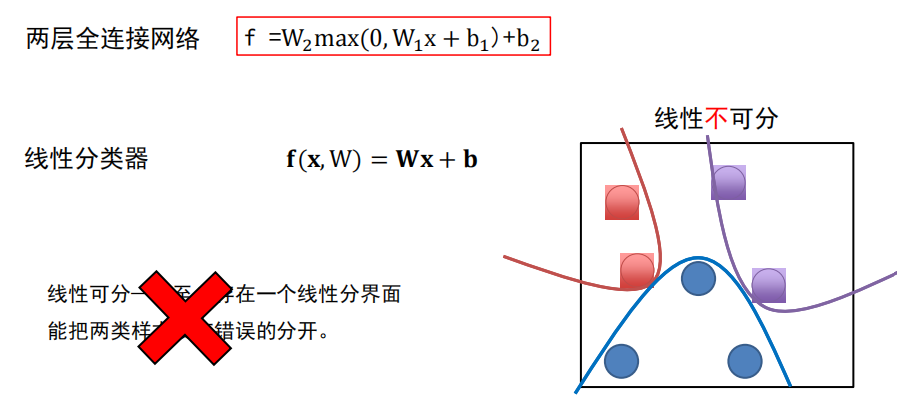
线性可分:线性分类器

-
线性不可分:全连接神经网络
绘制
命名
4.2 激活函数
激活函数是全连接神经网络中的一个重要部分,缺少了激活函数,全连接神经网络将退化为线性分类器。
-
必要性

-
常用的激活函数

-
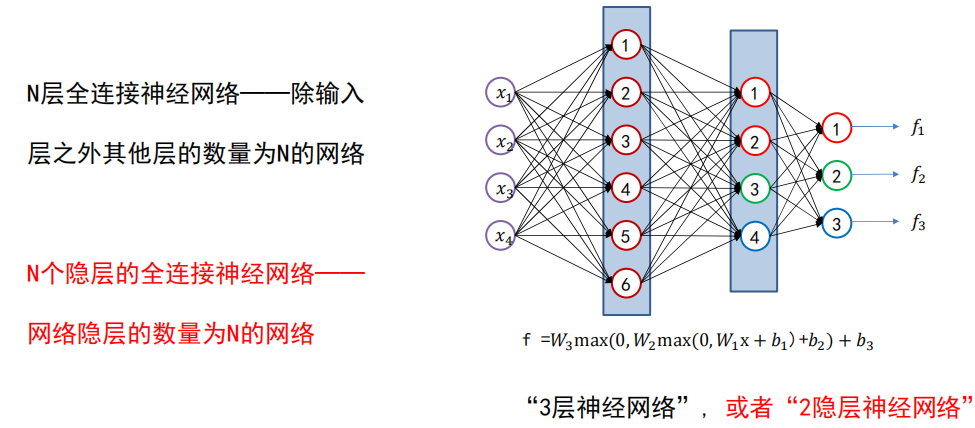
网络结构设计
-
用不用隐层,用一个还是用几个隐层?(深度设计)
-
每隐层设置多少个神经元比较合适?(宽度设计)
没有统一的答案!
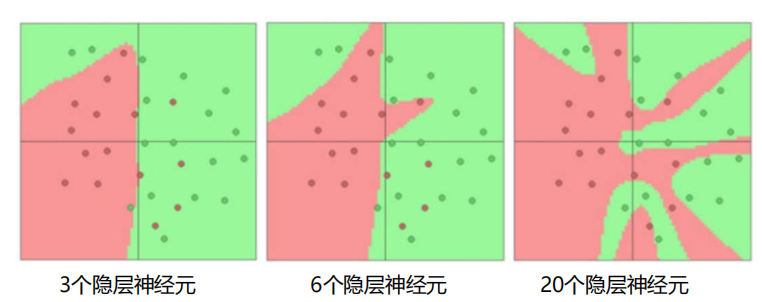
结论:
- 神经元个数越多,分界面就可以越复杂,在这个集合上的分类能力就越强。
依据分类任务的难易程度来调整神经网络模型的复杂程度。
分类任务越难,我们设计的神经网络结构就应该越深、越宽。
但是,需要注意的是对训练集分类精度最高的全连接神经网络模型,在真实场景下识别性能未必是最好的(过拟合) 。
-
4.3 SOFTMAX与交叉熵
-
Softmax
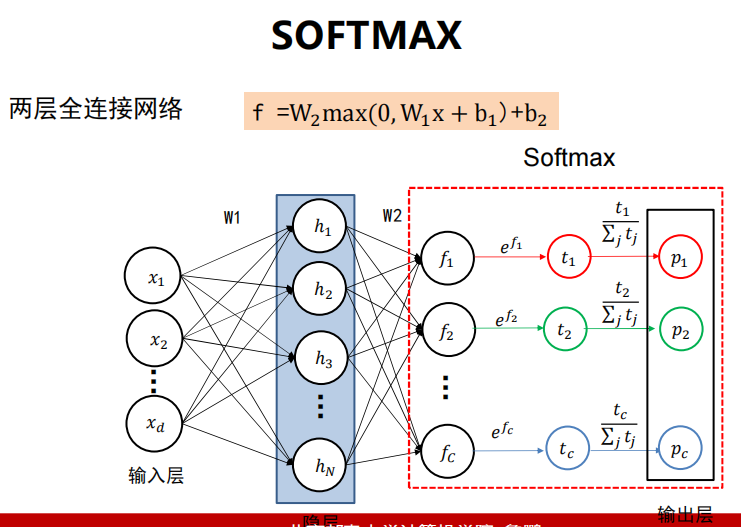

-
交叉熵损失

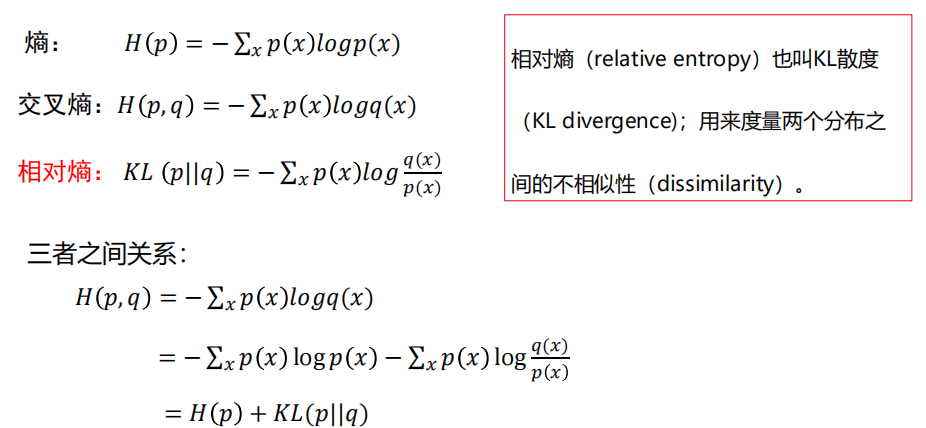

4.4 对比多类支撑向量机损失

问: 相同分数下两种分类器的损失有什么区别?
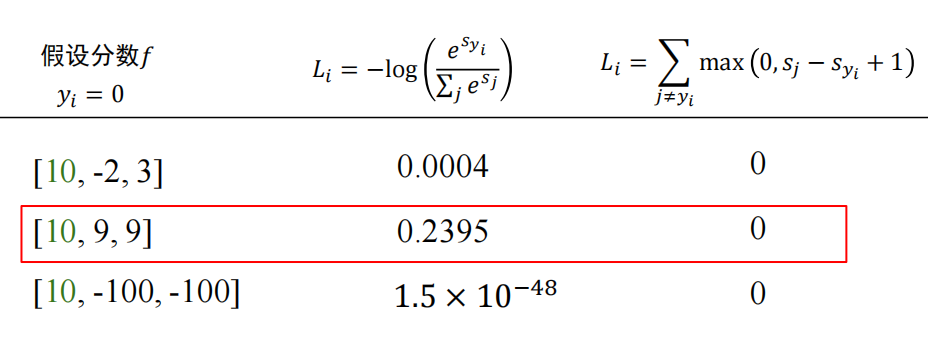
4.5 计算图与反向传播
-
什么是计算图?
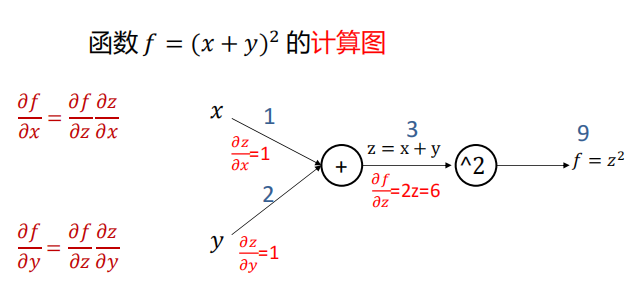
计算图是一种有向图,它用来表达输入、输出以及中间变量之间的计算关系,图中的每个节点对应着一种数学运算。
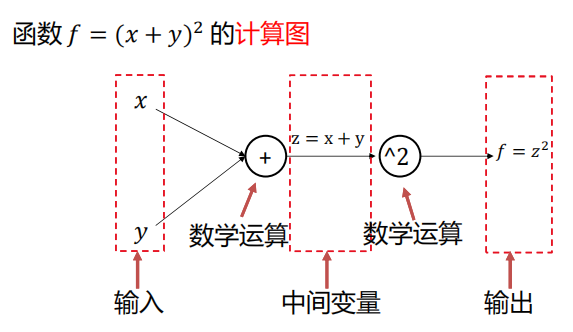
-
任意复杂的函数,都可以用计算图的形式表示
-
在整个计算图中,每个门单元都会得到一些输入,然后,进行下面两个计算:
-
这个门的输出值
-
其输出值关于输入值的局部梯度。
-
-
利用链式法则,门单元应该将回传的梯度乘以它对其的输入的局部梯度,从而得到整个网络的输出对该门单元的每个输入值的梯度。
-
-
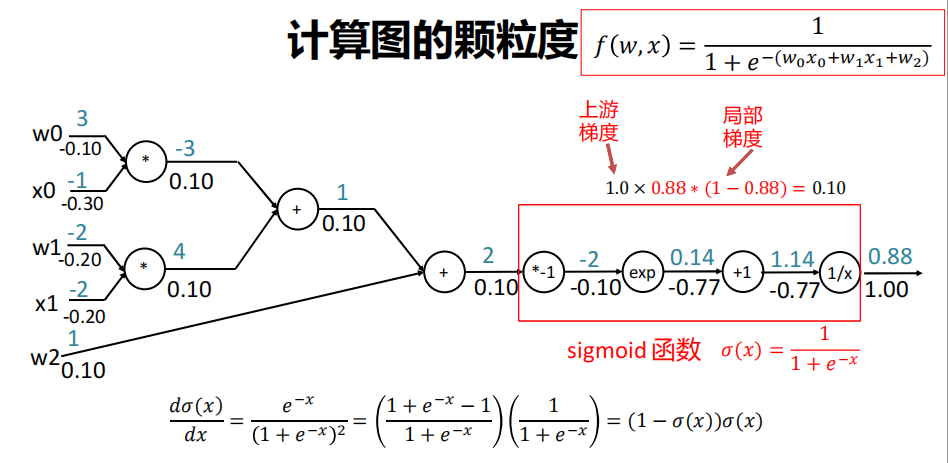
颗粒度
-
常见的门单元
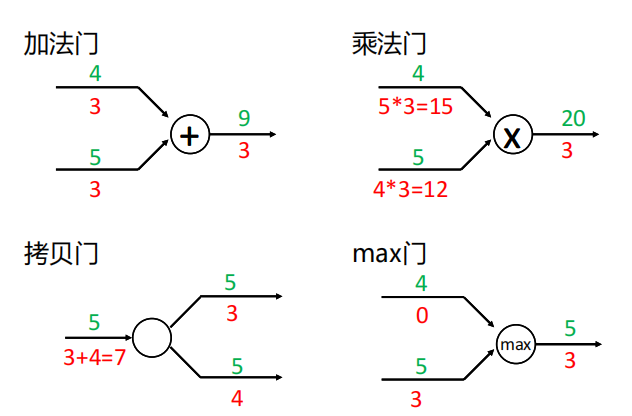
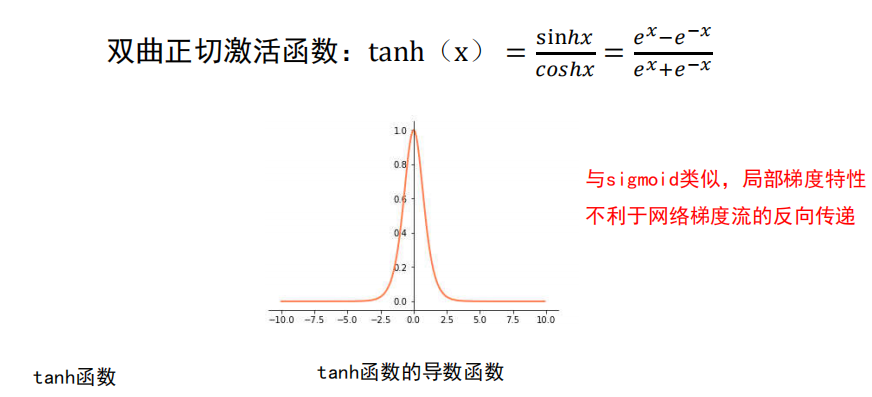
4.6 再谈激活函数
-
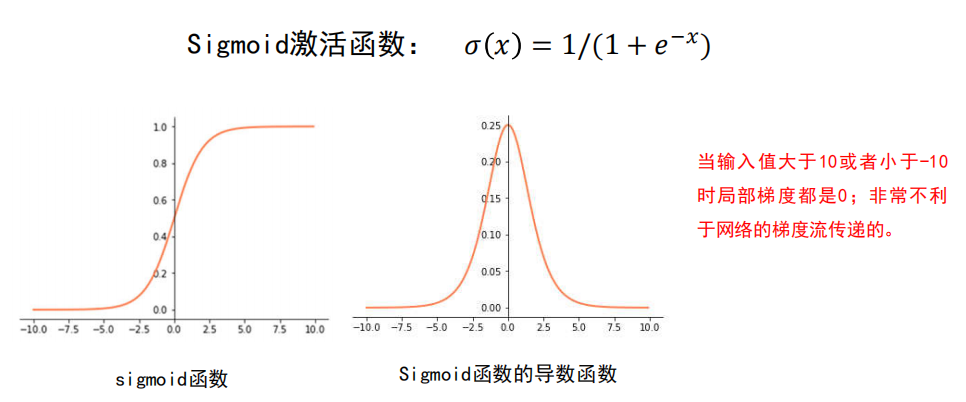
梯度消失
梯度消失是神经网络训练中非常致命的一个问题,其本质是由于链式法则的乘法特性导致的。
-
梯度爆炸
梯度爆炸也是由于链式法则的乘法特性导致的。

-
激活函数选择总结
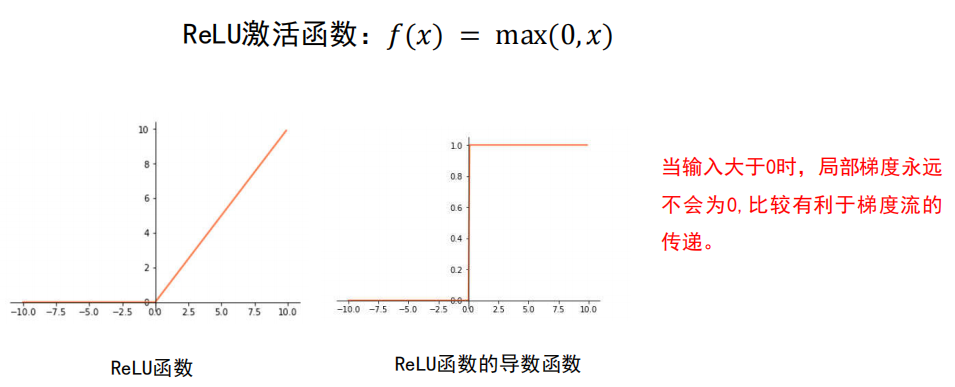
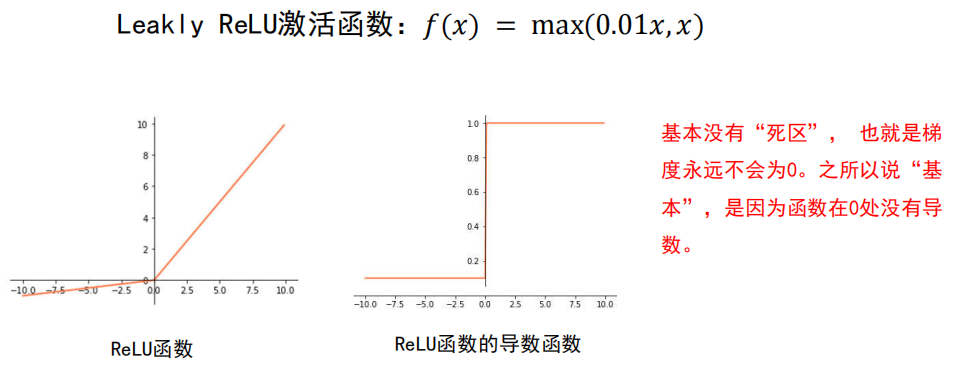
尽量选择 ReLU 函数或者 Leakly ReLU 函数,
相对于Sigmoid/tanh,ReLU函数或者Leakly ReLU函数会让梯度流更加顺畅,训练过程收敛得更快。
4.7 动量法与自适应梯度
-
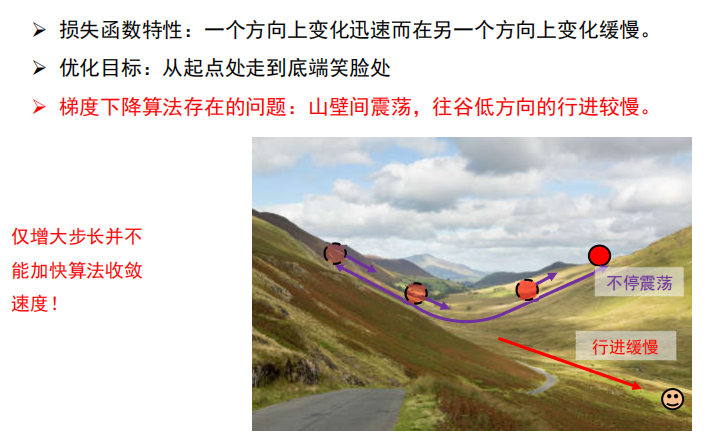
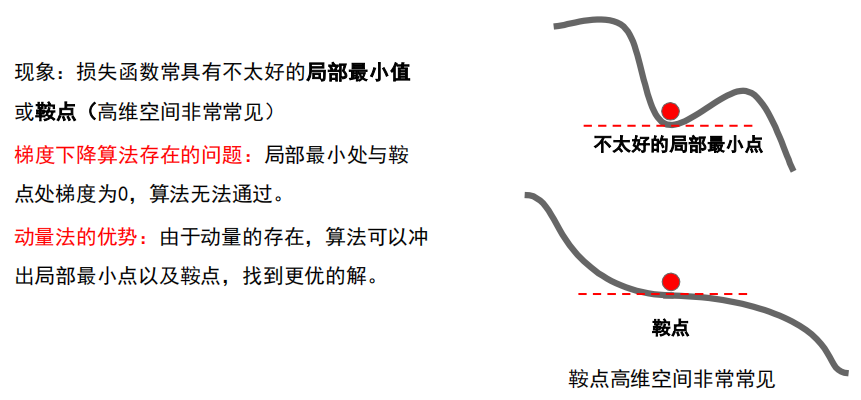
梯度下降算法存在的问题
-
梯度算法改进
(1) 动量法
-
目标
改进梯度下降算法存在的问题,即减少震荡,加速通往谷低
-
改进思想
利用累加历史梯度信息更新梯度
-
算法

为什么有效?
累加过程中震荡方向相互抵消,平坦方向得到加强。
动量法还有什么效果?
(2) 自适应梯度与RMSProp
-
思想
自适应梯度法通过减小震荡方向步长,增大平坦方向步长来减小震荡,加速通往谷底方向
-
如何区分震荡方向与平坦方向?
- 梯度幅度的平方较大的方向是震荡方向
- 梯度幅度的平方较小的方向是平坦方向
-
算法

(3) 结合:ADAM
- 同时使用动量与自适应梯度思想
- 注:修正偏差 步骤可以极大缓解算法初期的冷启动问题

4.8 权值初始化
-
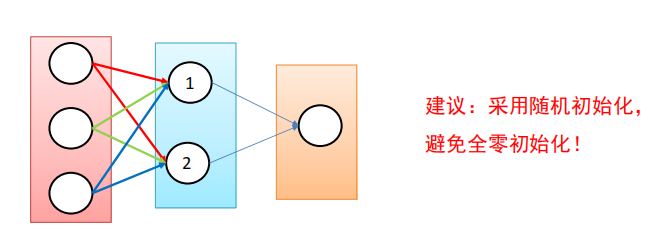
全零初始化
网络中不同的神经元有相同的输出,进行同样的参数更新。
因此,这些神经元学到的参数都一样,等价于一个神经元。
-
随机权值初始化
-
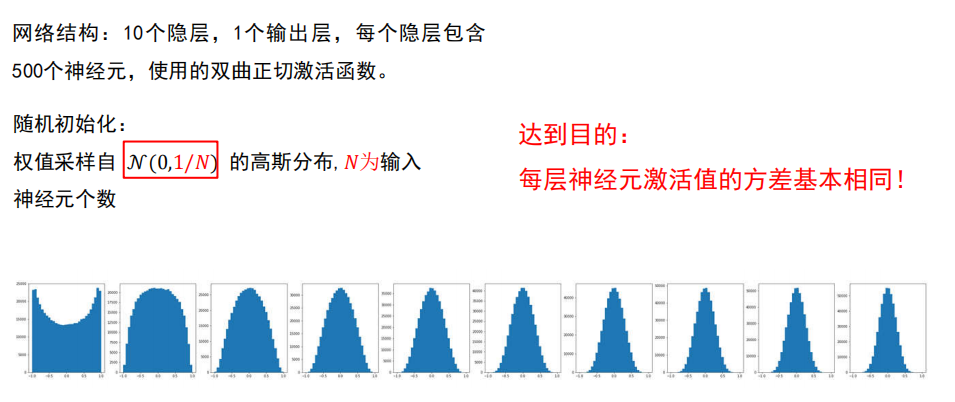
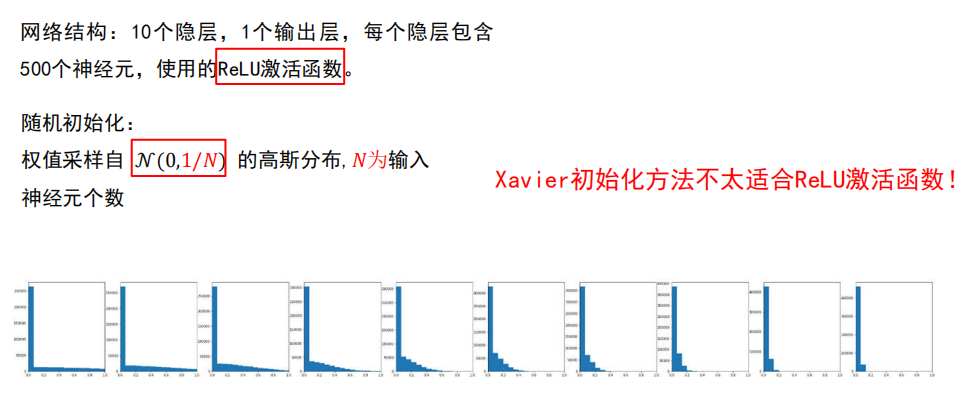
实验:采用不同的高斯分布进行随机


-
实验结论
初始化时只是简单地让权值不相等,并不能保证网络能够正常的被训练。
-
有效的初始化方法
使网络各层的激活值和局部梯度的方差在传播过程中尽量保持一致;
以保持网络中正向和反向数据流动。
-
-
Xavier初始化

-
对于 双曲正切激活函数
很好!
-
对于 ReLu 激活函数
不好!
-
-
HE初始化
- ReLu 激活函数

-
总结
- 好的初始化方法可以防止前向传播过程中的信息消失,也可以解决反向传递过程中的梯度消失。
- 激活函数选择双曲正切或者Sigmoid时,建议使用Xaizer初始化方法;
- 激活函数选择ReLU或Leakly ReLU时,推荐使用He初始化方法
4.9 批归一化
-
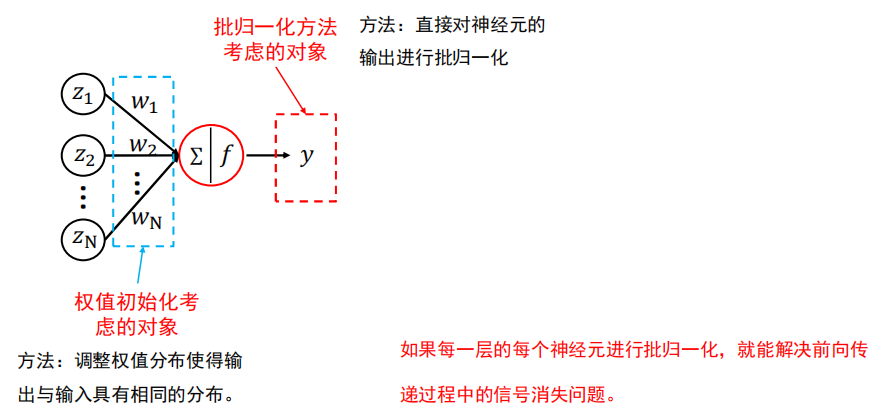
方法
直接对神经元的输出进行批归一化。
如果每一层的每个神经元进行批归一化,就能解决前向传递过程中的信号消失问题。
-
小批量梯度下降算法回顾
每次迭代时会读入一批数据,比如32个样本;
经过当前神经元后会有3个输出值y1,…,y32。
-
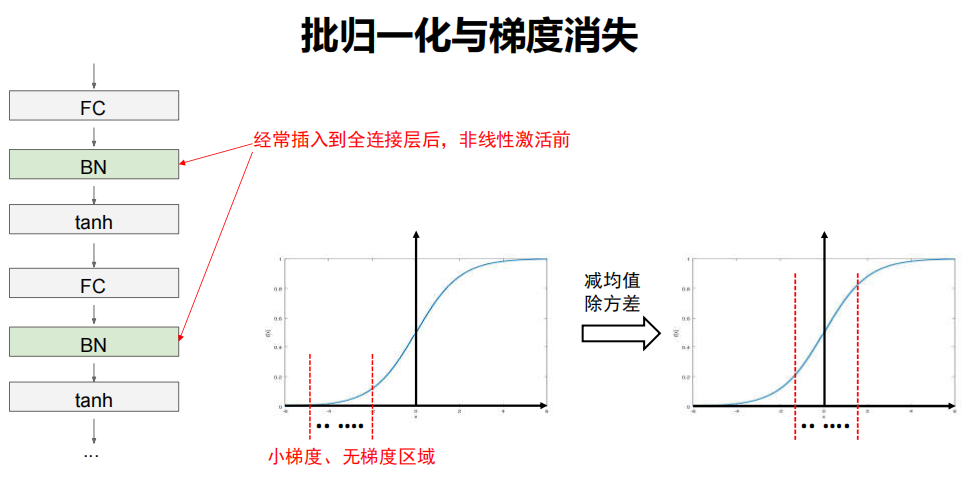
批归一化操作
对这32个输出进行减均值除方差操作;
可保证当前神经元的输出值的分布符合0均值1方差。
-
-
算法

注:这里的 对应前面的 ,只是用 表示。
即,是继续对已经输出的 处理。
-
问题:输出的0均值1方差的正态分布是最有利于网络分类的分布吗?
不一定,所以说,才有“平移缩放”——再次调整方差、均值。
根据对分类的贡献自行决定数据分布的均值与方差。
-
问题:单张样本测试时,均值和方差怎么设置?
来自于训练中。
累加训练时每个批次的均值和方差,最后进行平均,用平均后的结果作为预测时的均值和方差。
-
4.10 欠拟合、过拟合与 Dropout
-
过拟合
是指学习时选择的模型所包含的参数过多,
以至于出现这一模型对已知数据预测的很好,但对未知数据预测得很差的现象。
这种情况下模型可能只是记住了训练集数据,而不是学习到了数据特征。
-
欠拟合
模型描述能力太弱,以至于不能很好地学习到数据中的规律。
产生欠拟合的原因通常是模型过于简单。
-
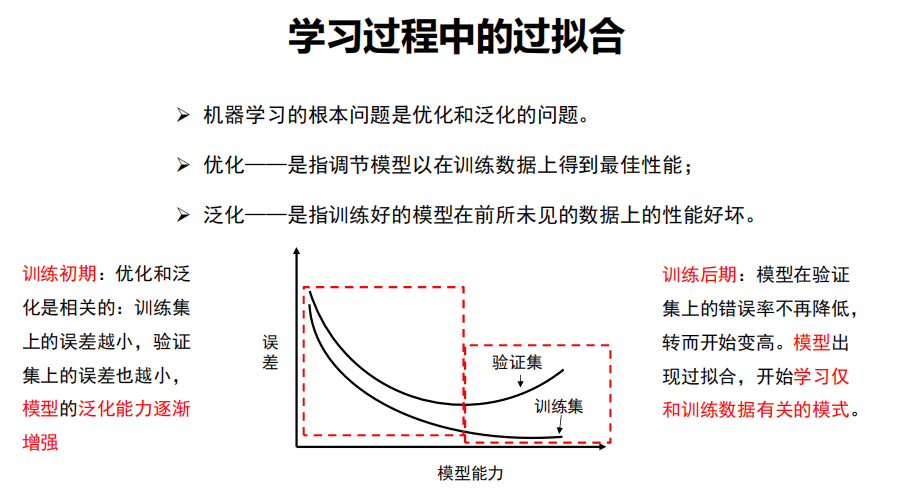
优化、泛化
-
应对过拟合
-
最优方案——获取更多的训练数据
全世界数据都在,就算模型是记住的,那也无所谓。
-
次优方案——调节模型允许存储的信息量或者对模型允许存储的信息加以约束,该类方法也称为正则化。
-
调节模型大小
-
约束模型权重,即权重正则化(常用的有L1、L2正则化)
-
随机失活(Dropout)
-
-
-
L2正则化

-
随机失活(Dropout)
让隐层的神经元以一定的概率不被激活。
-
实现方式
训练过程中,对某一层使用Dropout,就是随机将该层的一些输出舍弃(输出值设置为0),
这些被舍弃的神经元就好像被网络删除了一样。
-
随机失活比率( Dropout ratio)
是被设为 0 的特征所占的比例,通常在 0.2——0.5范围内。

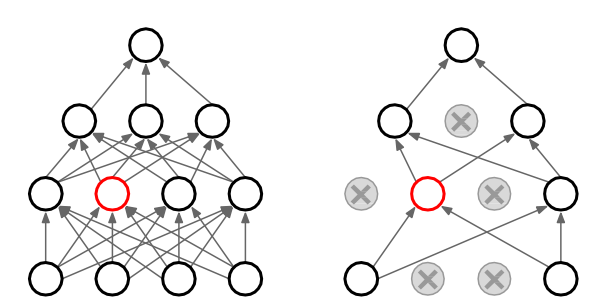
随机失活为什么能够防止过拟合呢?
-
解释1
随机失活使得每次更新梯度时参与计算的网络参数减少了,降低了模型容量,所以能防止过拟合。
-
解释2
随机失活鼓励权重分散,从这个角度来看随机失活也能起到正则化的作用,进而防止过拟合。
-
解释3
Dropout 可以看作是模型集成。
-
4.11 模型正则与超参数调优
-
超参数
- 网络结构——隐层神经元个数,网络层数,非线性单元选择等
- 优化相关——学习率、dropout比率、正则项强度等
超参数的重要性,如何找到合适的超参数?
-
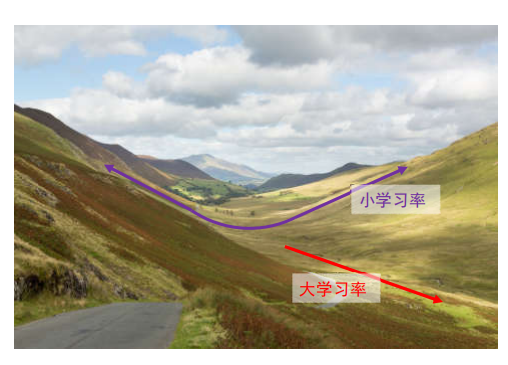
学习率
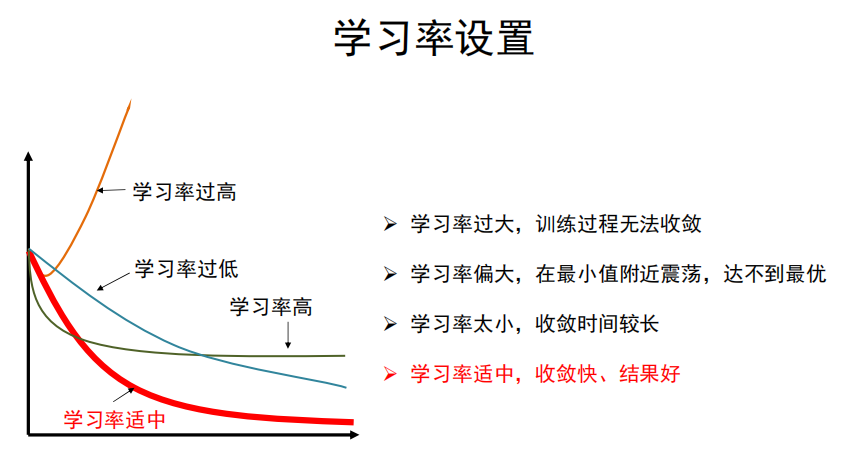
-
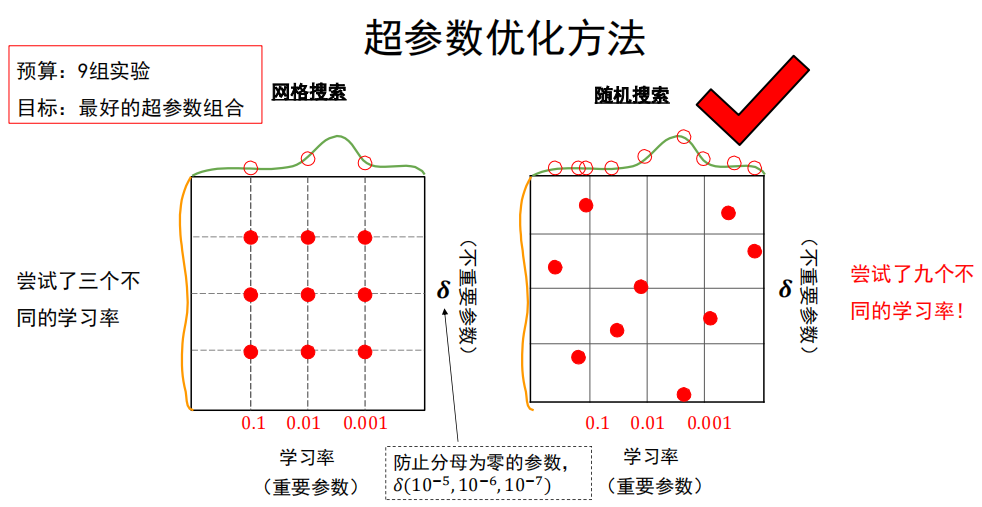
超参数优化方法
-
网格搜索法:
-
每个超参数分别取几个值,组合这些超参数值,形成多组超参数;
-
在验证集上评估每组超参数的模型性能;
-
选择性能最优的模型所采用的那组值作为最终的超参数的值。
-
-
随机搜索法:
-
参数空间内随机取点,每个点对应一组超参数;
-
在验证集上评估每组超参数的模型性能;
-
选择性能最优的模型所采用的那组值作为最终的超参数的值。
-
-
-
超参数搜索策略

-
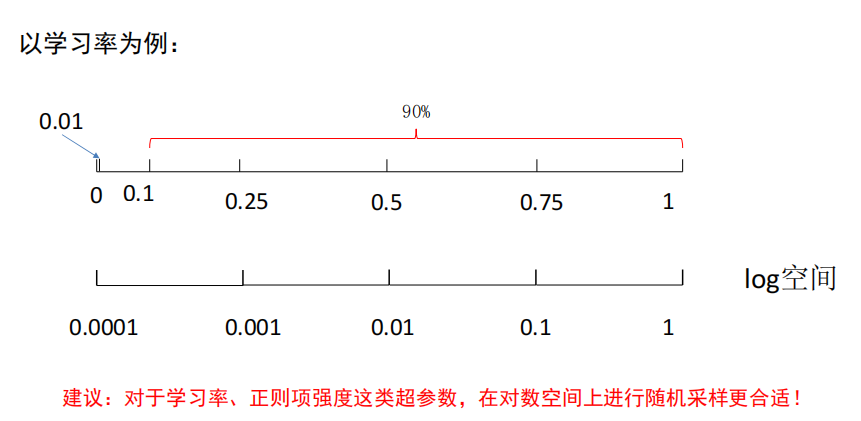
超参数的标尺空间
建议:对于学习率、正则项强度这类超参数,在对数空间上进行随机采样更合适!