五、卷积神经网络

5.0-1 卷积与图像去噪

图像去噪与卷积

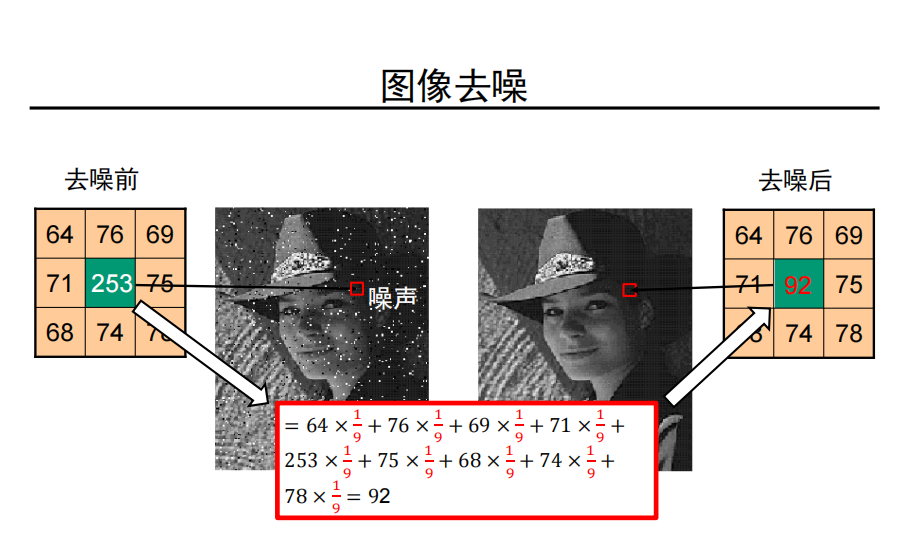
CN-B-1-1

  • 卷积的定义

    令F为图像，H为卷积核，F与H的卷积记为R=F∗HRij=∑u,vHi−u,j−vFu,v令F为图像，H为卷积核，F与H的卷积记为R = F * H \\ R_{ij} = \sum_{u,v} H_{i-u,j-v} F_{u,v}

    本质上，是使用 HH 将 FF 卷积到域 RR 。

  • 卷积性质

    1. 叠加性： filter(f1+f2)=filter(f1)+filter(f2)filter(f_1 + f_2) = filter(f_1) + filter(f_2)
    2. 平移不变性： filter(shift(f))=shift(filter(f))filter(shift(f)) = shift(filter(f))​
    3. 交换律： a∗b=b∗aa*b = b*a​
    4. 结合律：a∗(b∗c)=(a∗b)∗ca*(b*c) = (a*b)*c
    5. 分配律：a∗(b+c)=a∗c+b∗ca*(b+c) = a*c + b*c
    6. 标量：ka∗b=a∗kb=k(a∗b)ka*b = a*kb = k(a*b)

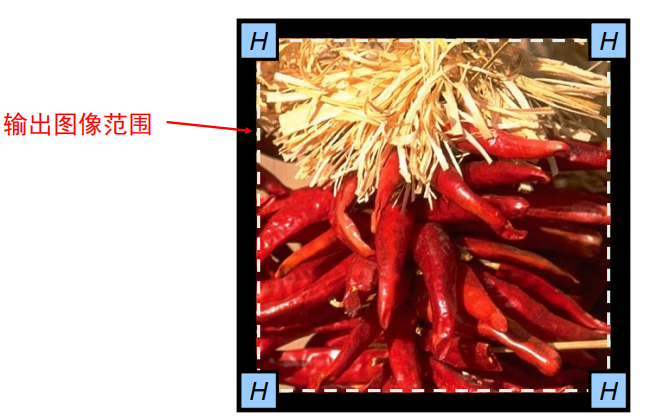
  • 边界填充

    卷积操作后的图像要小于输入时图像，通过边界填充，我们可以实现卷积前后图像的尺寸不变；

    一种最常用的边界填充就是常数填充。

    1. 零填充
    2. 拉伸填充
    3. 镜像填充
    CN-B-1-2 CN-B-1-3

  • 卷积示例

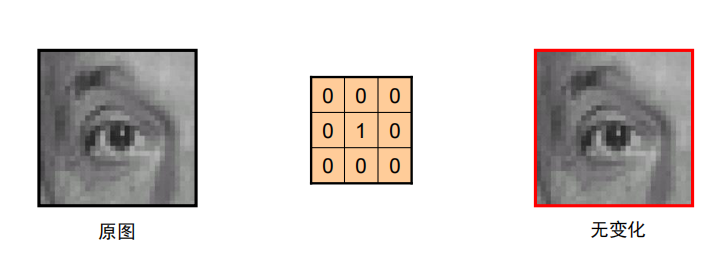
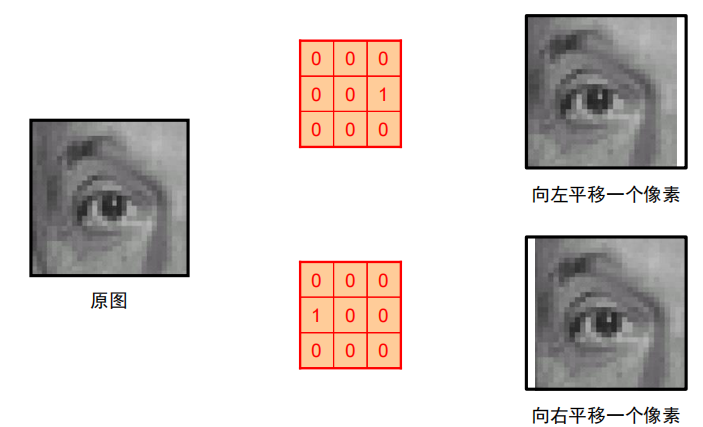
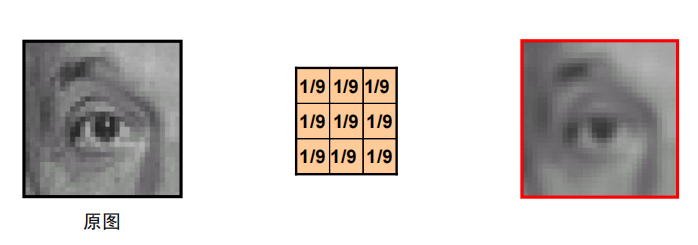
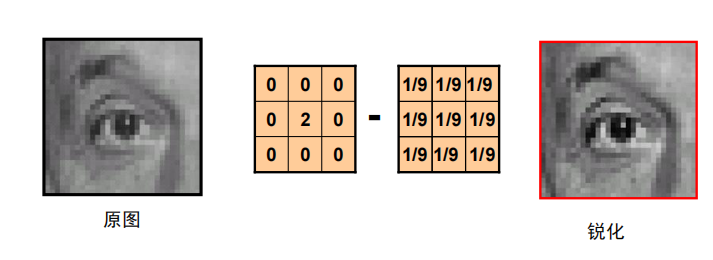
    CN-B-1-4 CN-B-1-5 CN-B-1-6 CN-B-1-7

  • 锐化

    CN-B-1-8

    解析：

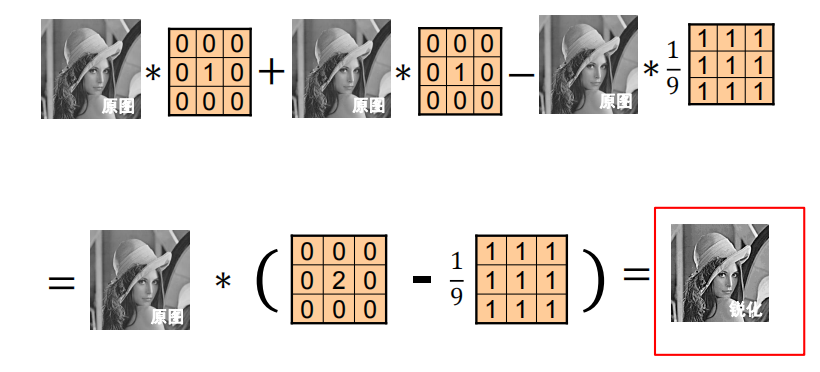
    CN-B-1-9

  • 总结

    卷积是图像处理中的一个基础而又重要的图像操作，它可以实现:

    • 平移
    • 平滑
    • 锐化
    • …

高斯卷积核

  • 平均卷积核存在的问题

    卷积后的图像产生了一些水平和竖直方向的条状

    振铃!

    CN-B-2-1

  • 解决方法

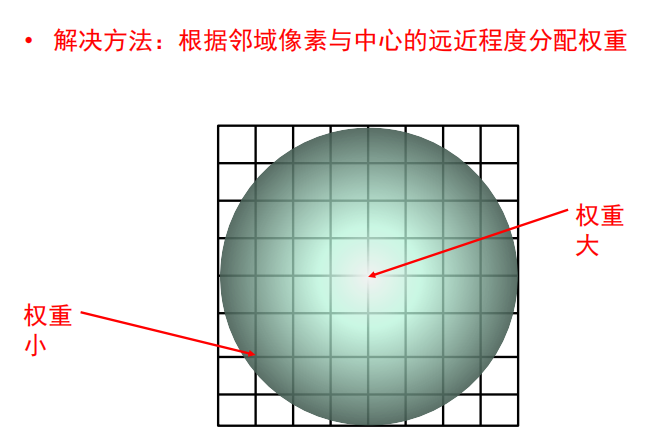
    CN-B-2-2

  • 高斯卷积核

    Gσ=12πσ2e−(x2+y2)2σ2G_{\sigma} = \frac{1}{2 \pi \sigma^2}e^{-\frac{(x^2+y^2)}{2\sigma^2}}​

    高斯卷积核，它能够有效地抑制噪声、实现图像平滑。

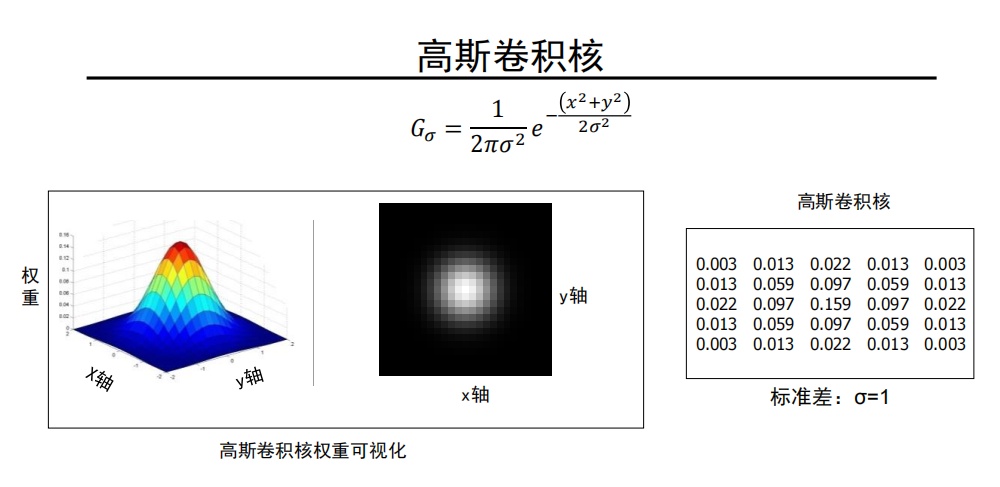
    CN-B-2-3 CN-B-2-4

    如何设置下述参数：

    1. 卷积核的尺寸
    2. 高斯函数的标准差
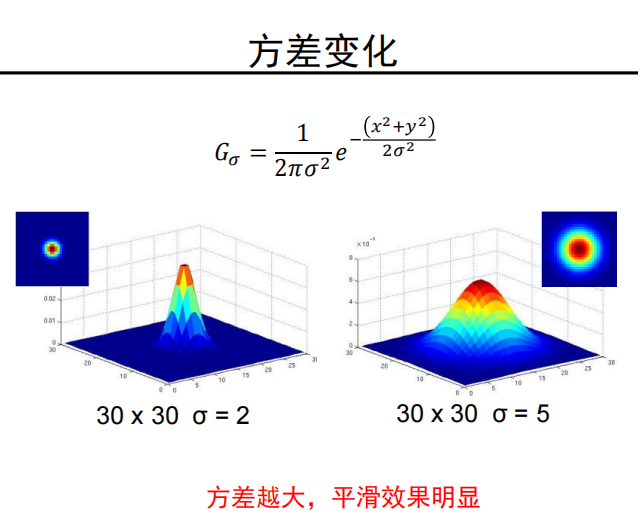
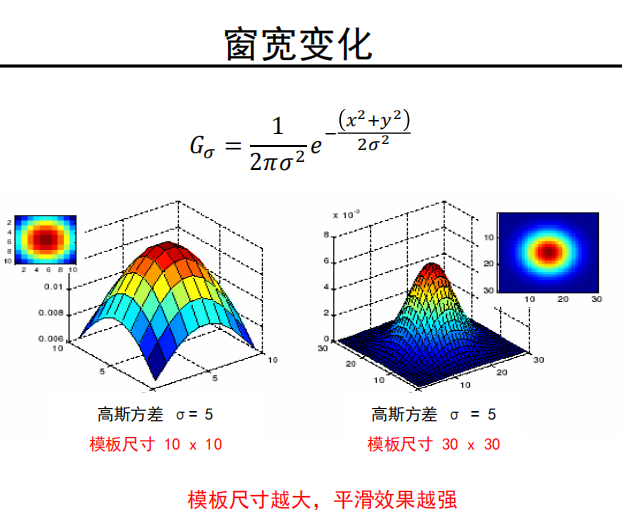
    CN-B-2-5 CN-B-2-6

  • 卷积核参数

    • 大方差或者大尺寸卷积核平滑能力强；

    • 小方差或者小尺寸卷积核平滑能力弱；

    • 经验法则

      将卷积核的半窗宽度设置为 σ\sigma，最终卷积模板尺寸为 2×3σ+12 \times 3 \sigma +1。

    例子：标准差设置成1， 卷积模板宽度=2∗3∗1+1=72*3*1 + 1 = 7

  • 高斯卷积核 vs.平均卷积核

    CN-B-2-7

    效果：

    • 去除图像中的“高频”成分（低通滤波器）

    • 两个高斯卷积核卷积后得到的还是高斯卷积核

      • 使用多次小方差卷积核连续卷积，可以得到与大方差卷积核相同的结果
      • 使用标准差为 σ\sigma 的高斯核进行两次卷积与使用标准差 σ2\sigma \sqrt{2} 的高斯核进行一次卷积相同

    • 可分离

      • 可分解为两个一维高斯的乘积
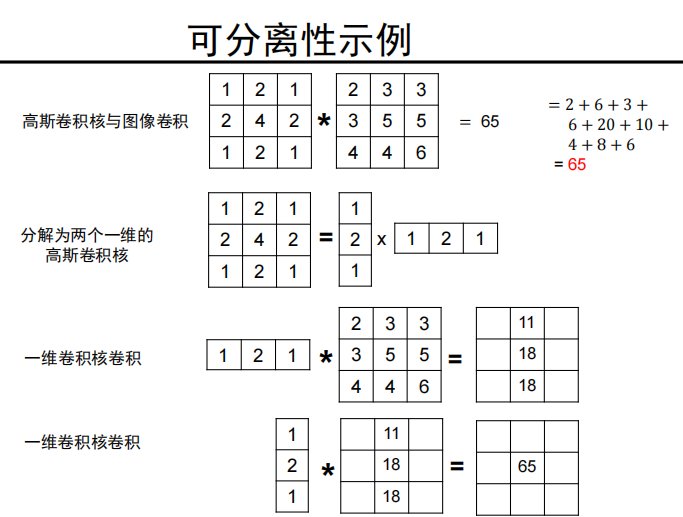
      CN-B-2-8

  • 卷积操作运算量

    1. 用尺寸为 m×mm\times m 的卷积核卷积一个尺寸为 n×nn\times n​ 的图像，其计算复杂度是多少?

      答：O(n2m2)O(n^2m^2)

    2. 如果核可分离呢?

      答：O(n2m)O(n^2m)​

  • 高斯卷积核的堆叠以及分解，它们都可以用于减少卷积计算的复杂度。

图像噪声与中值滤波器

  • 前面都是高斯噪声：
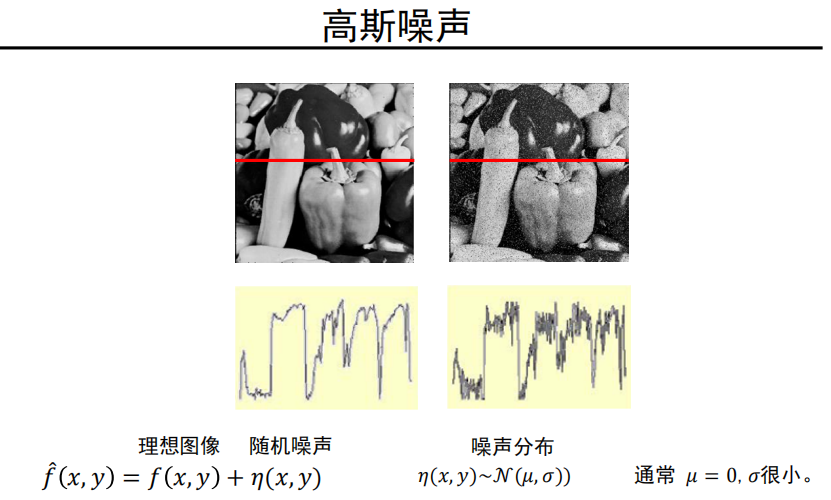
CN-B-3-1 CN-B-3-2

  • 噪声

    • 椒盐噪声: 黑色像素和白色像素随机出现
    • 脉冲噪声: 白色像素随机出现
    • 高斯噪声: 噪声强度变化服从高斯分布（正态分布）
    CN-B-3-3

  • 若是仍然采用高斯卷积核：

    CN-B-3-4

    效果不佳。

  • 采用 中值滤波：

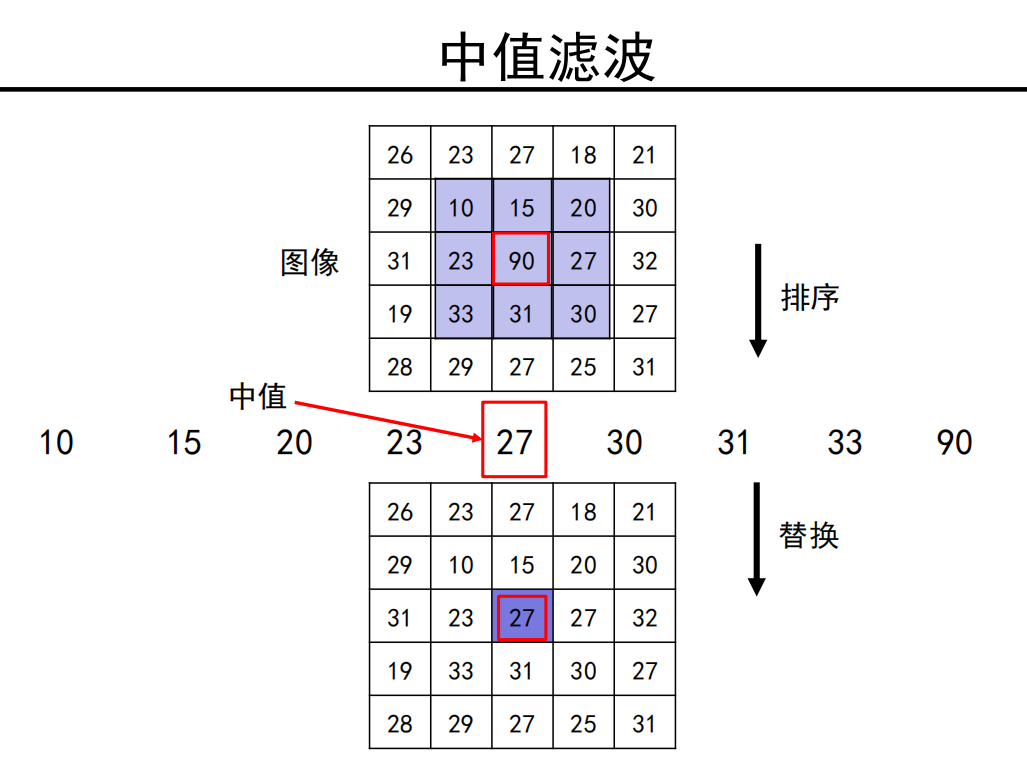
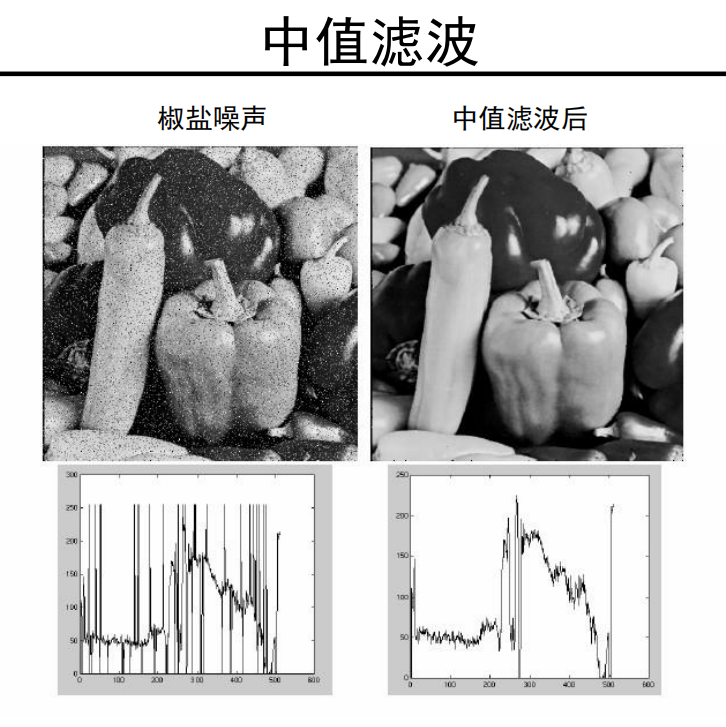
    CN-B-3-5 CN-B-3-6

    中值滤波 效果明显更好！

    • 椒盐噪声、脉冲噪声：中值滤波
    • 高斯噪声：高斯卷积核

5.0-2 卷积与边缘提取

CN-C-1-0

  • 边缘

    图像中亮度明显而急剧变化的点

  • 为什么要研究边缘？

    • 编码图像中的语义与形状信息

    • 相对于像素表示，边缘表示显然更加紧凑

  • 边缘的种类

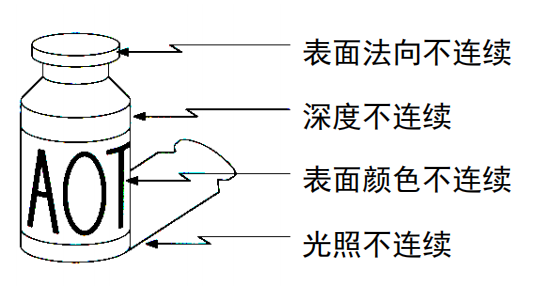
    CN-C-1-1

边缘检测

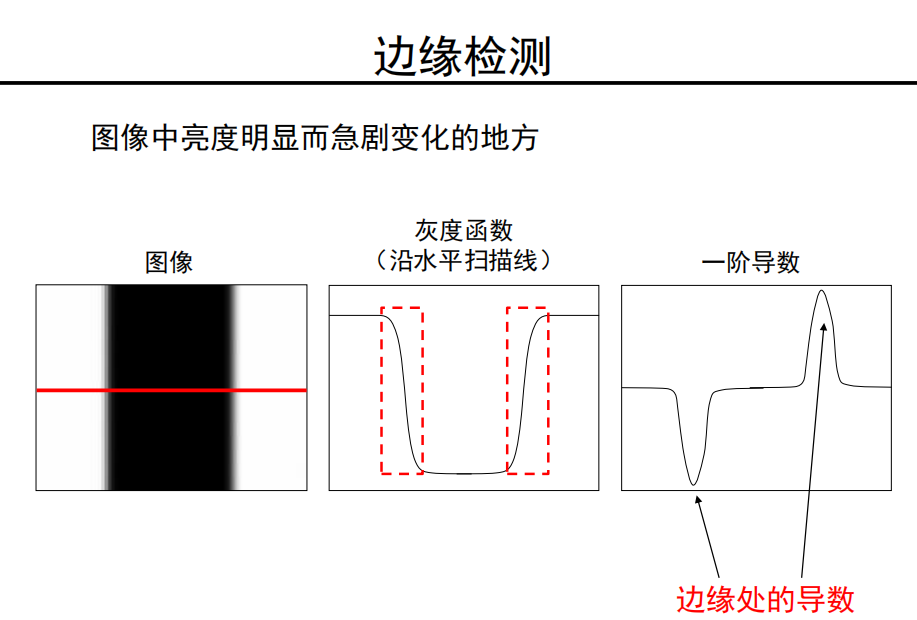
CN-C-1-2

图像求导

CN-C-1-3 CN-C-1-4

图像梯度

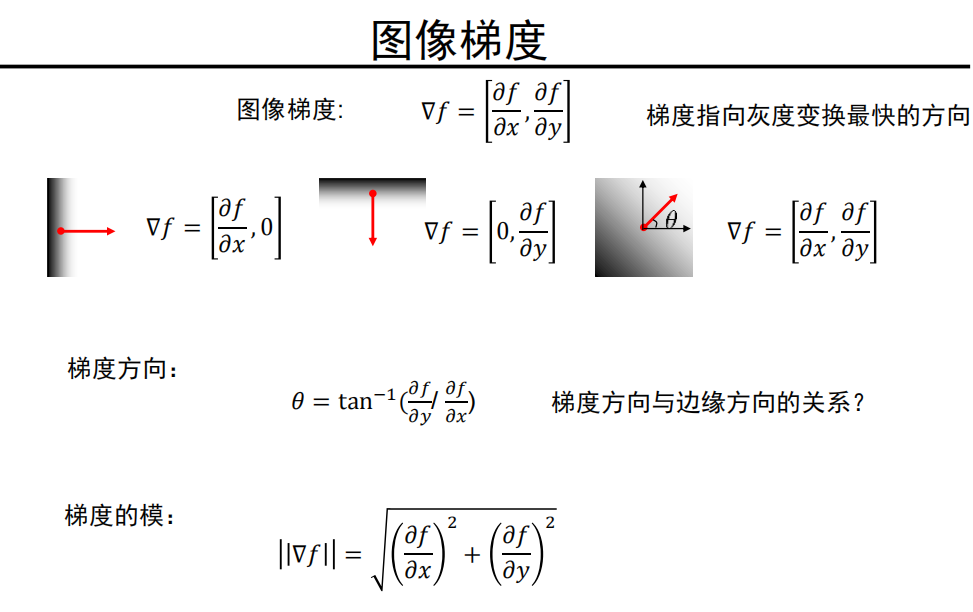
CN-C-1-5

完整示例：

CN-C-1-6

解决流程

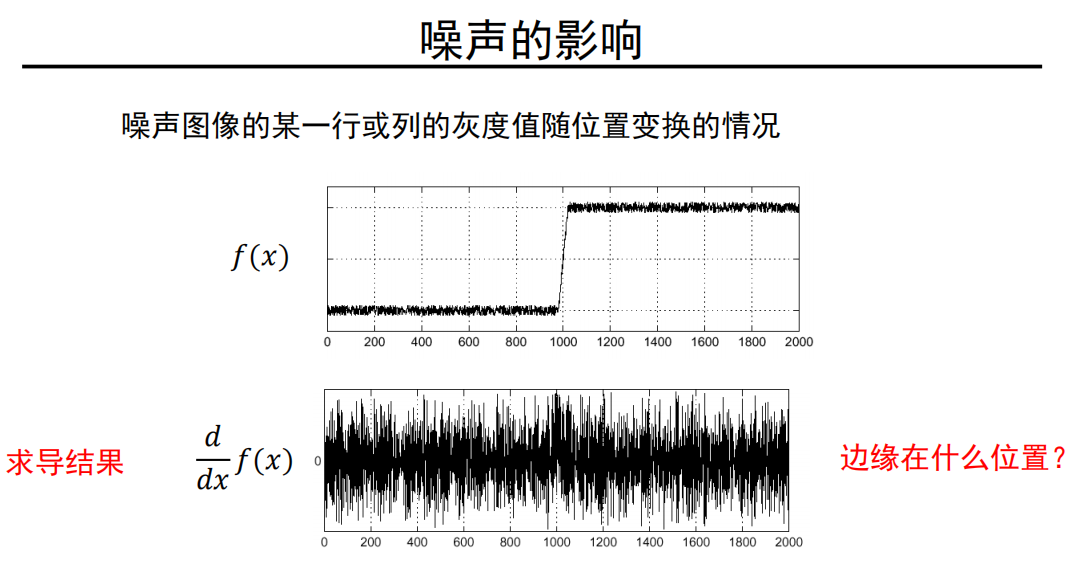
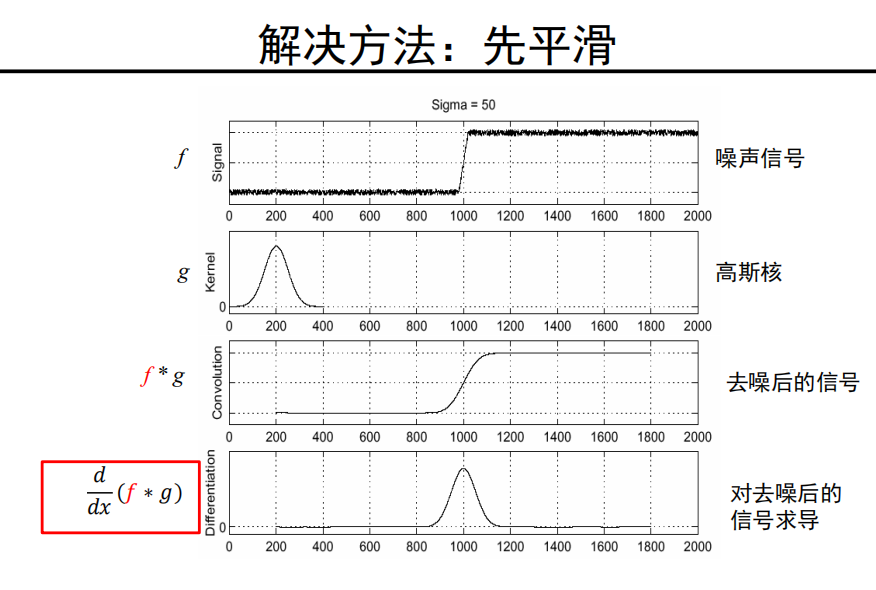
CN-C-1-7 CN-C-1-8

利用卷积的结合性：

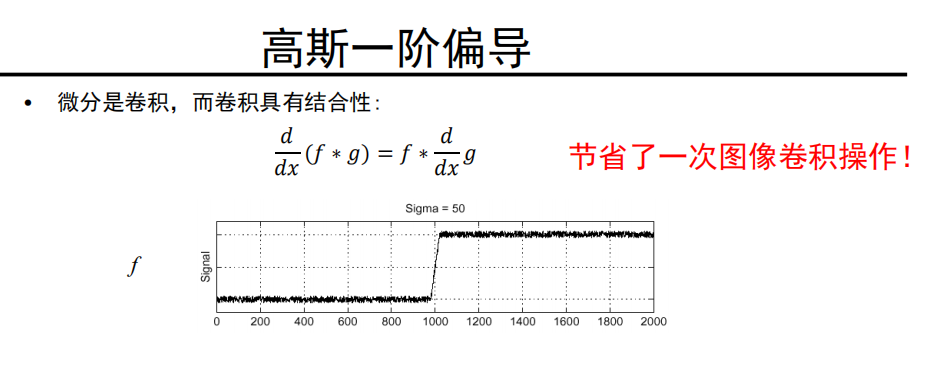
CN-C-1-9

高斯一阶偏导卷积核

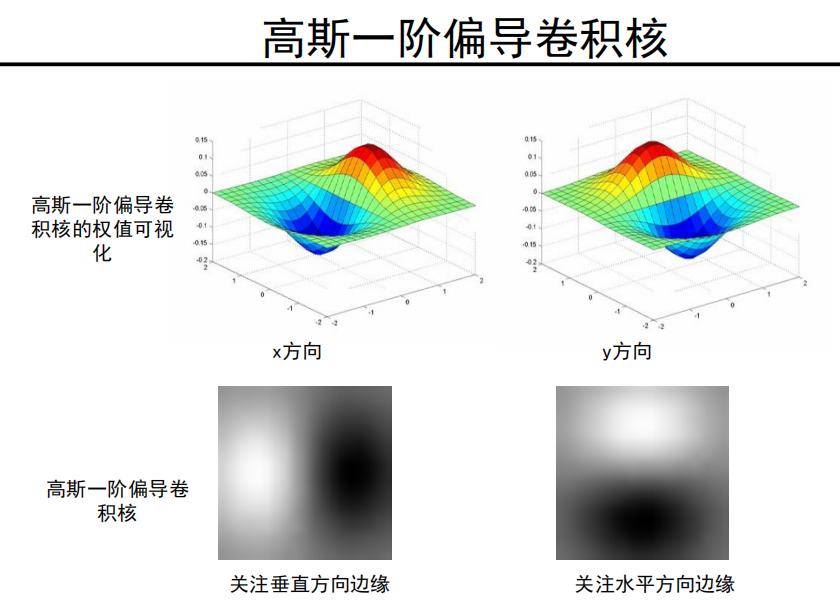
CN-C-2-1
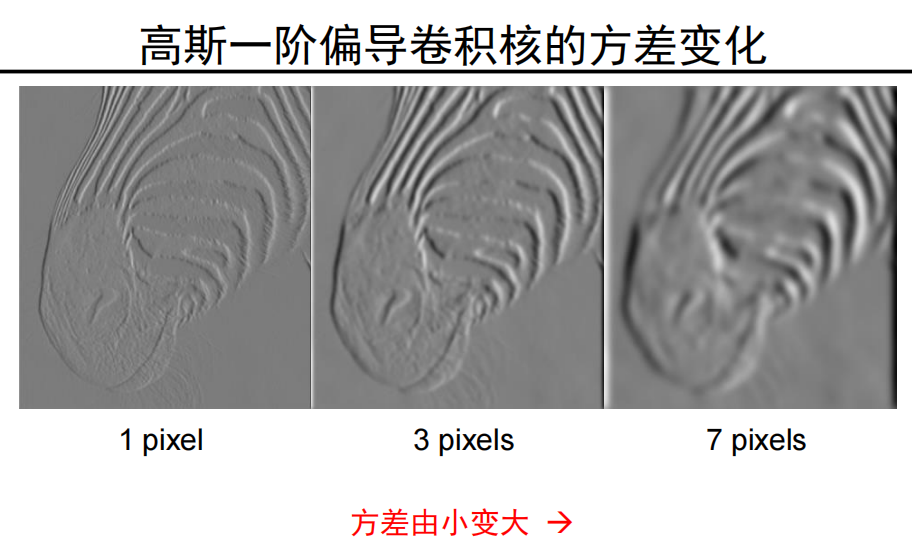
CN-C-2-2

  • 注意：

    这里并不是说变大就更好，也不是更小就更好。

    而是不同的方差会学习到不同的信息，

    • 小方差：关注细节，小范围，如 1pixel 下的胡须都可见
    • 大方差：关注大内容，大范围，如 整个眼睛、鼻子之类的器官会更敏感

  • 高斯核 vs.高斯一阶偏导核

    CN-C-2-3

Canny边缘检测器

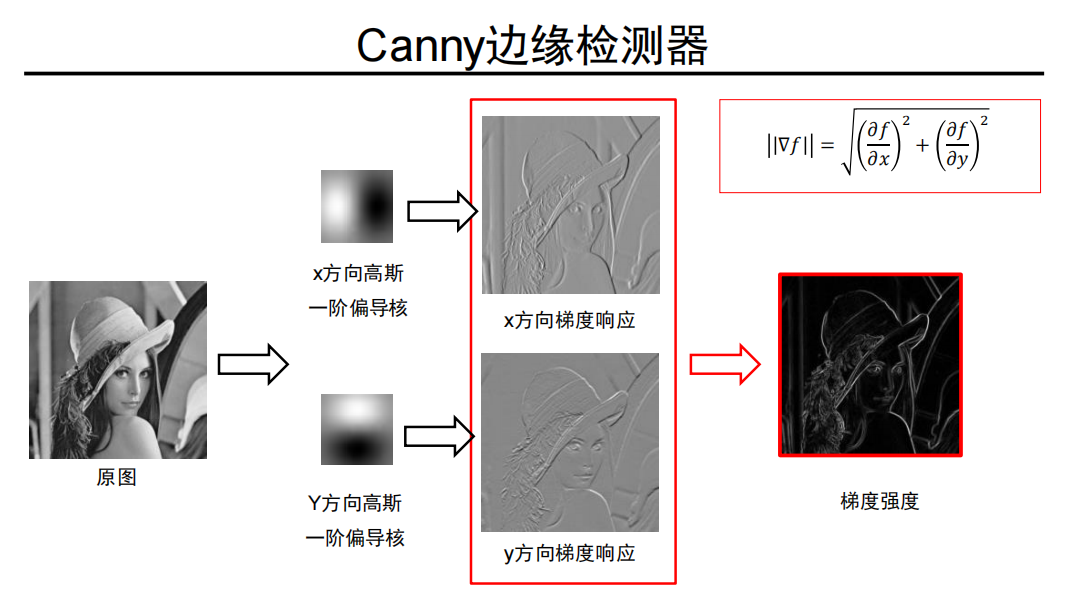
CN-C-2-4

  • 问题：如何得到更为准确的边缘？

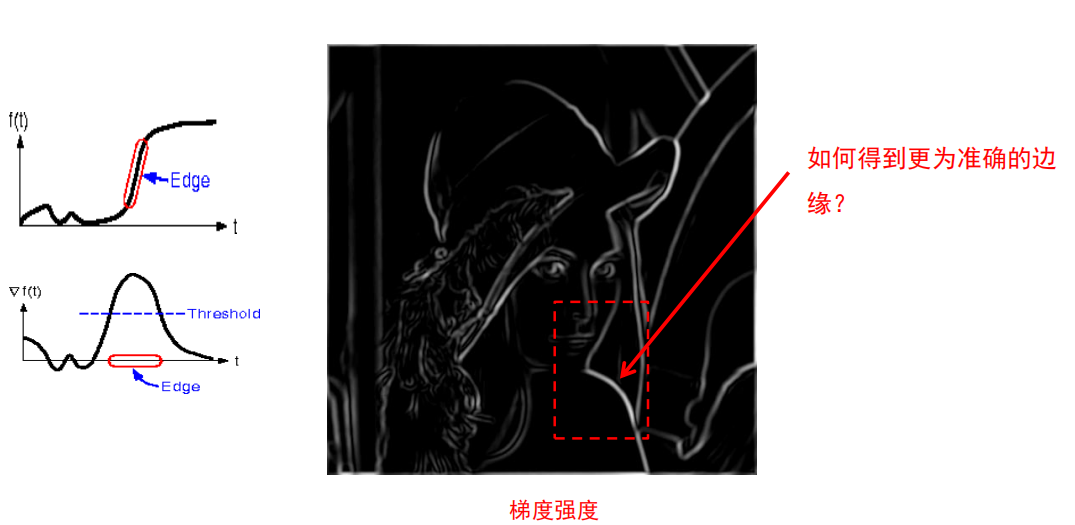
    CN-C-2-5

  • 非最大化抑制

    CN-C-2-6

    效果：

    CN-C-2-7
    • 门限过高：线条断裂
    • 门限过低：线条过多

  • 双阈值

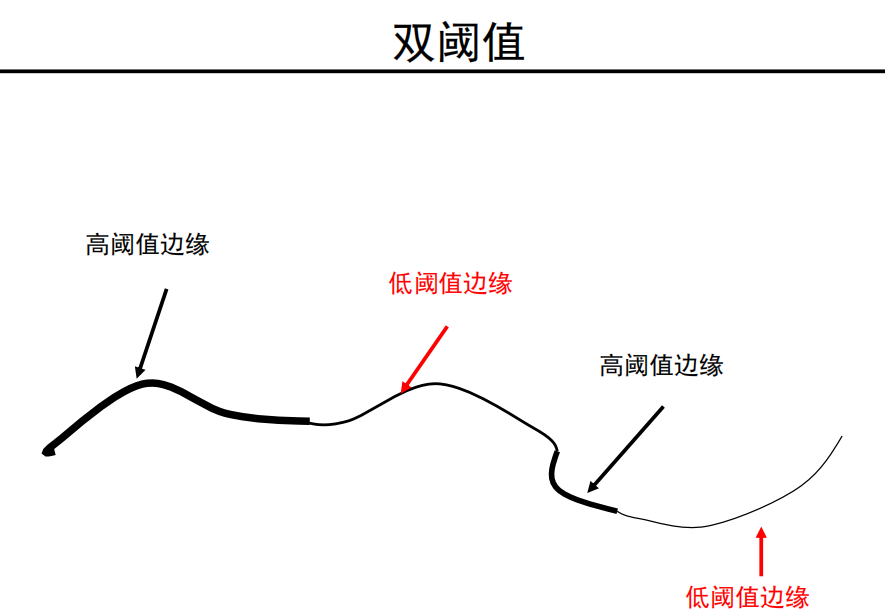
    CN-C-2-8

    双阈值，

    高阈值：均保留

    低阈值：与高阈值边缘 连接的保留，否则丢弃

  • 最终方案

    CN-C-2-9

5.0-3 纹理表示

CN-D-1-1 CN-D-1-2

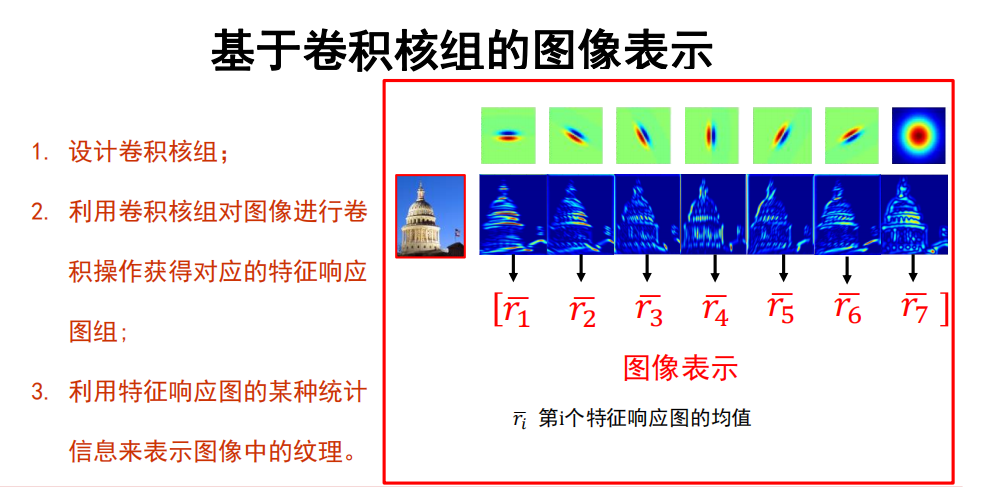
基于卷积核组的纹理表示方法

  • 思路

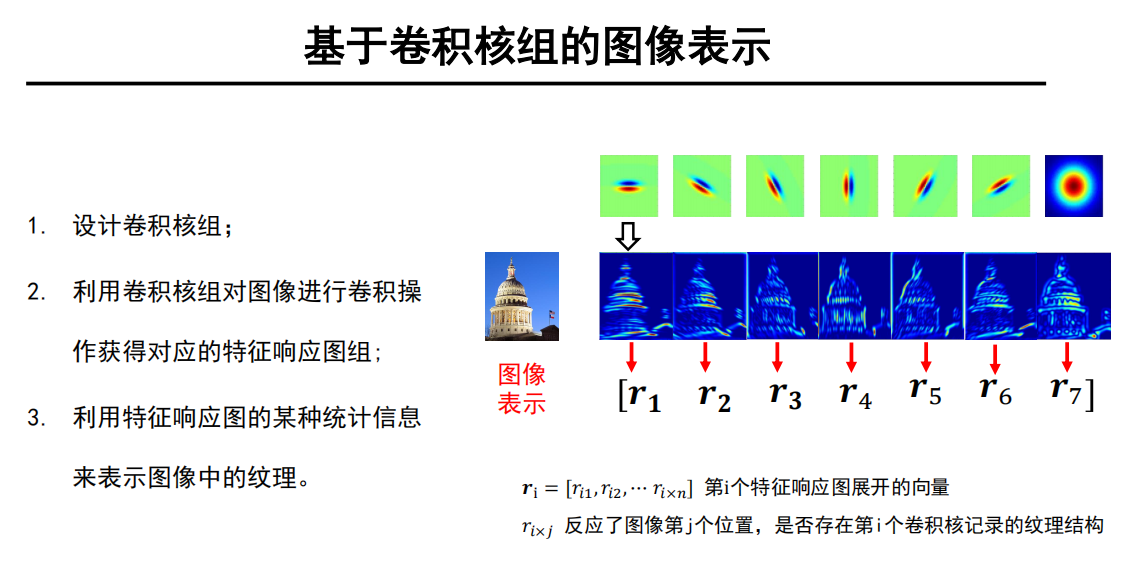
    利用卷积核组提取图像中的纹理基；

    利用基元的统计信息来表示图像中的纹理。

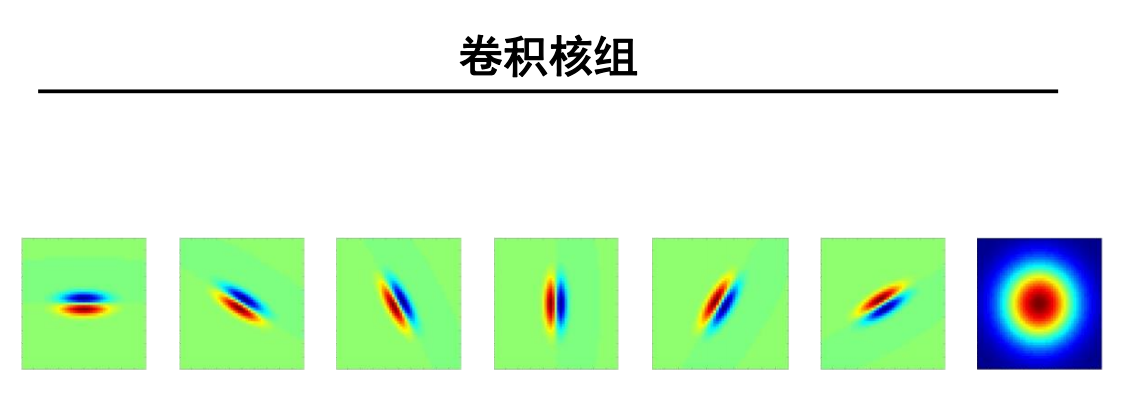
    CN-D-1-3

  • 示例

    CN-D-1-4

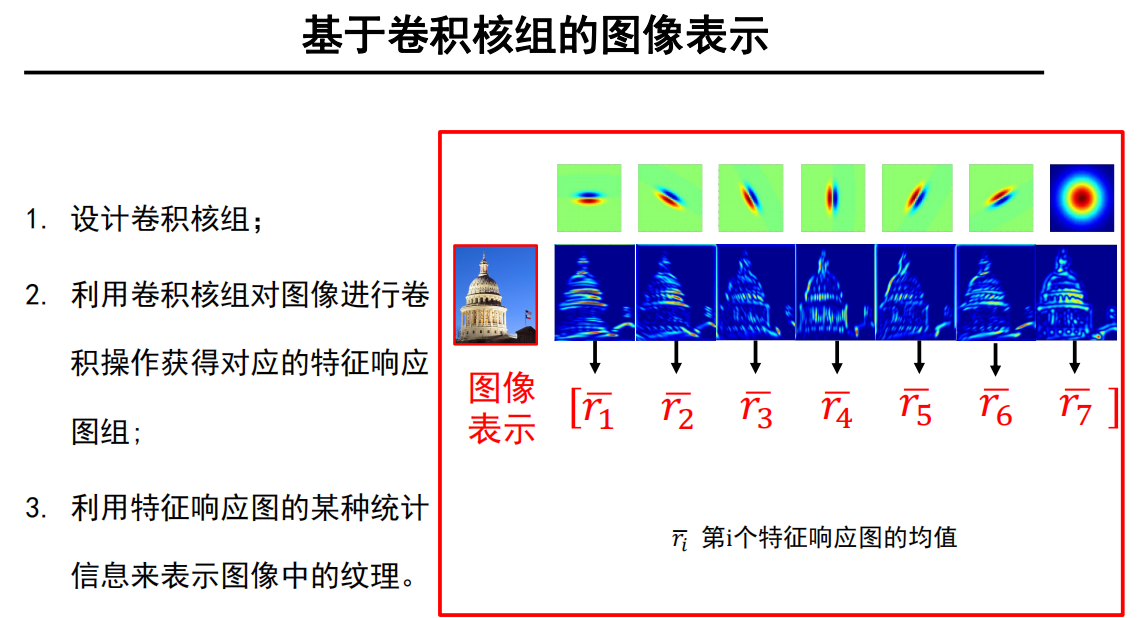
改进图像表示

基于纹理分类任务的特点：

CN-D-1-5

由于并不需要关注基元位置信息，

只需要关注有没有出现，因此可以改进为 均值。

CN-D-1-6

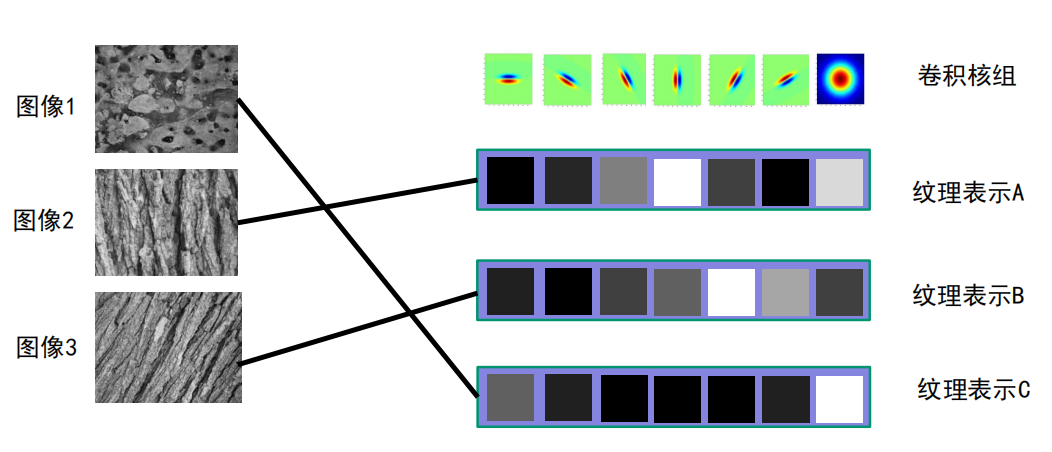
小游戏：

CN-D-1-7

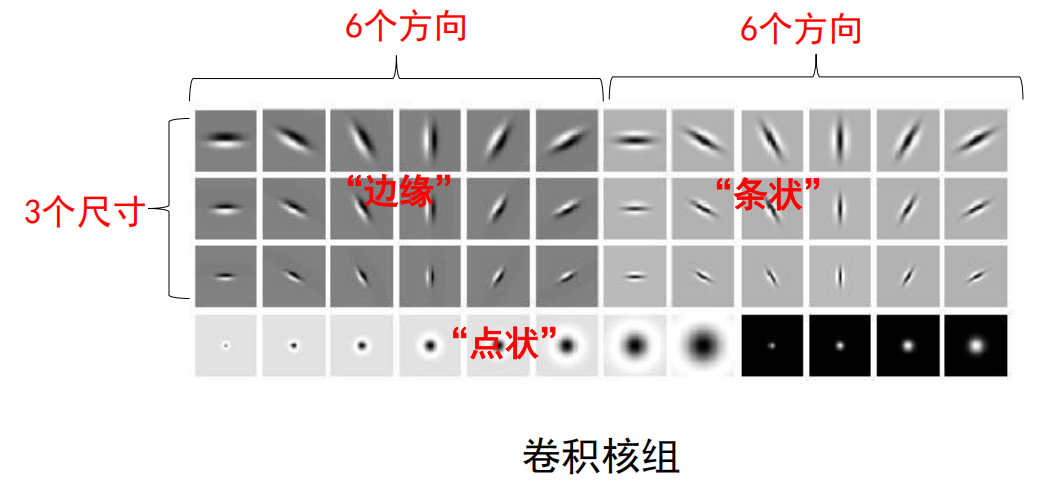
卷积核组设计

  • 设计重点：
    • 卷积核类型（边缘、条形以及点状）
    • 卷积核尺度（3-6个尺度）
    • 卷积核方向（6个角度）
CN-D-2-1

实际例子：

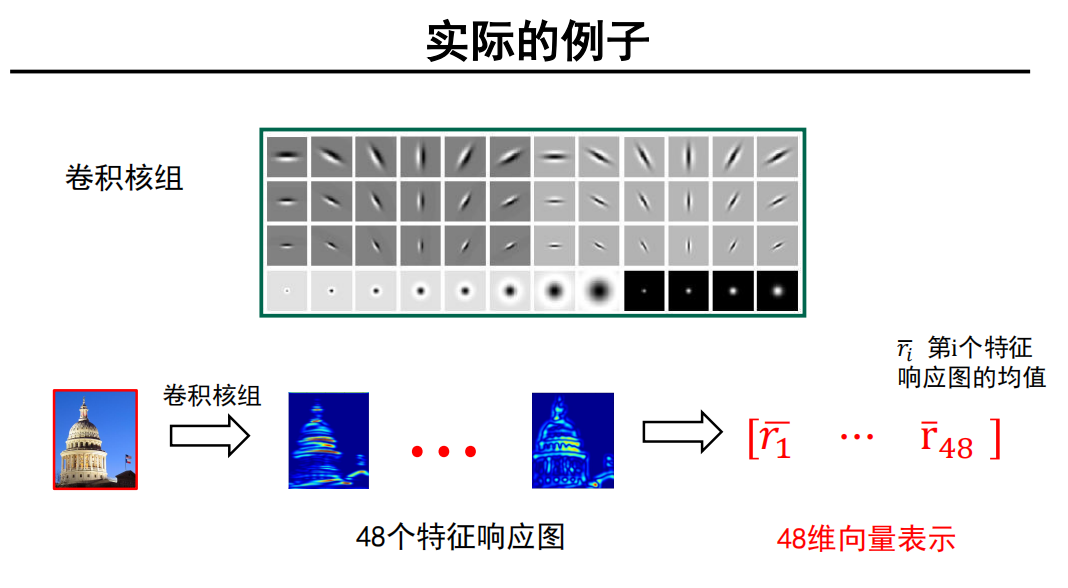
CN-D-2-2

总结

  1. 设计卷积核组；
  2. 利用卷积核组对图像进行卷积操作获得对应的特征响应图组;
  3. 利用特征响应图的某种统计信息来表示图像中的纹理。

5.0 整体框架

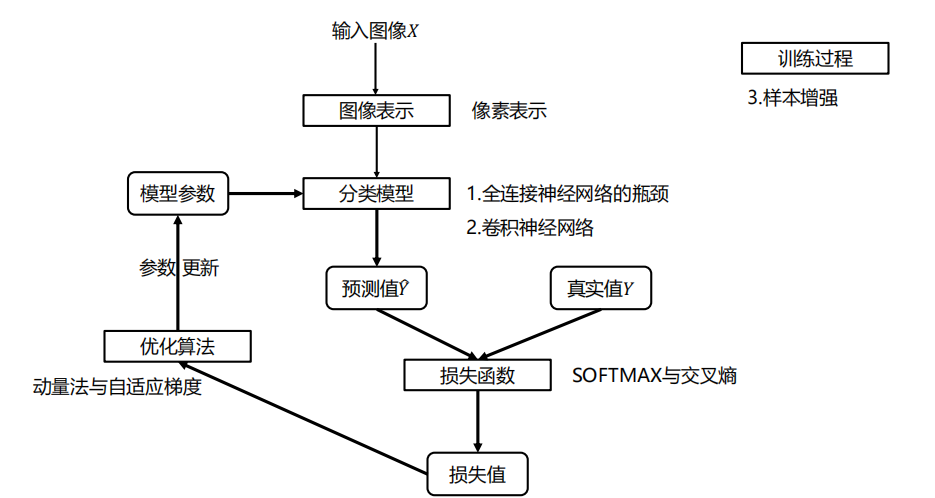
CN-E-1-1

图像表示还是一样：

CN-E-1-2

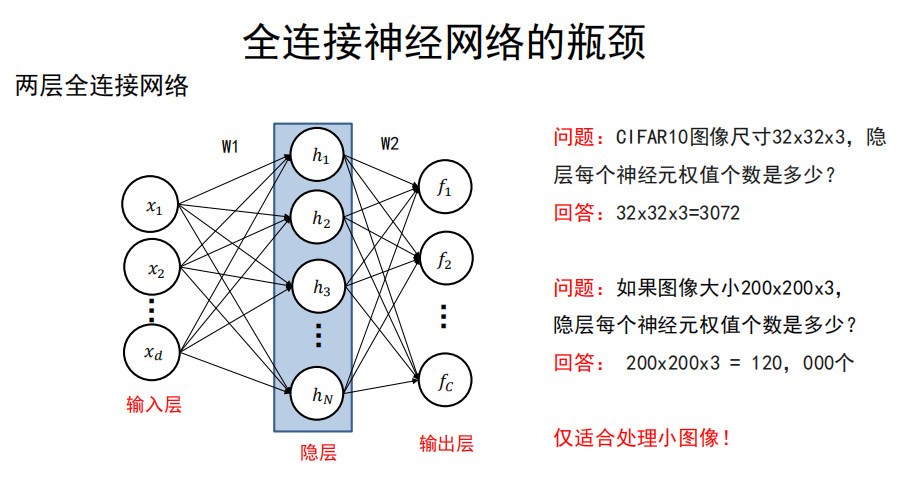
5.1 全连接神经网络的瓶颈

  • 仅适合处理小图像！

    否则，计算量爆炸！

CN-E-2-1

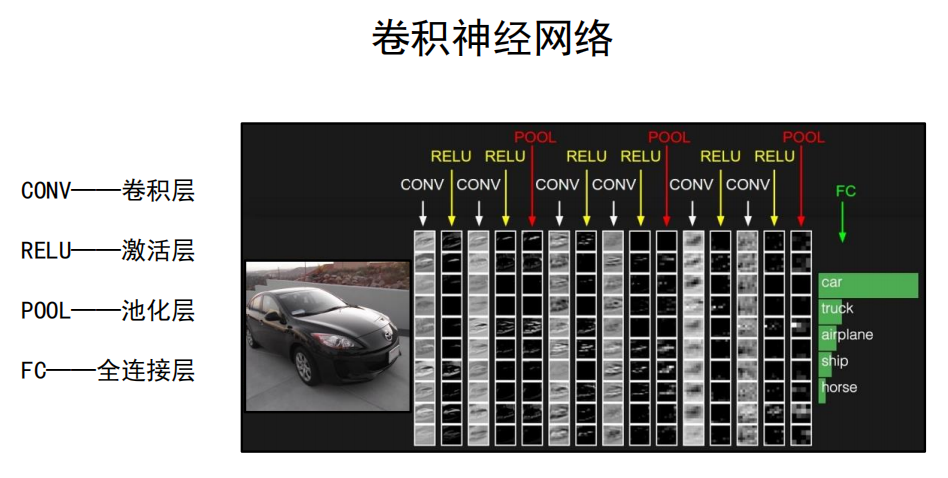
5.2 卷积神经网络

  • 各层次：
    • CONV——卷积层
    • RELU——激活层
    • POOL——池化层
    • FC——全连接层
CN-E-2-2

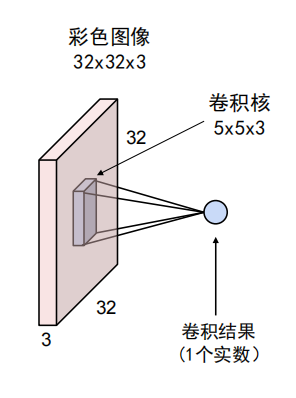
卷积层 CONV

CN-E-2-3

  • 卷积层中的卷积核

    1. 不仅具有宽和高，还具有深度，常写成如下形式：

    W×H×DW \times H \times D

    1. 卷积核参数不仅包括核中存储的权值，还包括一个偏置值。

  • 卷积计算过程

    1. 将卷积核展成一个5x5x3的向量，同时将其覆盖的图像区域按相同的展开方式展成5x5x3的向量
    2. 计算两者的点乘。
    3. 在点乘的结果上加上偏移量。

  • 数学公式

    wTx+bw为卷积核的权值，b为卷积核的偏置。w^T x + b \\ w 为卷积核的权值，b为卷积核的偏置。

    CN-E-2-4

  • 特征响应图

    特征响应图中每个位置上的值反映了图像上对应位置是否存在卷积核所记录的基元结构信息。

  • 卷积层

    使用多个卷积核，就是整个卷积层做的事情。

    CN-E-2-5
    • 特征响应图组深度等于卷积核的个数；
    • 不同的特征响应图反映了输入图像对不同卷积核的响应结果；
    • 同一特征响应图上不同位置的值表示输入图像上不同位置对同一卷积核的响应结果。

    注意：

    卷积层输入不局限于图像，可以是任意三维数据矩阵;

    该层的卷积核深度要求与输入的三维矩阵的深度一致。

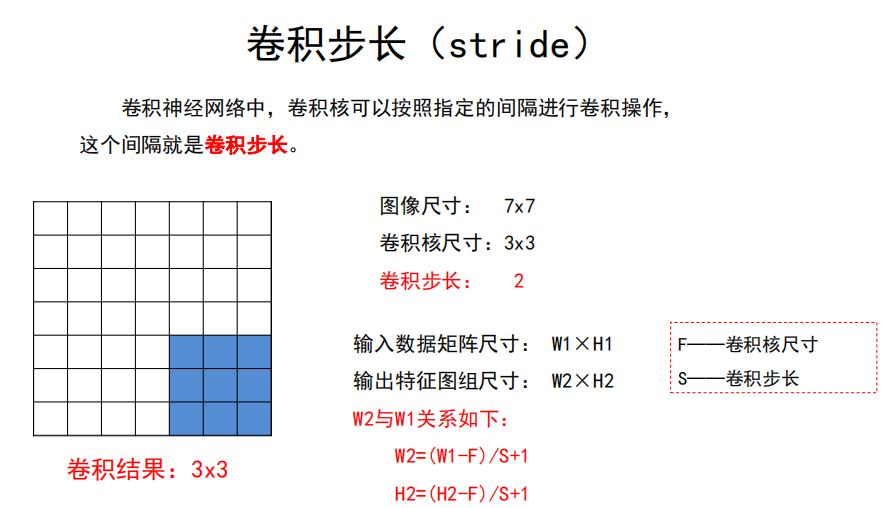
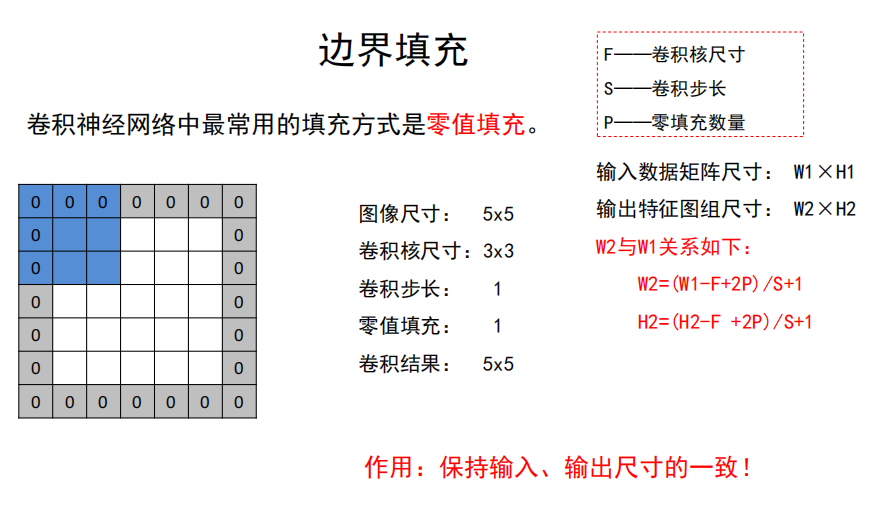
  • 步长与填充

    CN-E-3-1 CN-E-3-2

  • 输入输出公式

    W2=(W1−F+2P)/S+1H2=(H1−F+2P)/S+1D2=D1W_2 = (W_1 - F + 2P) / S+1 \\ H_2 = (H_1 - F +2P)/S +1 \\ D_2 = D_1

    因此，特征响应图组尺寸计算：

    CN-E-3-3

激活层 RELU

  • 与前面一样
    1. 比0小的：改为0
    2. 比0大的：本身

池化层 POOL

  • 池化的作用

    对每一个特征响应图独立进行，降低特征响应图组中每个特征响应图的宽度和高度，减少后续卷积层的参数的数量，降低计算资源耗费，进而控制过拟合。

    1. 降低计算量
    2. 扩大感受眼

    解释：因为每次池化会使得尺寸变小，是整体压缩变小，而当卷积核的大小只有那么大时，此时缩小了图，会使得卷积核能够感受到的范围，相对性地变大了！

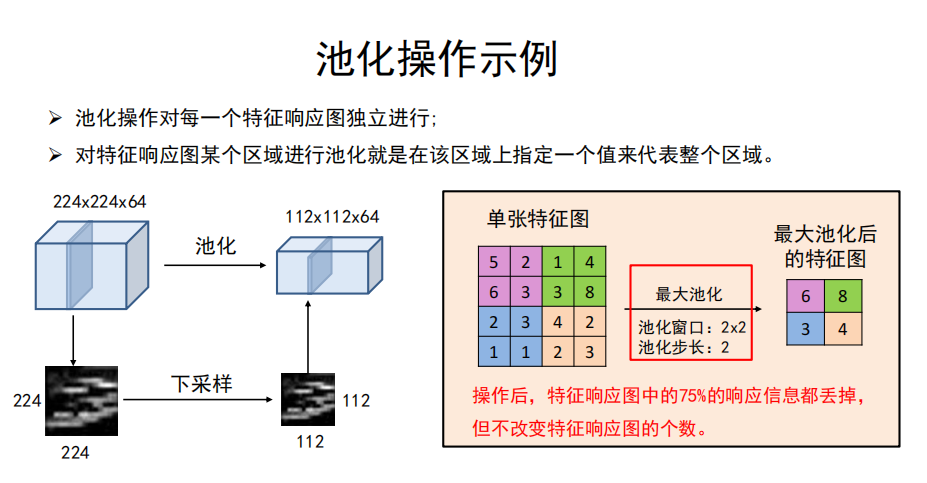
  • 池化操作

    对特征响应图某个区域进行池化就是在该区域上指定一个值来代表整个区域。

    • 常见的池化操作：

      • 最大池化——使用区域内的最大值来代表这个区域；
      • 平均池化——采用区域内所有值的均值作为代表。

    • 池化层的超参数

      • 池化窗口
      • 池化步长
    CN-E-3-4

全连接层 FC

  • 就是前面的全连接神经网络。

5.3 损失函数、优化算法

  • 损失函数
    • 交叉熵损失
  • 优化算法
    • SGD、带动量的SGD以及ADAM

5.4 样本增强

  • 存在的问题

    过拟合的原因是学习样本太少，导致无法训练出能够泛化到新数据的模型。

  • 数据增强

    是从现有的训练样本中生成更多的训练数据，其方法是利用多种能够生成可信图像的随机变换来增加样本。

  • 数据增强的目标

    模型在训练时不会两次查看完全相同的图像。

    这让模型能够观察到数据的更多内容，从而具有更好的泛化能力。

  • 各种方法

    • 翻转
    • 随机缩放、抠图
    • 色彩抖动
    • 随机联合下述操作
      1. 平移
      2. 旋转
      3. 拉伸
      4. 径向畸变（相关描述见摄像机几何章节）
      5. 裁剪

  • 示例

CN-E-4-1 CN-E-4-2 CN-E-4-3