GCN 图卷积神经网络

参考资料：

https://pyg.org/

https://networkx.org/

https://www.dgl.ai/

https://distill.pub/2021/gnn-intro/

https://distill.pub/2021/understanding-gnns/

参考视频：

https://www.bilibili.com/video/BV1Hs4y157Ls/

https://www.bilibili.com/video/BV1z14y1A7JX/

一、引入

假定我们有一个图 GG ：

  • VV 是节点集合vertex set
  • AA 是邻接矩阵Adjacency matrix 二进制
  • X∈R∣V∣×mX \in \mathbb{R}^{|V| \times m} 是节点特征矩阵

1. 原始想法

最初，我们当然是希望说，是否可以直接把整个 AA 和 XX 拼接起来，直接整个作为输入。

但是，实际上会有很多问题：

  1. 参数量过大
  2. 输入无法适应各种大小的图
  3. 对节点顺序敏感

我们知道，在 CNN 中，是用滑动窗口来实现各个区域的逐步卷积的。那是否可以使用 CNN 的滑动窗口思想？

也不行！因为图实际上根本不存在窗口的概念，一个图是可以拉伸变动节点的位置的，那你如何才能说某处是一个窗口呢？做不到。

好的，至此，我们归结出一些：

  • GNN 应该具有置换无关性Permutation Invariance，或说具有置换等价性Permutation Equivariant

注意，这一点是别的神经网络不具备的，卷积神经网络会有像素点位置信息，这些点的位置若是置换了就不对了；循环神经网络会有语序的先后，也是不能置换的。但是图神经网络，只要连接关系没有改变，是允许节点的位置置换摆动的。

2. GCN 思想

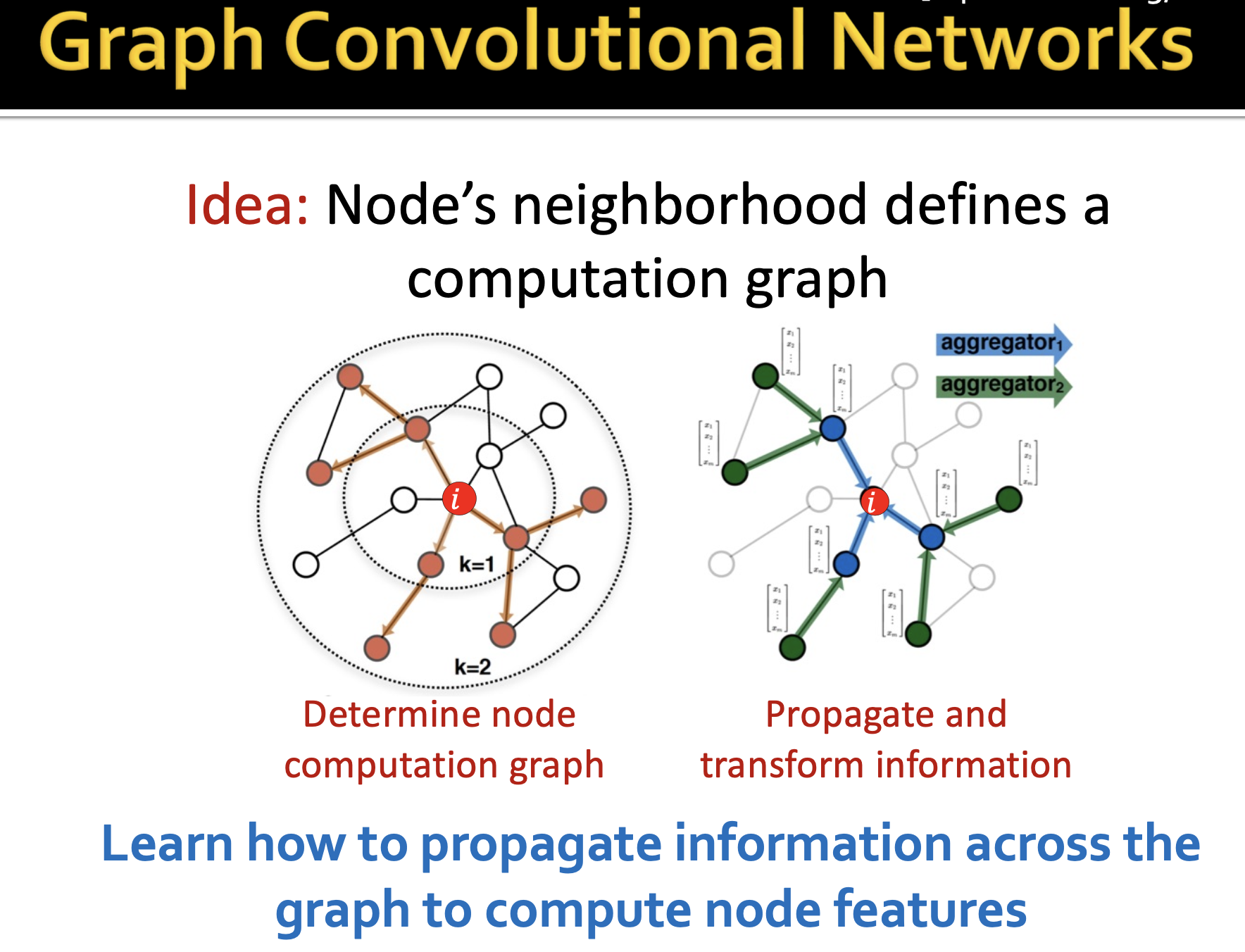
GCN思想

由此引出了 GCN 的思想，就是采用邻居节点来定义出计算图。如下图：

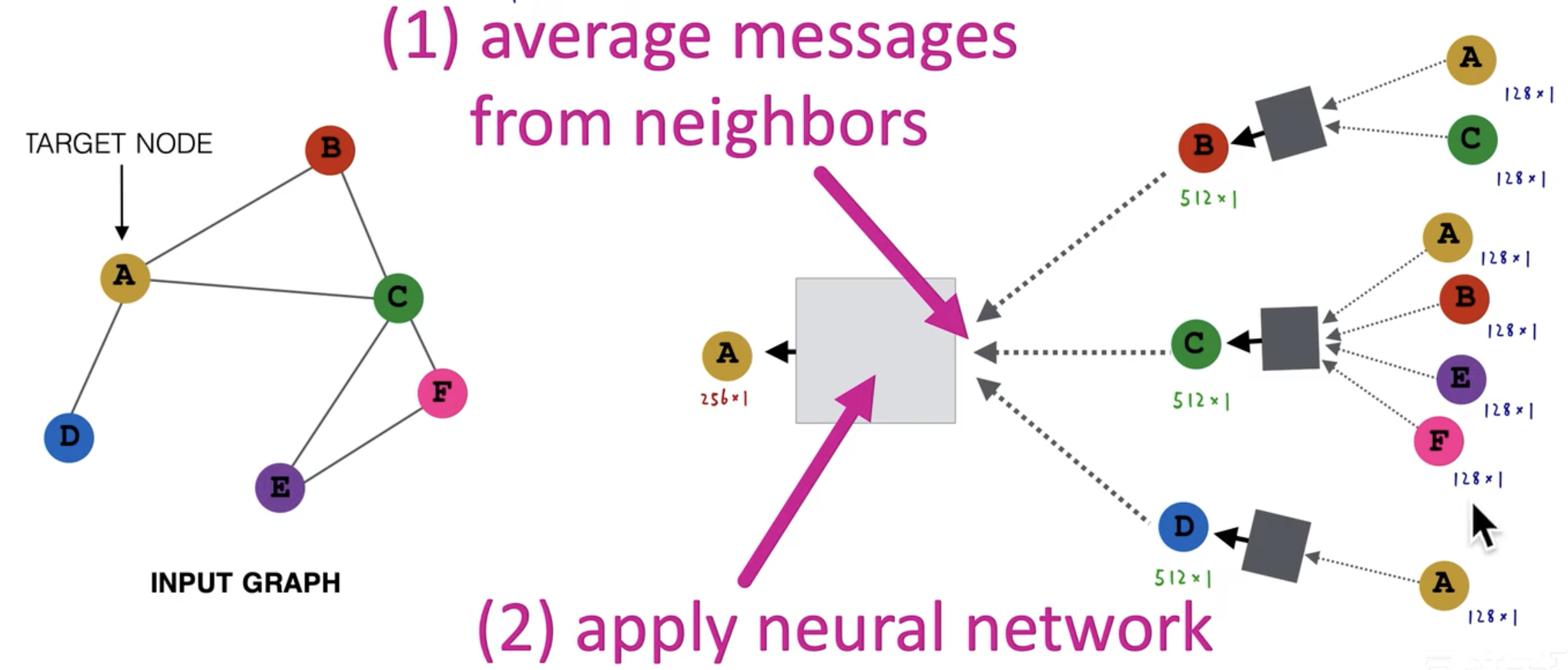
计算图思想

其中：

  1. 每个节点以自我为中心，将邻居节点传来的消息先进行取平均处理，然后作为本次的输入。
  2. 而邻居节点也有自己的邻居，他的来源可以是他的邻居节点向量。
  3. 每一层处理都是先聚合邻居传来的消息，在应用在神经网络的输入上。而这里神经网络就可以是各种各样的已有方法，因为到这里已经是序列化的向量了，对于向量输入的神经网络都能使用。
  4. 图神经网络的层数是取决于hops跳跃数。即，要深入查看几层邻居，上图是两层。
  5. 同一层神经网络（上图的灰色、黑色盒子）都是参数共享。
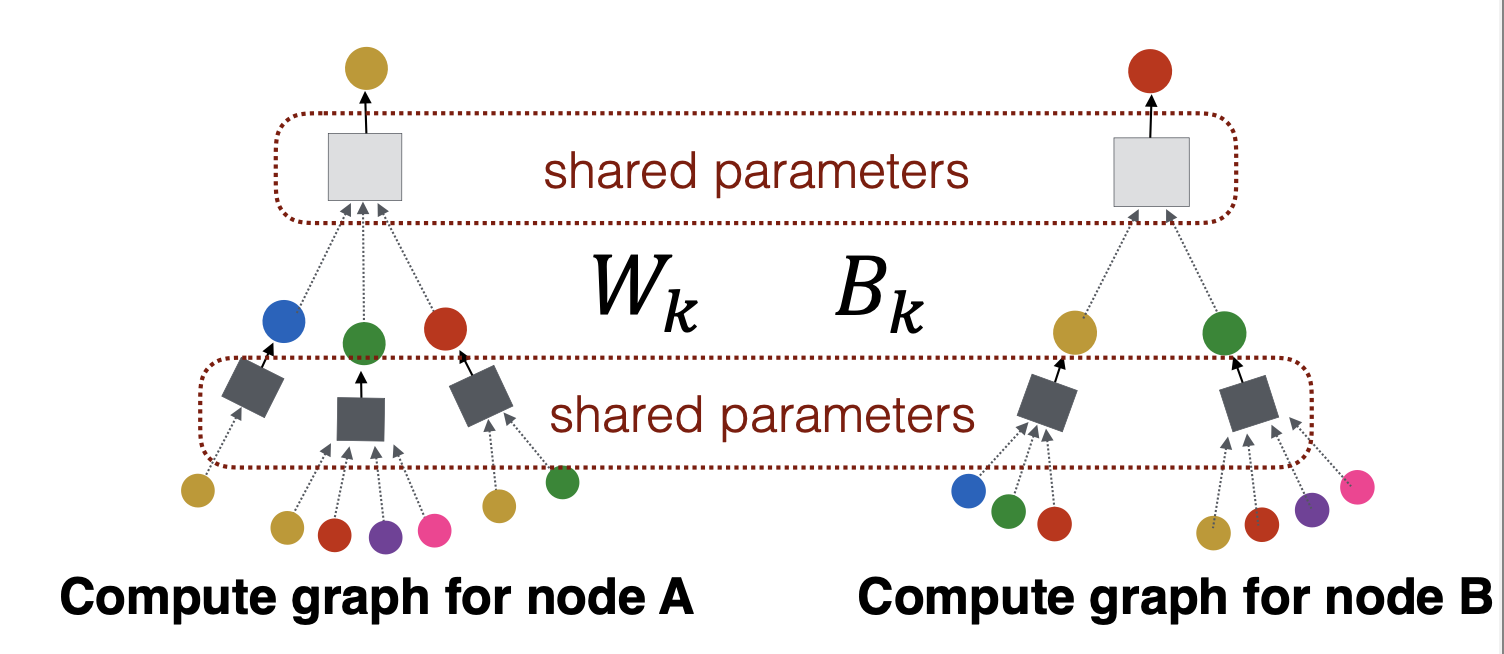
shared-parameters

注意：

  1. 每个节点的计算图会不一样吗？那这里也不具有大小适应性呀？

    的确每个节点的计算图会不同，但是具有大小适应性的。因为每一层盒子输入是取所有邻居节点向量的平均，所以说，盒子的输入向量维度是确定的。

  2. 计算图解决了什么问题？

    计算图充分利用了连接关系，同时具有置换等价性！计算图本身就是利用节点的连接关系构建出来的，这是天然的连接关系，同时因为是对所有邻居节点取平均，并不会因为输入的先后顺序而导致结果不同。

计算图

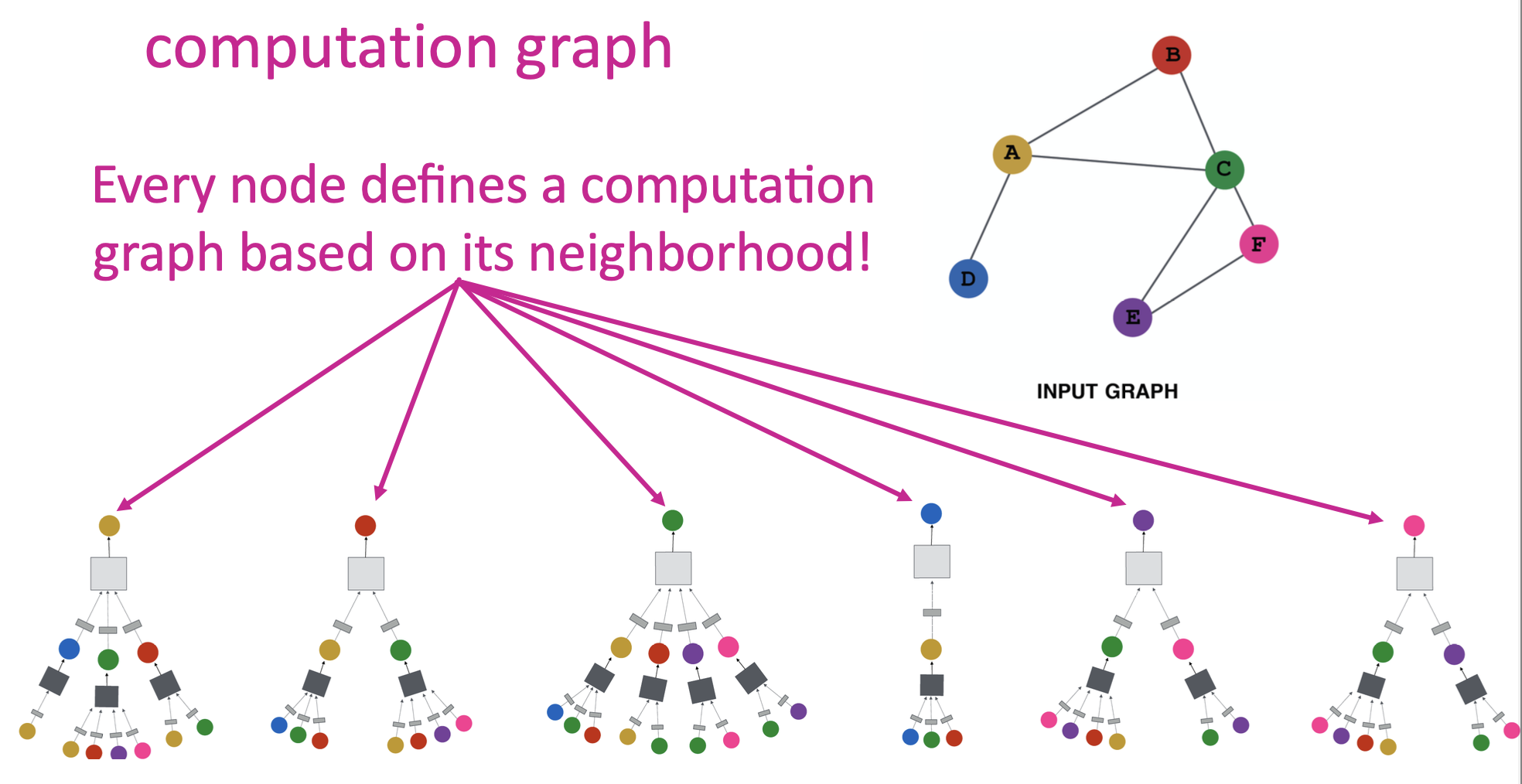
好的，至此，已经基本成型了。上面的计算图，我们看到每个节点都是由邻居节点来“评判”他自己，因此，可以完善一下，添加一个自我对自我的“评判”，就形成了完整的计算图：

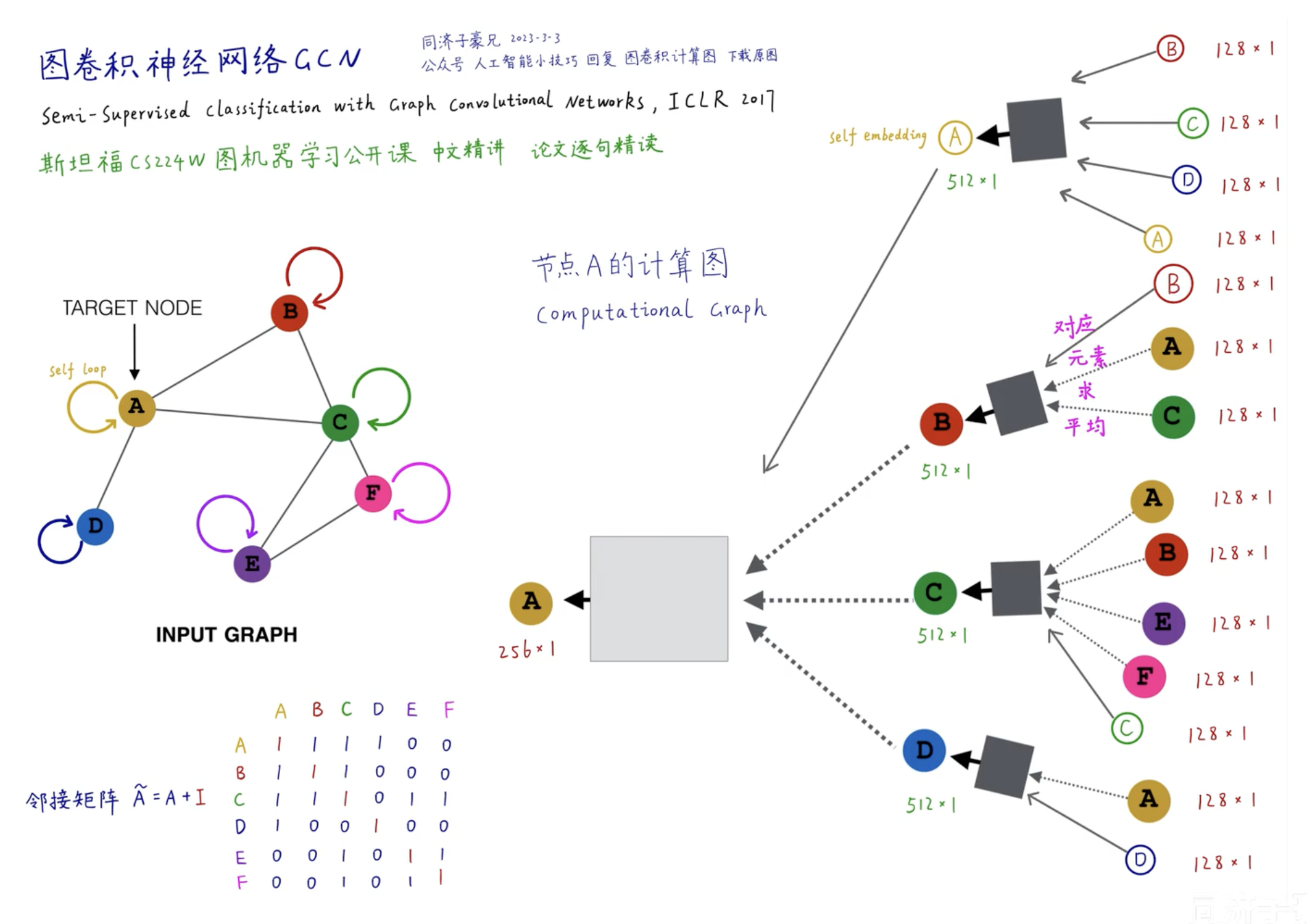
Full-Computation-Graph

二、GCN

1. 数学公式

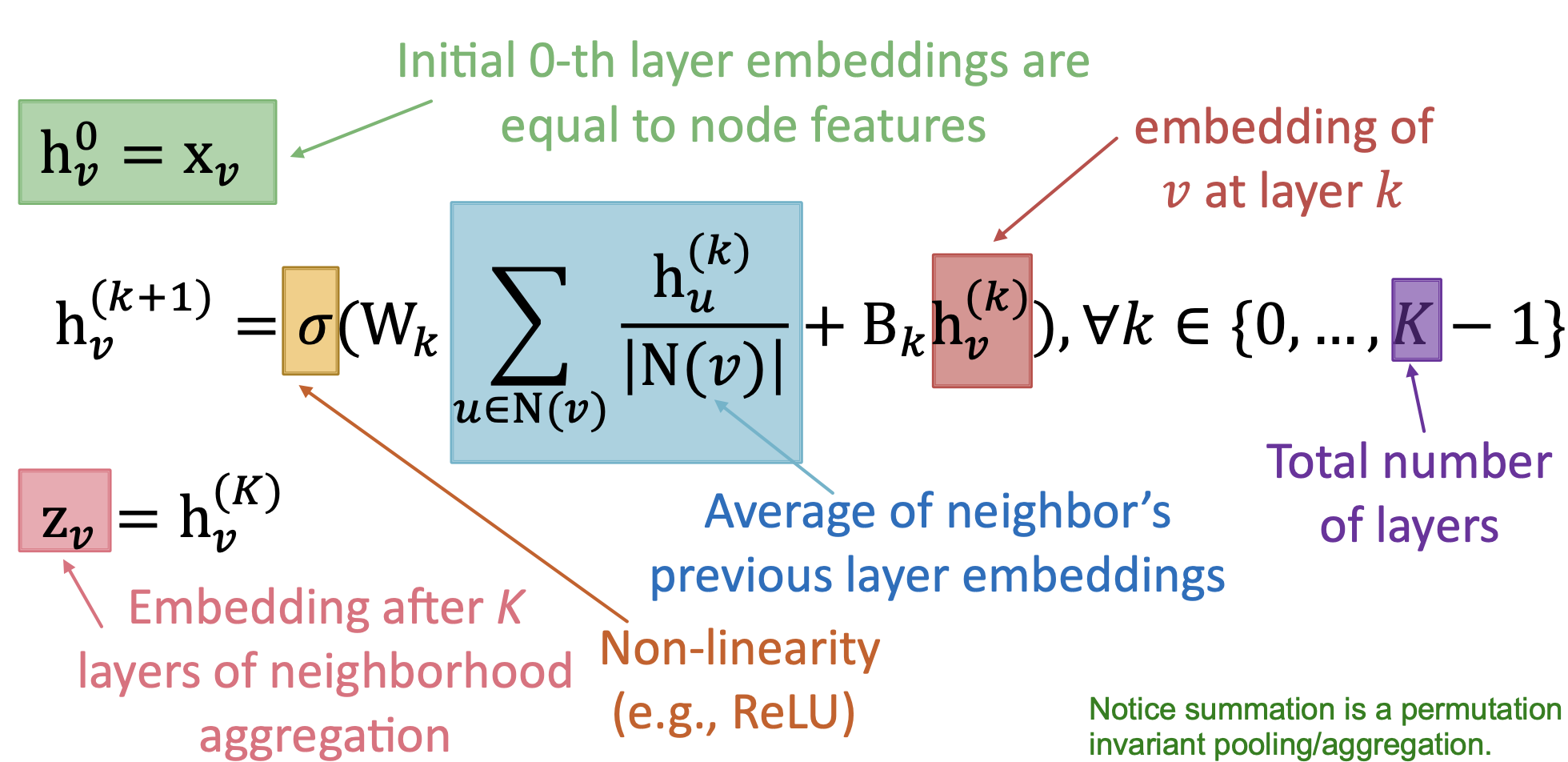
CG-Math

解释：

  1. 最初，第 0 层的输入 hv0h_v^0 就是节点的原始特征向量。
  2. 后一层 hvk+1h_v^{k+1} 是由前一层输入 hvkh_v^{k} 得来，具体操作是：
    • 先对每个邻居节点的输入 hukh_u^{k} 按照邻居的度作为均摊权重来进行消息传递
    • 自身在本层的向量 hvkh_v^{k} 也会有消息传递
    • 上述两种消息的处理会不同，一个是左乘参数 WkW_k ，一个是左乘 BkB_k
    • 然后输入给非线性函数 σ\sigma ，就得到输出 hvk+1h_v^{k+1}
  3. 最终的输出，就是最后一层的向量 hvKh_v^{K}

  1. 为什么使用邻居的度作为均摊权重？

    因为这样做，可以使得度越少的节点对外影响更大，而一个度很多的节点可能是很泛滥的，那么他对其他节点的影响大概率是不那么重要的，那么按照度来均摊，他的确无法造成太大影响。这样做符合现实要求。

  2. 前后层的向量维度需要一样吗？

    不需要，这里就是让你设计输入输出维度了，和非图结构的神经网络一样的设计思想。

  3. 最终的输出有什么意义？

    最终输入就是 Node Embedding ！这就完成了图嵌入问题，这与以往的方法不同，我们这里是可以使用机器学习的方法（MLP）来完成训练，让其自动学到参数 Wk、BkW_k 、 B_k 的值。而学习完成后就能实现对任何一个输入节点都能自动得到这个节点的节点向量了。这称为归纳式学习。

  4. 那么最终输出有什么要求吗？

    低维、连续、稠密。

    • 低维：相对于节点原始特征向量而言，更低维度，否则为什么不直接把原始特征向量作为 Node Embedding。
    • 连续：每个节点都是实数的，有正有负，有大有小。
    • 稠密：向量的元素都不为 0。

可以把公式以矩阵的形式写得更加简洁：

Math

2. 训练

训练思想有两种：

  1. 无监督学习
  2. 监督学习

各自应用于不同的任务，损失函数定义不同。

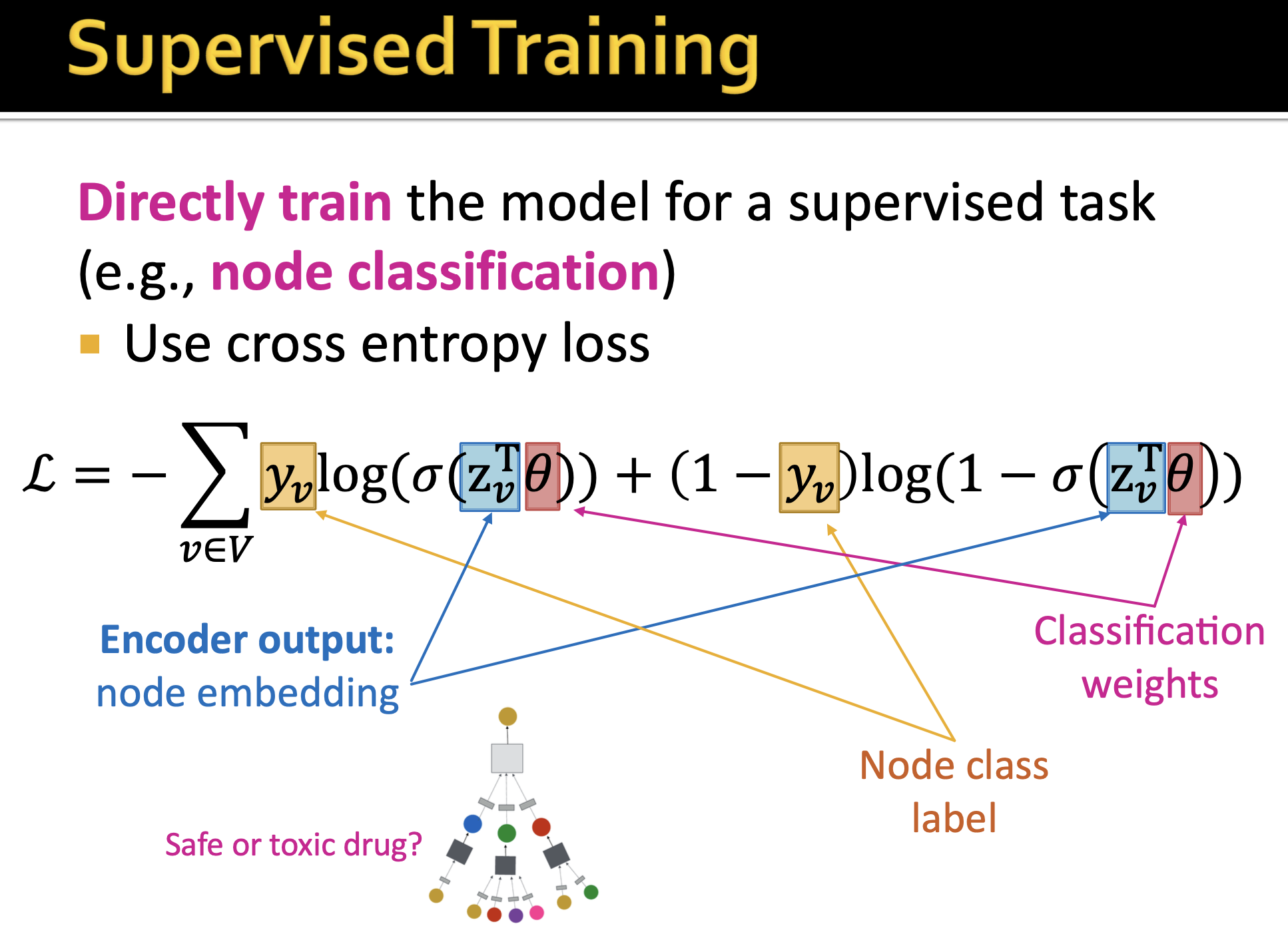
Unsupervised Supervised

三、表达能力

1. 节点的区分性

实际上，GNN 的表达能力，就等于是，区分计算图根节点Embedding 的能力

理想的 GNN 应该是，对于不同的计算图根节点，输出不同的 Embedding。

按照这个思想，可以看到，节点 1 和节点 2 是无法区分的，或者说，他们俩本身就是很相似，他们应该得到差不多的 Embedding。而对于节点 3/4/5 会被区分开来，他们的计算图都不一样，自然 Embedding 会大不相同。

解释性

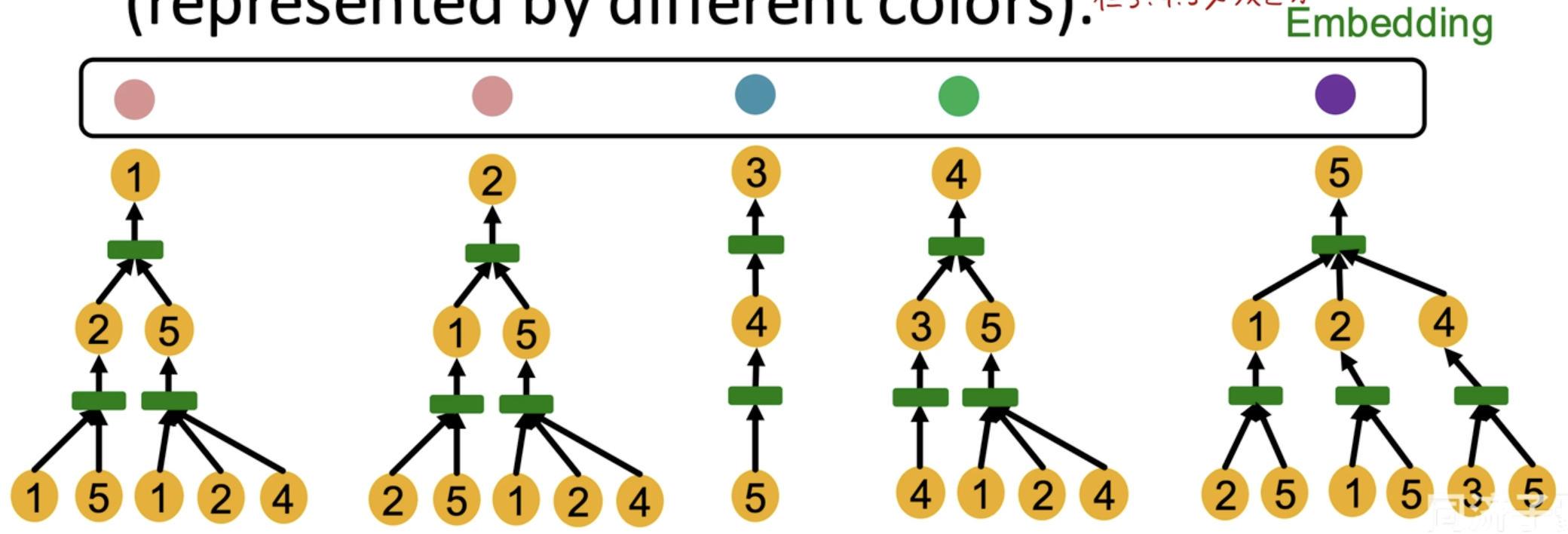
注意：我们知道如若对于上一层的消息传递，只是简单的取平均的话，那么区分性实际上大打折扣，所以说，我们可以采用更多的单射函数操作，来保证区分性（本质上，也是一种 HASH）

2. 联想 Weisfeiler-Lehman Kernel 算法

WL 算法是传统的特征提取方法，很复杂，不是重点，具体示例如下图：

WL-1 WL-2

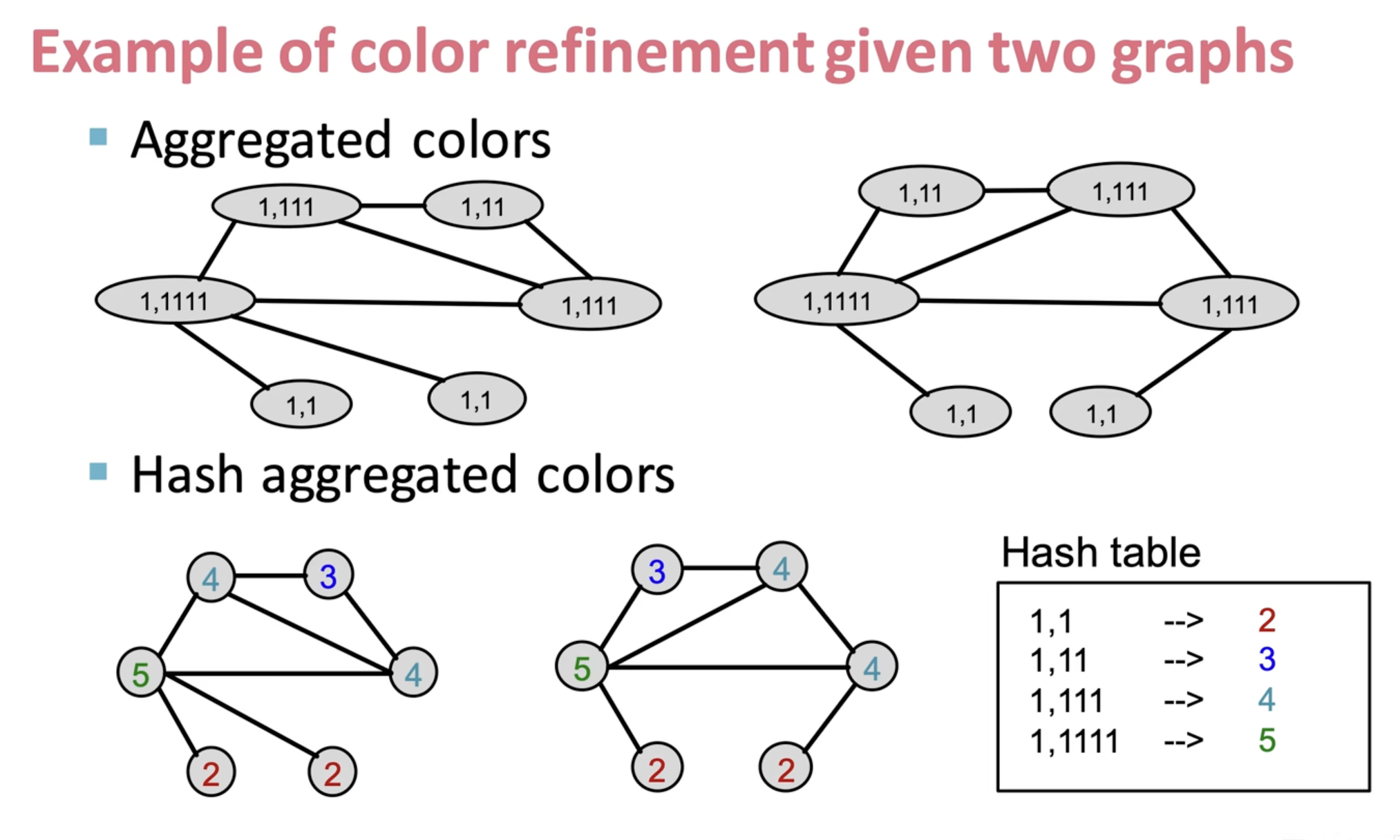
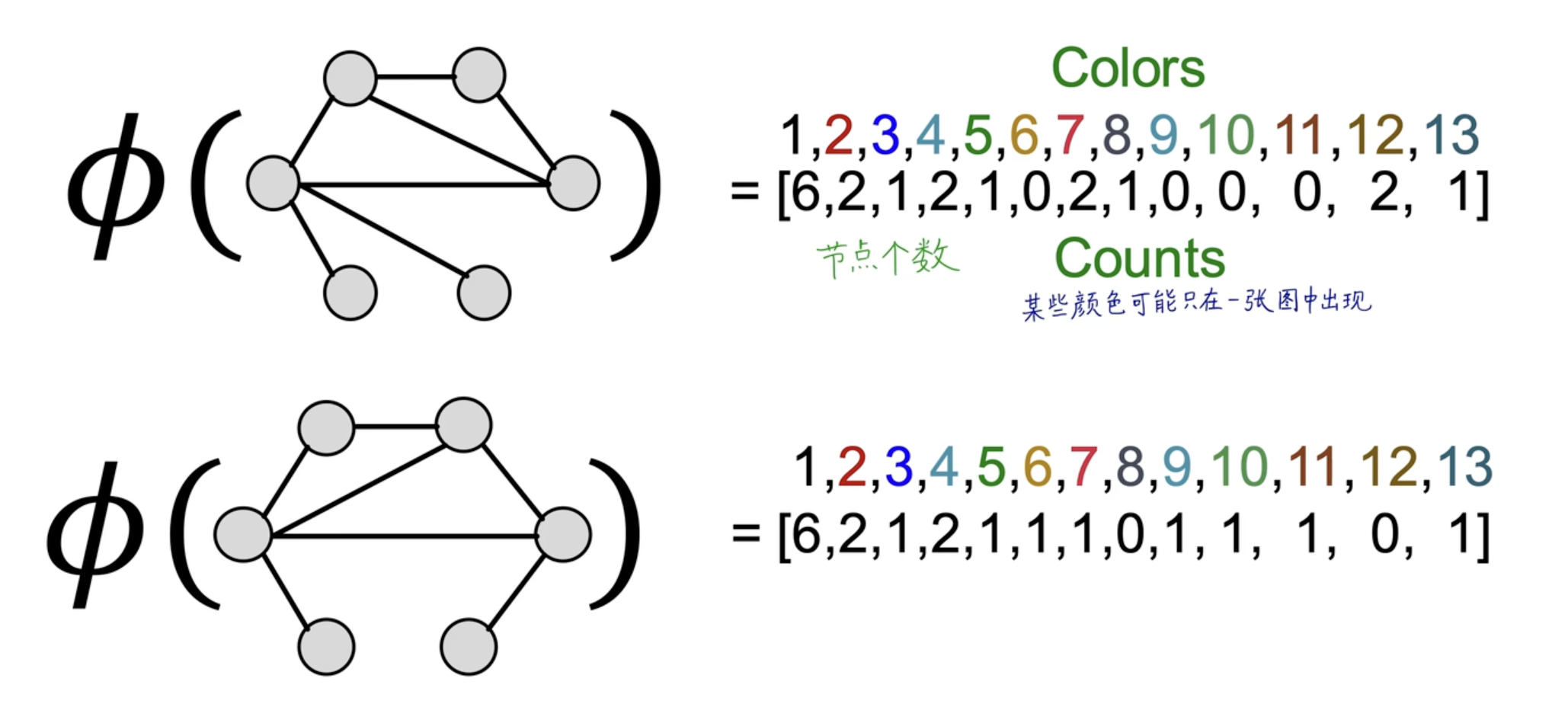
但是，这个操作无法简单泛化，但很精确。它是 GCN 计算图的性能上界。

再思考，你会发现，本质上，计算图的构建似乎也和 WL 算法很相似。

四、完整推导

1. 完整公式

按照原作者论文SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS 的数学公式如下：

H(l+1)=σ(D~−12A~D~12H(l)W(l))H^{(l+1)} = \sigma \big( \widetilde{D}^{-\frac{1}{2}} \widetilde{A} \widetilde{D}^{\frac{1}{2}} H^{(l)} W^{(l)} \big)

说明：

  • σ\sigma 是激活函数
  • DD 是度矩阵，D~=D+I\widetilde{D} = D + I
  • AA 是邻接矩阵，A~=A+I\widetilde{A} = A +I
  • H(l)H^{(l)} 是第 ll 层输入输出
  • W(l)W^{(l)} 是第 ll 层训练参数

2. 推导理解

以下面的图为例：

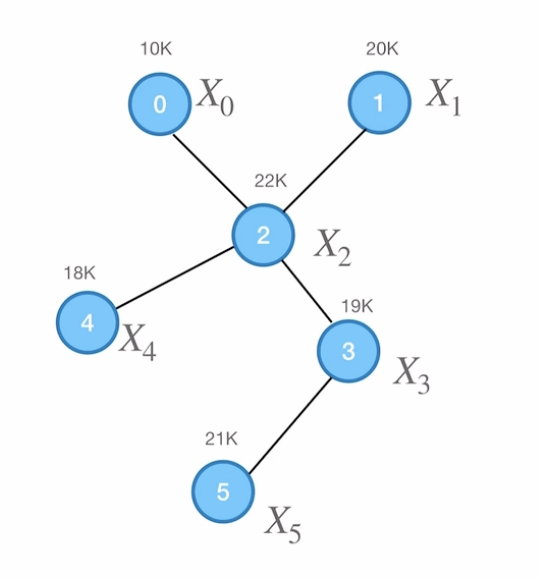
Example

融合信息

邻接矩阵AA 和属性矩阵XX 分别是：

A=[001000001000110110001001001000000100]X=[X0X1X2X3X4X5]=[102022191821]A = \begin{bmatrix} 0&0&1&0&0&0\\ 0&0&1&0&0&0\\ 1&1&0&1&1&0\\ 0&0&1&0&0&1\\ 0&0&1&0&0&0\\ 0&0&0&1&0&0\\ \end{bmatrix} \quad \quad X = \begin{bmatrix} X_0\\ X_1\\ X_2\\ X_3\\ X_4\\ X_5\\ \end{bmatrix} = \begin{bmatrix} 10\\ 20\\ 22\\ 19\\ 18\\ 21\\ \end{bmatrix}

下面看，如果是融合邻居节点属性信息来更新 2 号节点的值：

aggregate(X2)=X0+X1+X3+X4=1⋅X0+1⋅X1+0⋅X2+1⋅X3+1⋅X4+0⋅X5=∑j=0NA2jXj=A2Xaggregate(X_2) = X_0 + X_1 + X_3 + X_4 \\ = 1 \cdot X_0 + 1 \cdot X_1 + 0 \cdot X_2 + 1\cdot X_3 +1 \cdot X_4 + 0 \cdot X_5 \\ = \sum_{j=0}^{N}{A_{2j}X_j} \\ = A_2 X

那么，实际上，对于每一个节点的融合，可以统一在一个矩阵里面：

aggregate(X)=aggregate([X0X1X2X3X4X5])=[A0XA1XA2XA3XA4XA5X]=AXaggregate(X) = aggregate( \begin{bmatrix} X_0\\ X_1\\ X_2\\ X_3\\ X_4\\ X_5\\ \end{bmatrix} )= \begin{bmatrix} A_0 X\\ A_1 X\\ A_2 X\\ A_3 X\\ A_4 X\\ A_5 X\\ \end{bmatrix} = AX

然而，上面我们融合信息时，都没有考虑自己的信息，所以下面把自身节点的信息也融合进去考虑：

例如，对于 2 号节点，就是把 aggregate(X2)aggregate(X_2) 中的 0⋅X20\cdot X_2 改成 1⋅X21\cdot X_2即可，那么我们可以定义出：

A~=A+I=[101000011000111110001101001010000101]\widetilde{A} = A + I = \begin{bmatrix} 1&0&1&0&0&0\\ 0&1&1&0&0&0\\ 1&1&1&1&1&0\\ 0&0&1&1&0&1\\ 0&0&1&0&1&0\\ 0&0&0&1&0&1\\ \end{bmatrix}

由此，公式就是 aggregate(X)=A~Xaggregate(X) = \widetilde{A}X。

权重平均

然而，我们不能直接加起来就结束了，因为每次融合信息是直接输入到 NN 里的，那我们应该保证这个输入是具有普遍意义的。按照直接相加的话，节点越多，那融合结果就越大了，这不太符合现实意义。

换言之，应该按照相加的节点数，来取平均，才更有参考意义。2 号节点是0、1、2、3、4节点融合而来，一共是五个节点，因此除以 5，那 5 其实就是 2 号节点的度数，引出度数矩阵DD ：

D=[100000010000004000000200000010000001]D~=D+I=[200000020000005000000300000020000002]D = \begin{bmatrix} 1&0&0&0&0&0\\ 0&1&0&0&0&0\\ 0&0&4&0&0&0\\ 0&0&0&2&0&0\\ 0&0&0&0&1&0\\ 0&0&0&0&0&1\\ \end{bmatrix} \quad \quad \widetilde{D} = D+I = \begin{bmatrix} 2&0&0&0&0&0\\ 0&2&0&0&0&0\\ 0&0&5&0&0&0\\ 0&0&0&3&0&0\\ 0&0&0&0&2&0\\ 0&0&0&0&0&2\\ \end{bmatrix}

下面对于融合：

aggregate(X2)=∑j=0NA2jXj5=∑j=0NA2jXjD~22aggregate(X_2) = \sum_{j=0}^{N}{\frac{A_{2j}X_j}{5}} = \sum_{j=0}^{N}{\frac{A_{2j}X_j}{\widetilde{D}_{22}}}

双向考虑

我们上述是考虑自己节点的度数来作为分母权重，而如若是考虑边双方节点的度数是否更具有参考意义，同时为了保持分母是一次，我们采用开根号，再考虑：

A~32X2D~33+A~33X3D~33+A~34X4D~33=A~32X2D~33D~33+A~33X3D~33D~33+A~34X4D~33D~33\frac{\widetilde{A}_{32}X_2}{\widetilde{D}_{33}} + \frac{\widetilde{A}_{33}X_3}{\widetilde{D}_{33}} + \frac{\widetilde{A}_{34}X_4}{\widetilde{D}_{33}}\\ = \frac{\widetilde{A}_{32}X_2}{\sqrt{\widetilde{D}_{33}\widetilde{D}_{33}}} + \frac{\widetilde{A}_{33}X_3}{\sqrt{\widetilde{D}_{33}\widetilde{D}_{33}}} + \frac{\widetilde{A}_{34}X_4}{\sqrt{\widetilde{D}_{33}\widetilde{D}_{33}}}\\

好的，那我们可以把分母改一改，考虑边的双方节点度数：

A~32X2D~33D~22+A~33X3D~33D~33+A~34X4D~33D~44\frac{\widetilde{A}_{32}X_2}{\sqrt{\widetilde{D}_{33}\widetilde{D}_{22}}} + \frac{\widetilde{A}_{33}X_3}{\sqrt{\widetilde{D}_{33}\widetilde{D}_{33}}} + \frac{\widetilde{A}_{34}X_4}{\sqrt{\widetilde{D}_{33}\widetilde{D}_{44}}}

统一一下，即：

aggregate(Xi)=∑j=0NA~ijXjD~iiD~jjaggregate(X_i) = \sum_{j=0}^N{\frac{\widetilde{A}_{ij}X_j}{\sqrt{\widetilde{D}_{ii}\widetilde{D}_{jj}}}}

3. 最终公式

现在，可以全部整理一下：

aggregate(X)=∑i=0Naggregate(Xi)=∑i=0N∑j=0NA~ijXjD~iiD~jj=∑i=0N∑j=0ND~ii−12A~ijD~jj−12Xj=∑i=0ND~ii−12A~iD~−12X=D~−12A~D~−12Xaggregate(X) = \sum_{i=0}^{N}{aggregate(X_i)} = \sum_{i=0}^{N}{\sum_{j=0}^N{\frac{\widetilde{A}_{ij}X_j}{\sqrt{\widetilde{D}_{ii}\widetilde{D}_{jj}}}}} \\ = \sum_{i=0}^{N}{\sum_{j=0}^N{ \widetilde{D}_{ii}^{-\frac{1}{2}} \widetilde{A}_{ij} \widetilde{D}_{jj}^{-\frac{1}{2}} X_j}} \\ = \sum_{i=0}^{N}{ \widetilde{D}_{ii}^{-\frac{1}{2}} \widetilde{A}_{i} \widetilde{D}^{-\frac{1}{2}} X} \\ = \widetilde{D}^{-\frac{1}{2}} \widetilde{A} \widetilde{D}^{-\frac{1}{2}} X

右乘训练参数，再激活，就是输出：

H=σ(aggregate(X)W)=σ(D~−12A~D~−12XW)H = \sigma \Big( aggregate(X) W \Big) \\ =\sigma \Big( \widetilde{D}^{-\frac{1}{2}} \widetilde{A} \widetilde{D}^{-\frac{1}{2}} X W \Big)

即，融合邻居的信息得到 aggregate(H(l))aggregate(H^{(l)}) ，然后乘以训练参数W(l)W^{(l)}，再使用 σ\sigma 激活，就是得到输出 H(l+1)H^{(l+1)} 。

然后多层操作，下一层的输入 XX 就是上一层的输出 HH ，每层的参数 WW 不同，就得到了论文的公式：

H(l+1)=σ(D~−12A~D~12H(l)W(l))其中，H(0)=XH^{(l+1)} = \sigma \big( \widetilde{D}^{-\frac{1}{2}} \widetilde{A} \widetilde{D}^{\frac{1}{2}} H^{(l)} W^{(l)} \big) \\ 其中，H^{(0)} = X

以上就是全部推导理解。