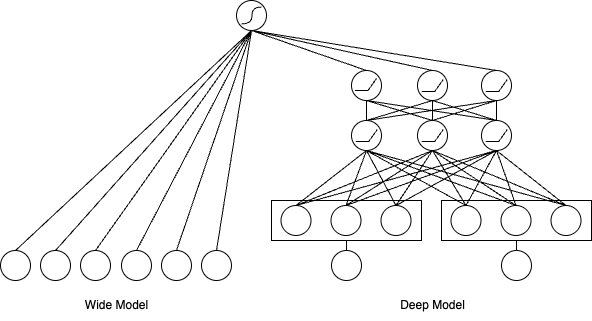
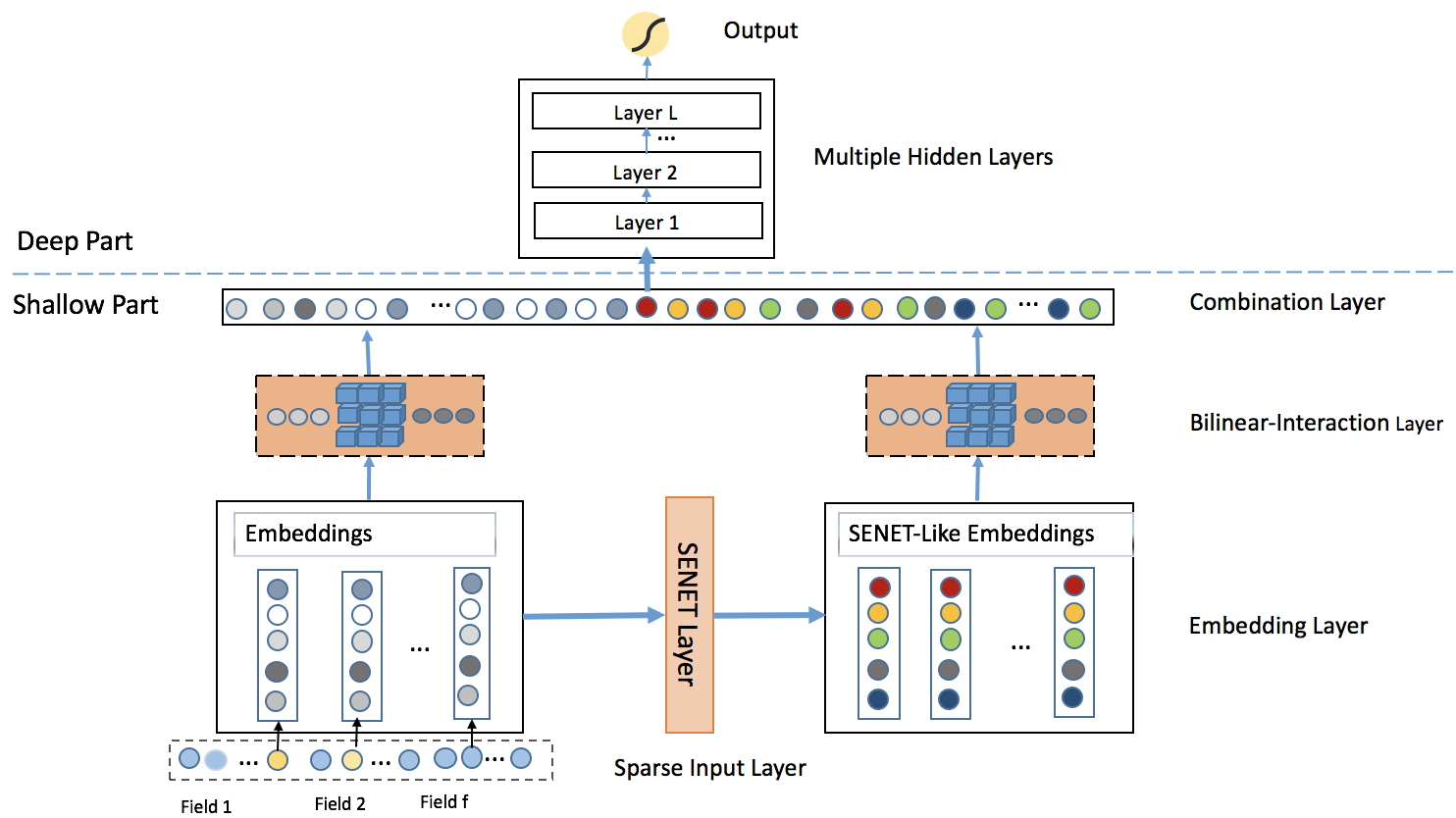
参考

精排（四）多目标建模

多目标建模（Multi-Task Learning, MTL）通过联合优化多个相关任务，在推荐系统中实现用户体验与商业目标的协同提升。相比独立建模，多目标方法能够降低参数量、提升系统效率，并通过知识迁移缓解数据稀疏问题。

在实际应用中，电商场景联合优化CTR、CVR、GMV避免单一指标导致的低质商品推荐；视频平台同时优化播放完成率、评分预测、用户留存率提升长期用户价值。然而，多目标建模面临任务冲突、跷跷板效应和负迁移等核心挑战。

针对这些挑战，业界发展出三大解决方向：模型架构从Shared-Bottom到MMoE再到PLE的演进，解决任务冲突与负迁移；ESMM和ESM2等依赖关系建模方法，处理用户行为链路的样本偏差；以及从手工加权到自适应优化的多损失融合策略，解决量级失衡与收敛异步问题。

本章将详细介绍这些核心技术的原理与实践。

1、基础结构演进

1.1 Shared-Bottom

原理

Shared-Bottom 模型作为多目标建模的奠基性架构，采用"共享地基+独立塔楼"的设计范式。其核心结构包含两个关键组件：

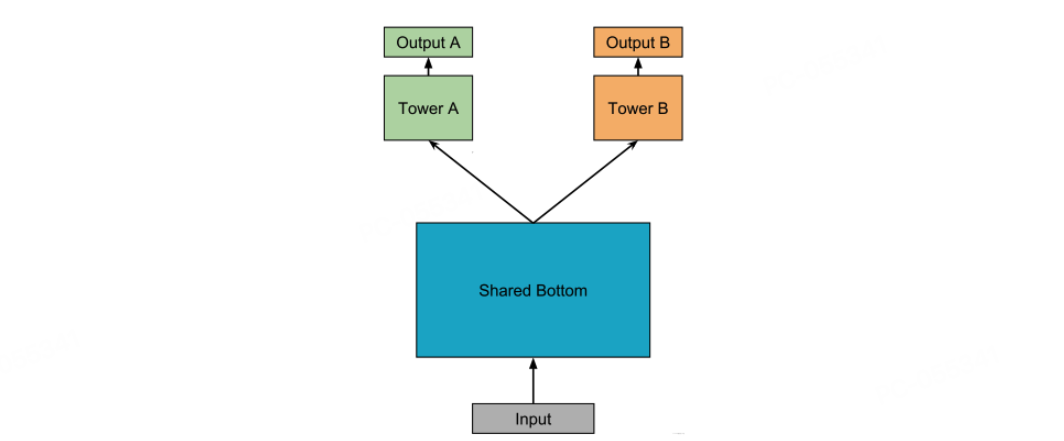
共享底层（Shared Bottom）：所有任务共用同一组特征转换层，负责学习跨任务的通用特征表示；
任务特定塔（Task-Specific Towers）：每个任务拥有独立的顶层网络，基于共享表示学习任务特定决策边界。

Shared-Bottom

这种架构的数学表达可描述为：

$\hat{y}_t = f_t(W_t \cdot g(W_s \mathbf{x}))$

其中 $\mathbf{W}_s$ 为共享层参数， $g(\cdot)$ 为共享特征提取函数， $f_t(\cdot)$ 为任务 $t$ 的预测函数。其设计哲学建立在任务同质性假设上：不同任务共享相同的底层特征空间，仅需在顶层进行任务适配。

Shared-Bottom 模型在效率与泛化之间实现了良好的平衡，其核心优势主要体现在以下几点。

在参数效率方面，共享层占据了模型大部分的参数量这显著降低了模型的总参数量。
共享层具有正则化效应，它如同一个天然的正则化器，通过强制任务共用特征表示，有效防止了单个任务出现过拟合的情况。
在知识迁移方面，当任务之间存在潜在的相关性时，例如视频的点击率与完播率，共享层能够学习到通用的模式，从而提升小样本任务的泛化能力。

然而，Shared-Bottom 模型也存在一个致命缺陷，即负迁移现象。当任务之间存在本质上的冲突时，该模型的硬共享机制会引发负迁移问题。从机制本质上来看，共享层的梯度更新方向是由所有任务共同决定的，一旦任务目标之间出现冲突，参数优化就会陷入方向性的矛盾。

在一些典型场景中，例如电商平台同时优化“点击率”与“客单价”时，低价商品可能会推动点击率的提升，但同时却抑制了客单价的增长；又如内容平台在平衡“内容消费深度”与“广告曝光量”时，深度阅读行为往往与广告点击行为呈负相关。

从数学角度来解释，假设任务 $i$ 与任务 $j$ 的损失梯度分别为 $\nabla L_i$ 与 $\nabla L_j$ ，当 $\nabla L_i \cdot \nabla L_j$ < 0时，共享层参数更新就会产生内在的冲突。这种冲突使得模型在处理矛盾任务时呈现出“零和博弈”的特性，即提升某一目标的性能往往需要以牺牲另一目标为代价，我们一般也称这类问题为跷跷板问题。

代码

shared-bottom模型构建代码如下，先组装输入到shared-bottom网络中的特征dnn_inputs, 经过一个shared-bottom DNN网络，遍历创建各个任务独立的DNN塔，最后输出多个塔的预估值用于计算Loss。
shared_bottom.py 文件：

import tensorflow as tf

from .utils import (
    build_input_layer,
    build_group_feature_embedding_table_dict,
    concat_group_embedding,
)
from .layers import DNNs, PredictLayer


def build_shared_bottom_model(feature_columns, model_config):
    """
    构建Shared-Bottom多任务排序模型。

    Args:
        feature_columns: FeatureColumn列表
        model_config: 包含参数的字典:
            - task_names: 列表，任务名称 (默认 ["is_click"])
            - share_dnn_units: 列表，共享底层DNN隐藏单元 (默认 [128, 64])
            - task_tower_dnn_units: 列表，任务塔DNN隐藏单元 (默认 [128, 64])
            - dropout_rate: 浮点数，dropout率 (默认 0.1)

    Returns:
        (model, None, None): 排序模型元组
    """
    task_names = model_config.get("task_names", ["is_click"])
    share_dnn_units = model_config.get("share_dnn_units", [128, 64])
    task_tower_dnn_units = model_config.get("task_tower_dnn_units", [128, 64])
    dropout_rate = model_config.get("dropout_rate", 0.1)

    # 输入层
    input_layer_dict = build_input_layer(feature_columns)

    # 分组嵌入
    group_embedding_feature_dict = build_group_feature_embedding_table_dict(
        feature_columns, input_layer_dict, prefix="embedding/"
    )

    # 连接不同组的嵌入向量作为网络的输入
    dnn_inputs = concat_group_embedding(group_embedding_feature_dict, "shared_bottom")

    # 构建共享底层DNN层
    shared_bottom_feature = DNNs(
        name="shared_bottom", units=share_dnn_units, dropout_rate=dropout_rate
    )(dnn_inputs)

    # 构建任务特定塔
    task_output_list = []
    for task_name in task_names:
        task_output_logit = DNNs(
            name=f"task_tower_{task_name}",
            units=task_tower_dnn_units + [1],
            dropout_rate=dropout_rate,
        )(shared_bottom_feature)

        task_output_prob = PredictLayer(name=f"task_{task_name}")(task_output_logit)
        task_output_list.append(task_output_prob)

    # 构建模型，输出任务输出列表
    model = tf.keras.models.Model(
        inputs=list(input_layer_dict.values()), outputs=task_output_list
    )
    return model, None, None

1.2 MMOE

原理

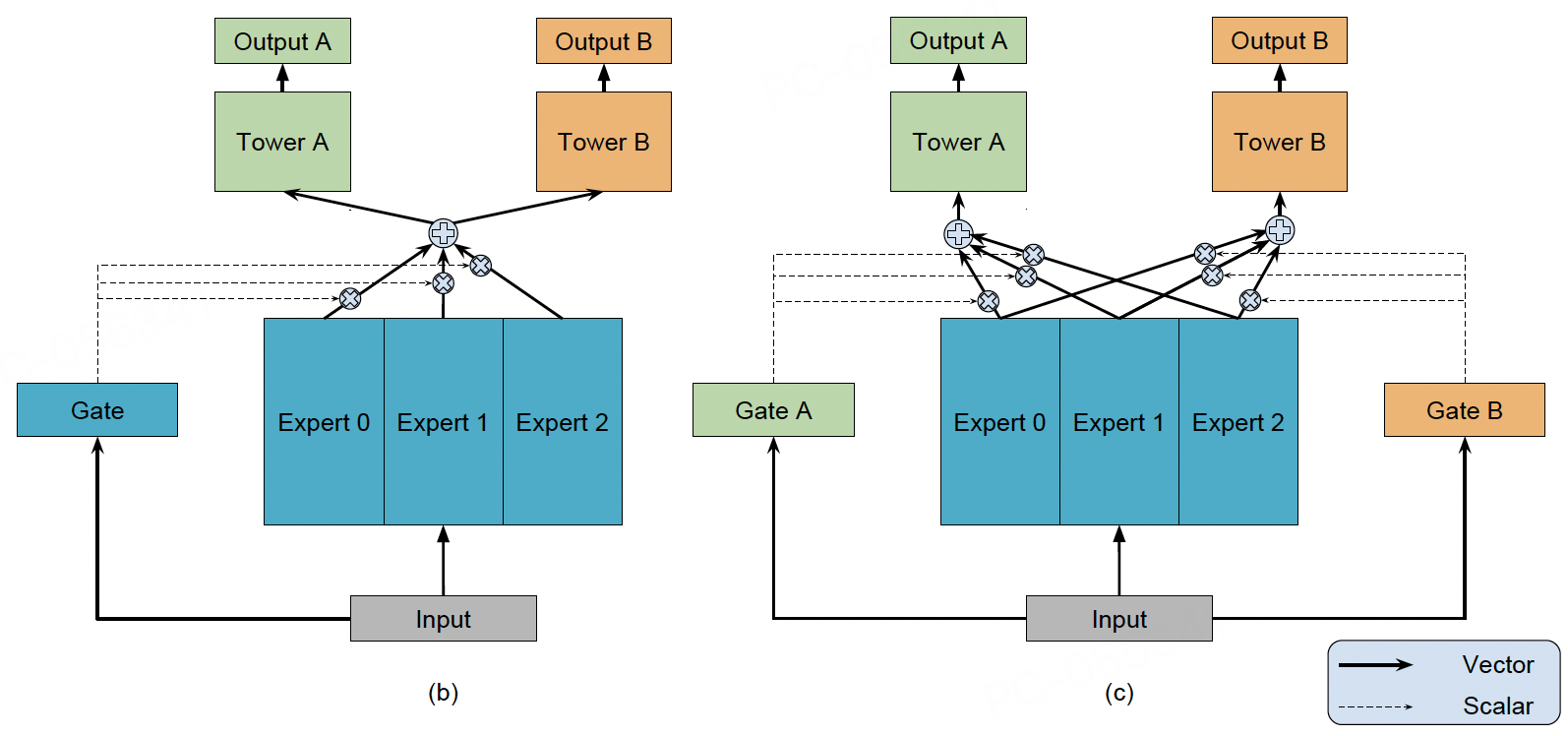
MMOE模型结构

针对Shared-Bottom对相关性低的多个任务出现负迁移的现象，OMOE将底层共享的一个Shared-Bottom模块拆分成了多个Expert，最终OMOE的输出为多个Expert的加权和，本质可以看成是专家网络和全局门控的双层结构。

虽然OMOE通过底层多专家融合的方式提升了特征表征的多样性，从最终的实验结果看，确实可以一定程度上缓解低相关性任务的负迁移问题，但没有彻底解决多任务冲突的问题。因为不同任务反向传播的梯度还是会直接影响底层专家网络的学习。

为了进一步缓解多任务冲突，MMOE为每个任务配备专属门控网络，实现了门控从"全局共享"升级为"任务自适应"的方式。MMoE的数学表达式可以表示为：

$\begin{aligned} \mathbf{e}_k &= f_k(\mathbf{x}) \\ g_t(\mathbf{x}) &= \text{softmax}(\mathbf{W}_t \mathbf{x}) \\ \mathbf{h}_t &= \sum_{k=1}^K g_{t,k} \cdot \mathbf{e}_k \\ \hat{y}_t &= f_t(\mathbf{h}_t) \end{aligned}$

其中，

$\mathbf{x}$ 表示底层的特征输入
$\mathbf{e}_k$ 表示第k个专家网络的输出
$g_t(\mathbf{x})$ 表示第 $t$ 个任务融合专家网络的门控向量
$\mathbf{h}_t$ 表示第 $t$ 个任务融合专家网络的输出
$\hat{y}_t$ 表示第 $t$ 个任务的预测结果

差异化特征融合门控网络 $g_t$ 根据任务特性选择专家组合，例如在电商场景，CTR任务门控加权"即时兴趣"“价格敏感"专家，CVR任务门控：侧重"消费能力”"品牌忠诚"专家。

当任务 $i$ 与 $j$ 冲突时，如果模型学的还不错，那么这两个任务对所有Expert的融合权重是有差异的。例如出现了某个 $e_m$ 专家，对于任务 $i$ 来说非常大，但是对于任务 $j$ 来说非常小，那么最终 $e_m$ 参数的更新就会被任务 $i$ 来主导，起到了一定的梯度隔离的效果。

代码

MMoE模型构建代码如下，先组装输入到MoE网络中的特征dnn_inputs, 然后为每个任务创建一个门控网络输出最终融合Expert的门控向量。最后为每个任务都创建一个任务塔，并且不同任务塔的输入都是对应任务的门控向量和多个Expert融合后的向量。
mmoe.py 文件：

import tensorflow as tf

from .utils import (
    build_input_layer,
    build_group_feature_embedding_table_dict,
    concat_group_embedding,
)
from .layers import DNNs, PredictLayer


def build_mmoe_model(feature_columns, model_config):
    """
    构建多门控专家混合（MMoE）多任务排序模型。

    Args:
        feature_columns: FeatureColumn 列表
        model_config: 包含参数的字典：
            - task_names: 列表，任务名称（默认 ["is_click"]）
            - expert_nums: 整数，专家数量（默认 4）
            - expert_dnn_units: 列表，专家 DNN 隐藏单元（默认 [128, 64]）
            - gate_dnn_units: 列表，门控 DNN 隐藏单元（默认 [128, 64]）
            - task_tower_dnn_units: 列表，任务塔 DNN 隐藏单元（默认 [128, 64]）
            - dropout_rate: 浮点数，dropout 率（默认 0.1）

    Returns:
        (model, None, None): 排序模型元组
    """
    task_names = model_config.get("task_names", ["is_click"])
    expert_nums = model_config.get("expert_nums", 4)
    expert_dnn_units = model_config.get("expert_dnn_units", [128, 64])
    gate_dnn_units = model_config.get("gate_dnn_units", [128, 64])
    task_tower_dnn_units = model_config.get("task_tower_dnn_units", [128, 64])
    dropout_rate = model_config.get("dropout_rate", 0.1)

    # 输入层
    input_layer_dict = build_input_layer(feature_columns)

    # 分组嵌入
    group_embedding_feature_dict = build_group_feature_embedding_table_dict(
        feature_columns, input_layer_dict, prefix="embedding/"
    )

    # 连接不同组的嵌入向量作为网络的输入
    dnn_inputs = concat_group_embedding(group_embedding_feature_dict, "mmoe")

    # 创建多个专家
    expert_output_list = []
    for i in range(expert_nums):
        expert_output = DNNs(
            name=f"expert_{i}", units=expert_dnn_units, dropout_rate=dropout_rate
        )(dnn_inputs)
        expert_output_list.append(expert_output)
    expert_concat = tf.keras.layers.Lambda(lambda x: tf.stack(x, axis=1))(
        expert_output_list
    )  # (None, expert_num, dims)

    # 定义任务特定的门控网络
    task_tower_input_list = []
    for i, task_name in enumerate(task_names):
        gate_output = DNNs(
            name=f"task_{i}_gates", units=gate_dnn_units, dropout_rate=dropout_rate
        )(dnn_inputs)
        gate_output = tf.keras.layers.Dense(
            expert_nums, use_bias=False, activation="softmax", name=f"task_{i}_softmax"
        )(gate_output)
        gate_output = tf.keras.layers.Lambda(lambda x: tf.expand_dims(x, axis=-1))(
            gate_output
        )  # (None,expert_num, 1)
        gate_expert_output = tf.keras.layers.Lambda(lambda x: x[0] * x[1])(
            [gate_output, expert_concat]
        )
        gate_expert_output = tf.keras.layers.Lambda(
            lambda x: tf.reduce_sum(x, axis=1, keepdims=False)
        )(gate_expert_output)
        task_tower_input_list.append(gate_expert_output)

    # 不同任务通过门控融合多个专家
    task_output_list = []
    for i, task_name in enumerate(task_names):
        task_output_logit = DNNs(
            name=f"task_tower_{task_name}",
            units=task_tower_dnn_units + [1],
            dropout_rate=dropout_rate,
        )(task_tower_input_list[i])

        task_output_prob = PredictLayer(name=f"task_{task_name}")(task_output_logit)
        task_output_list.append(task_output_prob)

    # 构建模型，输出任务输出列表
    model = tf.keras.models.Model(
        inputs=list(input_layer_dict.values()), outputs=task_output_list
    )
    return model, None, None

1.3 PLE

原理

MMoE 通过为每个任务配备专属门控网络，在一定程度上缓解了多任务冲突问题。专属门控网络能够根据任务特性选择专家组合，从而使得不同任务可以关注不同的特征表示。但其架构仍存在一个根本性局限：所有专家对所有任务门控可见。这种“软隔离”设计在实践中仍面临两大挑战：

负迁移未根除：
- 干扰路径未切断：即使某个专家（如 $e_m$ ）被任务 $i$ 的门控高度加权而被任务 $j$ 的门控忽略，任务 $j$ 的梯度在反向传播时仍会流经 $e_m$ （因为 $e_m$ 是任务 $j$ 门控的可选项）。当任务冲突强烈时，这种“潜在通路”仍可能导致共享表征被污染。
- 专家角色模糊：MMoE缺乏机制强制专家明确分工。一个专家可能同时承载共享信息和多个任务的特定信息，成为冲突的“重灾区”。尤其在任务相关性低时，这种耦合会加剧负迁移。
门控决策负担重：
- 每个任务的门控需要在所有 $K$ 个专家上进行权重分配。当专家数量增加（通常需扩大 $K$ 以提升模型能力）时，门控网络面临高维决策问题，易导致训练不稳定或陷入次优解。
- 门控需要“费力”地从包含混杂信息（共享+所有任务特定）的专家池中筛选有用信息，增加了学习难度。

为解决上述问题，CGC结构被提出，其核心思想是通过硬性结构约束，显式分离共享知识与任务特定知识：

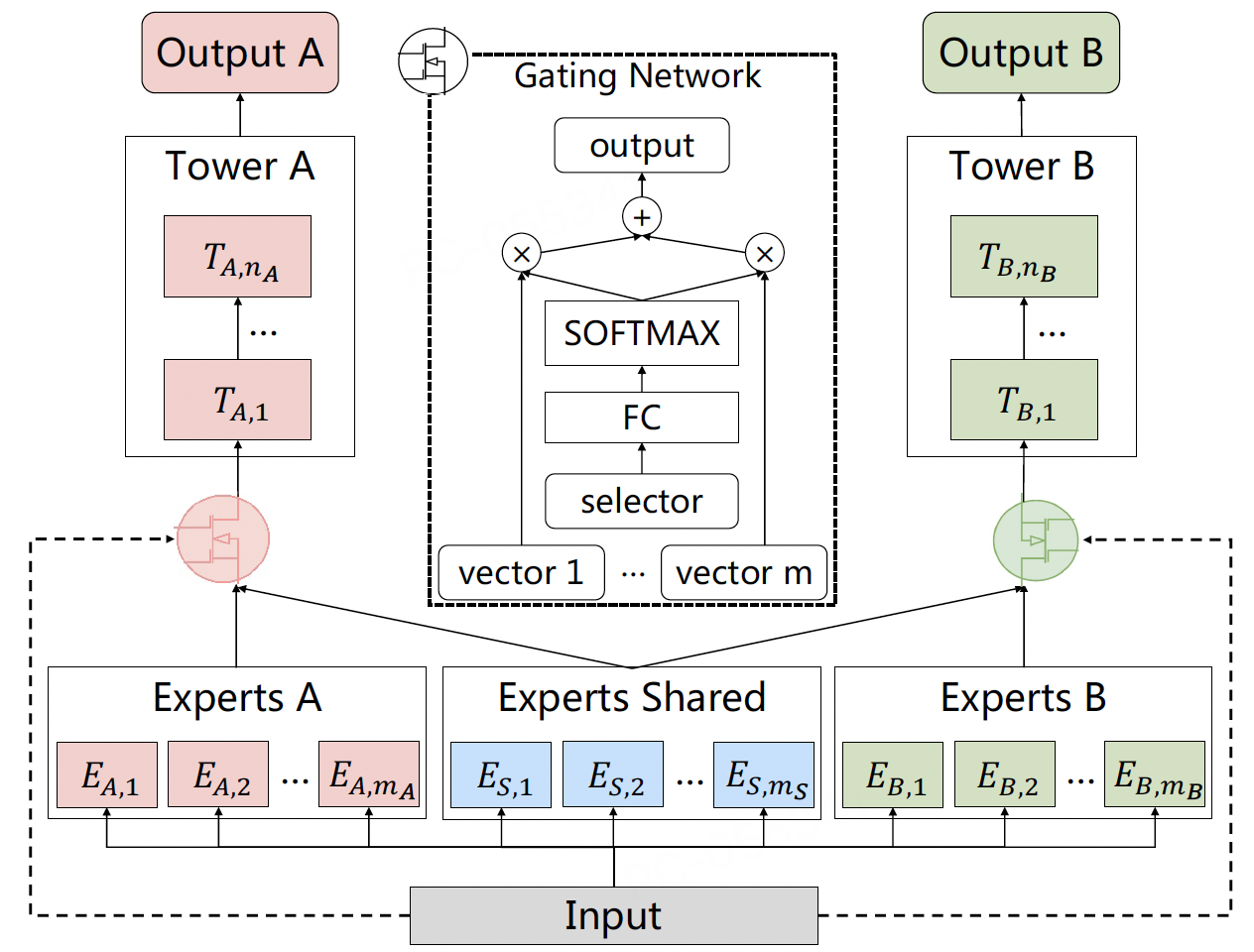
CGC网络结构

专家职责强制分离：

共享专家 (C-Experts)：一组专家仅负责学习所有任务的共性知识。设其数量为 $M$ ，输出为 ${\mathbf{c}_1, \mathbf{c}_2, ..., \mathbf{c}_M}$ 。
任务专家 (T-Experts)：每个任务 $t$ 拥有自己专属的专家组，仅负责学习该任务特有的知识或模式。设任务 $t$ 的专属专家数量为 $N_t$ ，输出为 ${\mathbf{t}_t^1, \mathbf{t}_t^2, ..., \mathbf{t}_t^{N_t}}$ 。

任务专属门控的输入限制：

任务 $t$ 的门控 $g_t$ 的输入被严格限制为：共享专家输出 ( ${\mathbf{c}k}{k=1}^M$ ) + 本任务专属专家输出 ( ${\mathbf{t}t^j}{j=1}^{N_t}$ )。
物理切断干扰路径：任务 $t$ 的门控完全无法访问其他任务 $s (s \neq t)$ 的专属专家 ${\mathbf{t}_s^j}$ 。同样，任务 $s$ 的梯度绝不会更新任务 $t$ 的专属专家参数。

CGC门控的计算如下：

$g_t(\mathbf{x}) = \text{softmax}\Big(\mathbf{W}_t \cdot \mathbf{x} + \mathbf{b}_t\Big) \quad$

$\mathbf{h}_t = \sum_{k=1}^{M} g_{t,k} \cdot \mathbf{c}_k + \sum_{j=1}^{N_t} g_{t, M+j} \cdot \mathbf{t}_t^j$

$\hat{y}_t = f_t(\mathbf{h}_t)$

其中：

$\mathbf{W}_t, \mathbf{b}_t$ ：任务 $t$ 门控的参数。
$g_{t,k}$ ：分配给第 $k$ 个共享专家的权重。
$g_{t, M+j}$ ：分配给任务 $t$ 第 $j$ 个专属专家的权重。

CGC解决了知识分离的核心问题，但其本质是单层结构，表征学习深度有限。受深度神经网络逐层抽象特征的启发，PLE (Progressive Layered Extraction) 将多个CGC单元纵向堆叠，形成深层架构，实现渐进式知识提取与融合。

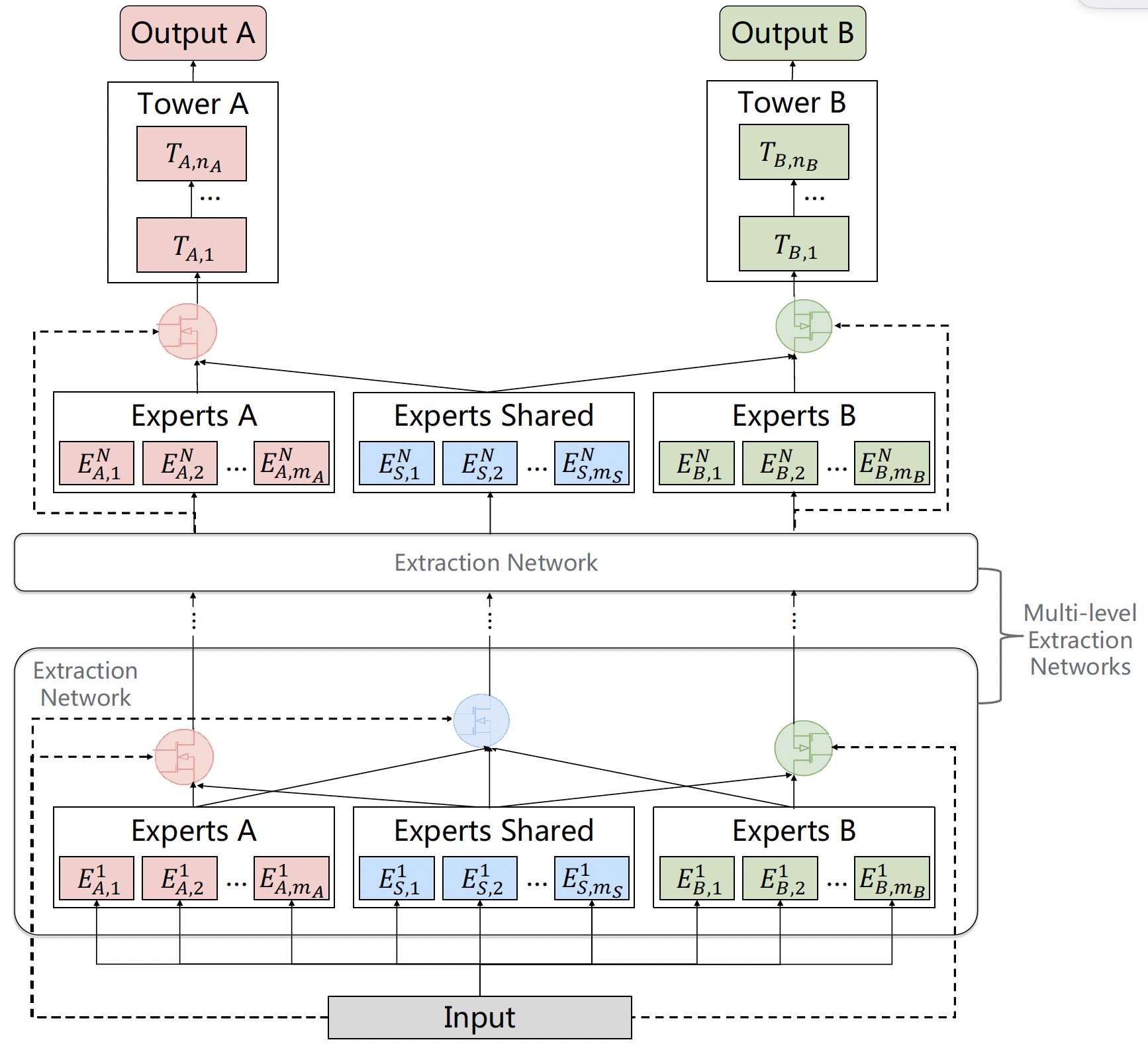
PLE网络结构

第1层 (输入层 CGC)：
- 输入：原始特征 $\mathbf{x}$ 。
- 结构：一个标准的CGC模块（包含 $M^{(1)}$ 个C-Experts, 每个任务 $t$ 有 $N_t^{(1)}$ 个T-Experts, 以及对应的门控 $g_t^{(1)}$ ）。
- 输出：每个任务获得初步融合表示 $\mathbf{h}_t^{(1)}$ （或更常见的是，该层所有专家（C+T）的输出被拼接/收集起来作为下一层输入）。
第 $l$ 层 ( $l \geq 2$ ) CGC：
- 输入关键点：第 $l$ 层的输入是第 $l-1$ 层所有专家（包括所有C-Experts和所有任务的T-Experts）的输出。设第 $l-1$ 层总专家数为 $E^{(l-1)}$ ，则输入向量维度相应增加。
- 结构：一个新的CGC模块（包含 $M^{(l)}$ 个C-Experts, 每个任务 $t$ 有 $N_t^{(l)}$ 个T-Experts, 以及门控 $g_t^{(l)}$ ）。
- 处理：在本层输入特征（即上一层更丰富的表征）上，再次进行显式的知识分离（新的C-Experts学习更深层共享模式，新的T-Experts学习更深层任务特定模式）和融合（通过新的门控）。
- 输出：任务 $t$ 的当前层表示 $\mathbf{h}_t^{(l)}$ 或收集所有专家输出。
输出层 (第 $L$ 层)：
- 最后一层( $L$ )各任务的门控输出 $\mathbf{h}_t^{(L)}$ 送入各自的任务专属塔网络（Tower） $f_t$ ，得到最终预测 $\hat{y}_t = f_t(\mathbf{h}_t^{(L)})$ 。

代码

ple.py 文件：

import tensorflow as tf
import itertools

from .utils import (
    build_input_layer,
    build_group_feature_embedding_table_dict,
    concat_group_embedding,
)
from .layers import DNNs, PredictLayer


def cgc_net(
    input_list,
    task_num,
    task_expert_num,
    shared_expert_num,
    task_expert_dnn_units,
    shared_expert_dnn_units,
    task_gate_dnn_units,
    shared_gate_dnn_units,
    leval_name=None,
    is_last=False,
):
    """CGC结构
    input_list: 每个任务都有一个输入，这些任务的输入都是共享的，为了方便处理，给每个任务都复制了一份
    is_last: 主要是判断是否是最后一层CGC，如果是的话，就不需要把共享部分添加到输出中了
    """

    # 创建每个任务的任务专家
    task_expert_list = []
    for i in range(task_num):
        task_i_expert_list = []
        for j in range(task_expert_num):
            expert_dnn = DNNs(
                task_expert_dnn_units,
                name=f"{leval_name}_task_{str(i)}_expert_{str(j)}",
            )(input_list[i])
            task_i_expert_list.append(expert_dnn)
        task_expert_list.append(task_i_expert_list)

    # 创建所有任务的共享专家
    shared_expert_list = []
    for i in range(shared_expert_num):
        expert_dnn = DNNs(
            shared_expert_dnn_units, name=f"{leval_name}_shared_expert_{str(i)}"
        )(input_list[-1])
        shared_expert_list.append(expert_dnn)

    # 创建每个任务的融合门控
    task_gate_list = []
    fusion_expert_num = task_expert_num + shared_expert_num
    for i in range(task_num):
        gate_dnn = DNNs(task_gate_dnn_units, name=f"{leval_name}_task_{str(i)}_gate")(
            input_list[i]
        )
        gate_dnn = tf.keras.layers.Dense(
            fusion_expert_num, use_bias=False, activation="softmax"
        )(gate_dnn)
        gate_dnn = tf.keras.layers.Lambda(lambda x: tf.expand_dims(x, axis=-1))(
            gate_dnn
        )  # (None, gate_num, 1)
        task_gate_list.append(gate_dnn)

    # CGC输出结果
    cgc_output_list = []
    for i in range(task_num):
        cur_experts = task_expert_list[i] + shared_expert_list
        expert_concat = tf.keras.layers.Lambda(lambda x: tf.stack(x, axis=1))(
            cur_experts
        )  # None, gate_num, dim
        cur_gate = task_gate_list[i]
        task_gate_fusion_dnn = tf.keras.layers.Lambda(
            lambda x: tf.reduce_sum(x[0] * x[1], axis=1, keepdims=False)
        )(
            [cur_gate, expert_concat]
        )  # None, dim
        cgc_output_list.append(task_gate_fusion_dnn)

    # 如果不是最后一层还需要更新共享专家下一层的输入，也就是当前层需要融合所有任务和共享专家
    if not is_last:
        cur_experts = (
            list(itertools.chain.from_iterable(task_expert_list)) + shared_expert_list
        )
        cur_expert_num = len(cur_experts)
        expert_concat = tf.keras.layers.Lambda(lambda x: tf.stack(x, axis=1))(
            cur_experts
        )  # None, cur_expert_num, dim
        shared_gate_dnn = DNNs(shared_gate_dnn_units, name=f"{leval_name}_shared_gate")(
            input_list[-1]
        )
        shared_gate_dnn = tf.keras.layers.Dense(
            cur_expert_num, use_bias=False, activation="softmax"
        )(
            shared_gate_dnn
        )  # None, cur_expert_num
        shared_gate = tf.keras.layers.Lambda(lambda x: tf.expand_dims(x, -1))(
            shared_gate_dnn
        )  # None, cur_expert_num, 1
        shared_gate_fusion_output = tf.keras.layers.Lambda(
            lambda x: tf.reduce_sum(x[0] * x[1], axis=1, keepdims=False)
        )([shared_gate, expert_concat])
        cgc_output_list.append(shared_gate_fusion_output)
    return cgc_output_list


def build_ple_model(feature_columns, model_config):
    """
    构建PLE（渐进式分层提取）多任务排序模型。

    参数:
        feature_columns: FeatureColumn列表
        model_config: 包含参数的字典:
            - task_names: 列表，任务名称（默认["is_click"]）
            - ple_level_nums: 整数，PLE层数（默认1）
            - task_expert_num: 整数，任务专用专家数量（默认4）
            - shared_expert_num: 整数，共享专家数量（默认2）
            - task_expert_dnn_units: 列表，任务专家DNN隐藏单元（默认[128, 64]）
            - shared_expert_dnn_units: 列表，共享专家DNN隐藏单元（默认[128, 64]）
            - task_gate_dnn_units: 列表，任务门控DNN隐藏单元（默认[128, 64]）
            - shared_gate_dnn_units: 列表，共享门控DNN隐藏单元（默认[128, 64]）
            - task_tower_dnn_units: 列表，任务塔DNN隐藏单元（默认[128, 64]）
            - dropout_rate: 浮点数，dropout率（默认0.1）

    返回:
        (model, None, None): 排序模型元组
    """
    # 从model_config中提取参数
    task_names = model_config.get("task_names", ["is_click"])
    ple_level_nums = model_config.get("ple_level_nums", 1)
    task_expert_num = model_config.get("task_expert_num", 4)
    shared_expert_num = model_config.get("shared_expert_num", 2)
    task_expert_dnn_units = model_config.get("task_expert_dnn_units", [128, 64])
    shared_expert_dnn_units = model_config.get("shared_expert_dnn_units", [128, 64])
    task_gate_dnn_units = model_config.get("task_gate_dnn_units", [128, 64])
    shared_gate_dnn_units = model_config.get("shared_gate_dnn_units", [128, 64])
    task_tower_dnn_units = model_config.get("task_tower_dnn_units", [128, 64])
    dropout_rate = model_config.get("dropout_rate", 0.1)

    # 输入层
    input_layer_dict = build_input_layer(feature_columns)

    # 分组嵌入
    group_embedding_feature_dict = build_group_feature_embedding_table_dict(
        feature_columns, input_layer_dict, prefix="embedding/"
    )

    # 连接不同组的嵌入向量作为网络的输入
    dnn_inputs = concat_group_embedding(group_embedding_feature_dict, "ple")

    task_num = len(task_names)
    ple_input_list = [dnn_inputs] * (task_num + 1)

    for i in range(ple_level_nums):
        if i == ple_level_nums - 1:
            cgc_output_list = cgc_net(
                ple_input_list,
                task_num,
                task_expert_num,
                shared_expert_num,
                task_expert_dnn_units,
                shared_expert_dnn_units,
                task_gate_dnn_units,
                shared_gate_dnn_units,
                leval_name=f"cgc_level_{str(i)}",
                is_last=True,
            )
        else:
            cgc_output_list = cgc_net(
                ple_input_list,
                task_num,
                task_expert_num,
                shared_expert_num,
                task_expert_dnn_units,
                shared_expert_dnn_units,
                task_gate_dnn_units,
                shared_gate_dnn_units,
                leval_name=f"cgc_level_{str(i)}",
                is_last=False,
            )
            ple_input_list = cgc_output_list

    # 构建任务专用塔
    task_output_list = []
    for i in range(task_num):
        task_output_logit = DNNs(
            name=f"task_tower_{task_names[i]}",
            units=task_tower_dnn_units + [1],
            dropout_rate=dropout_rate,
        )(cgc_output_list[i])

        task_output_prob = PredictLayer(name=f"task_{task_names[i]}")(task_output_logit)
        task_output_list.append(task_output_prob)

    # 构建模型，输出任务输出列表
    model = tf.keras.models.Model(
        inputs=list(input_layer_dict.values()), outputs=task_output_list
    )
    return model, None, None

性能对比

+----------------+----------------+---------------+-----------------+-------------+-----------------+----------------+------------------+--------------+---------------------+--------------------+----------------------+
|   model        |   auc_is_click |   auc_is_like |   auc_long_view |   auc_macro |   gauc_is_click |   gauc_is_like |   gauc_long_view |   gauc_macro |   val_user_is_click |   val_user_is_like |   val_user_long_view |
+================+================+===============+=================+=============+=================+================+==================+==============+=====================+====================+======================+
| shared_bottom  |         0.6002 |        0.4335 |          0.4455 |      0.4931 |          0.5734 |         0.4358 |           0.4514 |       0.4869 |                 928 |                530 |                  925 |
+----------------+----------------+---------------+-----------------+-------------+-----------------+----------------+------------------+--------------+---------------------+--------------------+----------------------+
| mmoe           |         0.6018 |        0.4447 |          0.4323 |      0.4929 |          0.5736 |         0.4463 |           0.4595 |       0.4931 |                 928 |                530 |                  925 |
+----------------+----------------+---------------+-----------------+-------------+-----------------+----------------+------------------+--------------+---------------------+--------------------+----------------------+
| ple            |         0.5928 |          0.42 |          0.4575 |      0.4901 |          0.5713 |         0.4438 |           0.4638 |        0.493 |                 928 |                530 |                  925 |
+----------------+----------------+---------------+-----------------+-------------+-----------------+----------------+------------------+--------------+---------------------+--------------------+----------------------+

2、任务依赖建模

前面介绍的多目标方法主要解决任务间的相关性冲突，但现实场景中任务间往往存在明确的依赖关系。用户行为具有天然的时序性：曝光→点击→转化，这种严格的依赖关系带来了新的挑战。

传统方法在处理这种依赖时面临两个核心问题：样本选择偏差（CVR模型在点击样本上训练，却要在全量样本上预测）和数据稀疏性（转化事件极其稀少）。

本节介绍两个全空间建模方法：ESMM解决经典的CTR-CVR联合建模问题，ESM2将思想扩展到更复杂的多阶段行为链路。

2.1 ESMM

原理

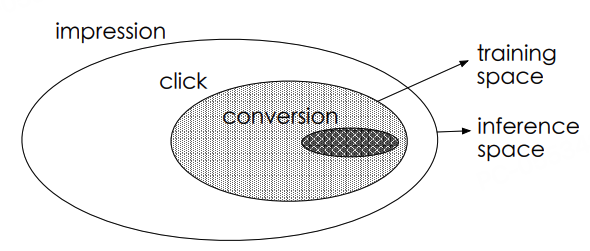
点击率和转化率预估的样本空间

在推荐系统的用户行为链中，存在严格的时序依赖关系。以电商场景为例：

$\text{曝光(Impression)} \rightarrow \text{点击(Click)} \rightarrow \text{转化(Conversion)}$

这种链式结构导致两个关键问题：

样本选择偏差(Sample Selection Bias)：传统CVR模型仅在点击样本（CTR正样本）上训练，但线上预估需覆盖全量曝光样本，训练/预估样本分布差异导致泛化能力下降
数据稀疏性(Data Sparsity)：转化样本量 = 曝光量 × CTR × CVR，典型场景：CTR≈2%, CVR≈0.5% → 转化样本仅为曝光的万分之一，稀疏样本难以支撑复杂模型学习

ESMM (Entire Space Multi-task Model) 通过概率图约束重建任务关系：

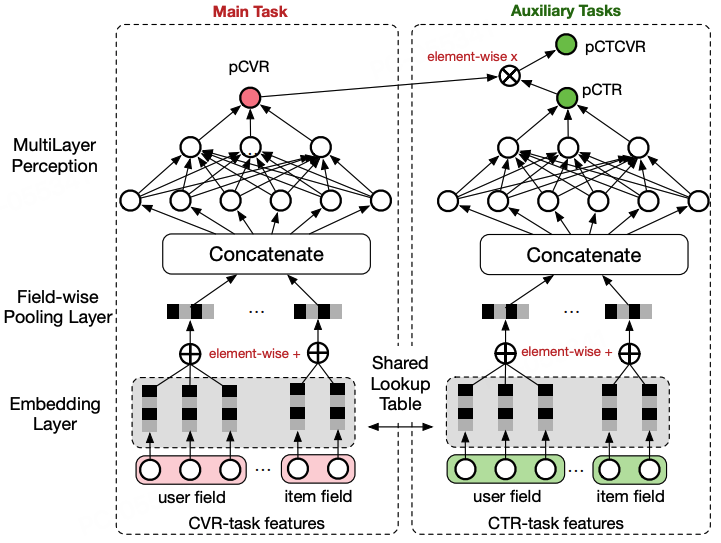
ESMM模型结构

输入层：全量曝光样本特征 $\mathbf{x}$
共享表征层：基础特征提取模块（原论文中采用的是Shared-Bottom的简单共享结构，也可将其直接替换成MMoE、PLE等复杂的底层共享模型）
任务塔层：
- CTR Tower：预测点击概率 $pCTR = f_{ctr}(\mathbf{h})$
- CVR Tower：预测转化概率 $pCVR = f_{cvr}(\mathbf{h})$
输出层：
- $pCTR = f_{ctr}(\mathbf{h})$ ， $pCVR = f_{cvr}(\mathbf{h})$ ，其中 $pCVR$ 不用用来计算Loss
- $pCTCVR = pCTR \times pCVR$ ，该值用来计算从曝光空间到转化的Loss

损失函数的设计：

$\mathcal{L} = \mathcal{L}_{CTR} + \mathcal{L}_{CTCVR}$

其中：

$\mathcal{L}_{CTR}$ 是标准的二分类交叉熵损失，使用全量曝光样本：

$\mathcal{L}_{CTR} = - \frac{1}{N} \sum_{i=1}^N \left[ y_i^{click} \log(pCTR_i) + (1 - y_i^{click}) \log(1 - pCTR_i) \right]$

$\mathcal{L}_{CTCVR}$ 是CTCVR任务的交叉熵损失，通过概率转化公式 $pCTCVR = pCTR \times pCVR$ ，使得CVR Tower的参数更新是在曝光空间下进行的：

$\mathcal{L}_{CTCVR} = - \frac{1}{N} \sum_{i=1}^N \left[ y_i^{click} \cdot y_i^{conv} \log(pCTCVR_i) + (1 - y_i^{click} \cdot y_i^{conv}) \log(1 - pCTCVR_i) \right]$

ESMM的核心创新在于CVR塔的梯度来源,CVR塔同时接收两种梯度：

$\nabla_{CVR} = \underbrace{\frac{\partial \mathcal{L}_{CTCVR}}{\partial pCTCVR} \cdot pCTR}_{\text{全空间梯度}} + \underbrace{\frac{\partial \mathcal{L}_{shared}}{\partial \mathbf{h}}}_{\text{共享层梯度}}$

代码

esmm.py 文件：

import tensorflow as tf

from .utils import (
    build_input_layer,
    build_group_feature_embedding_table_dict,
    concat_group_embedding,
)
from .layers import DNNs, PredictLayer


def build_esmm_model(feature_columns, model_config):
    """
    构建ESMM（全空间多任务模型）排序模型。

    参数:
        feature_columns: FeatureColumn列表
        model_config: 包含以下参数的字典:
            - task_names: 列表，任务名称（默认 ["is_click", "is_like"]）
            - task_tower_dnn_units: 列表，任务塔DNN隐藏单元数（默认 [128, 64]）
            - dropout_rate: 浮点数，丢弃率（默认 0.1）

    返回:
        (model, None, None): 排序模型元组
    """
    task_names = model_config.get("task_names", ["is_click", "is_like"])
    task_tower_dnn_units = model_config.get("task_tower_dnn_units", [128, 64])
    dropout_rate = model_config.get("dropout_rate", 0.1)

    # 输入层
    input_layer_dict = build_input_layer(feature_columns)

    # 分组嵌入
    group_embedding_feature_dict = build_group_feature_embedding_table_dict(
        feature_columns, input_layer_dict, prefix="embedding/"
    )

    # 连接不同组的嵌入向量作为网络的输入
    dnn_inputs = concat_group_embedding(group_embedding_feature_dict, "dnn")

    # CTR塔（第一个任务）
    ctr_output_logits = DNNs(
        name="ctr_dnn", units=task_tower_dnn_units + [1], dropout_rate=dropout_rate
    )(dnn_inputs)

    # CVR塔（第二个任务）
    cvr_output_logits = DNNs(
        name="cvr_dnn", units=task_tower_dnn_units + [1], dropout_rate=dropout_rate
    )(dnn_inputs)

    # 应用预测层
    ctr_output_prob = PredictLayer(name="ctr_output")(ctr_output_logits)
    cvr_output_prob = PredictLayer(name="cvr_output")(cvr_output_logits)

    # CTCVR = CTR * CVR（ESMM核心思想）
    ctcvr_output_prob = tf.keras.layers.Lambda(lambda x: tf.multiply(x[0], x[1]))(
        [ctr_output_prob, cvr_output_prob]
    )

    # 构建模型，输出任务输出列表
    model = tf.keras.models.Model(
        inputs=list(input_layer_dict.values()),
        outputs=[ctr_output_prob, ctcvr_output_prob],
    )
    return model, None, None

2.2 ESM2

原理

ESMM成功解决了曝光→点击→转化这一两阶段行为链路的样本偏差问题，但在真实工业场景中，用户行为链路往往更长更复杂。

用户下单链路图

如图所示，用户从曝光到转化可能会有非常多条的路径，例如 曝光->点击->加入购物车->购买、曝光->点击->加入许愿池->加入购物车->购买等。为了方便后续建模，对点击后的行为分解做了进一步的简化，将加入购物车、加入心愿单归并为决定行为（Deterministic Action，DAction），将其余行为归并为其他行为（Other Action，OAction）

简化后的用户下单链路图

为了更好理解后续建模时的数学表达，先对简化后图中的过程，做进一步的数学表示。

$y_1=p(\text{点击}|\text{曝光})$
$y_2=p(\text{决定行为}|\text{点击})$
$y_3=p(\text{购买}|\text{决定行为})$
$y_4=p(\text{购买}|\text{其他行为})$

根据上述定义，更便于理解ESM2模型的结构图：

ESM2模型结构图

ESM2模型有四个塔，分别用来预测上述的 $y_1,y_2,y_3$ 和 $y_4$ ，对于这四个塔的输出并不是算4个Loss，而是分别计算曝光->点击、曝光->决定行为和曝光->购买这三个Loss。可以很明显的看出，这三个Loss都是在曝光空间上计算的，和ESMM在曝光空间优化CVR有着异曲同工之处。下面对于上述的三个Loss做简单的介绍，下面的 $BCE_{Loss}$ 表示的是二元交叉熵损失。

$L_{ctr}$ 点击率预估损失：

$\begin{aligned} L_{ctr} &= \frac{1}{N} \text{BCE}_{\text{Loss}}(y_{\text{isClick}}^i, \text{pCTR}_i) \\ & = \frac{1}{N} \text{BCE}_{\text{Loss}}(y_{\text{isClick}}^i, \text{y}_1^i) \end{aligned}$

$L_{ctavr}$ 点击且决定行为概率预估损失：

$\begin{aligned} L_{ctavr} &= \frac{1}{N} \text{BCE}_{\text{Loss}}(y_{\text{isDAction}}^i, \text{pCTAVR}_i) \\ & = \frac{1}{N} \text{BCE}_{\text{Loss}}(y_{\text{isDAction}}^i, \text{y}_1^i \cdot \text{y}_2^i) \end{aligned}$

$L_{ctcvr}$ 转化率预估损失：

$\begin{aligned} L_{ctcvr} &= \frac{1}{N} \text{BCE}_{\text{Loss}}(y_{\text{isPurchuse}}^i, \text{pCTCVR}_i) \\ & = \frac{1}{N} \text{BCE}_{\text{Loss}}(y_{\text{isPurchuse}}^i, \text{y}_1^i (\text{y}_2^i \cdot \text{y}_3^i + (1 - \text{y}_2^i) \cdot \text{y}_4^i)) \end{aligned}$

从简化后的用户下单链路图中可以看出，用户最终转化是有两条链路的，分别为：

曝光->点击->决定行为->购买=> $y_1 \cdot y_2 \cdot y_3$
曝光->点击->其他行为->购买=> $y_1 \cdot (1-y_2) \cdot y_4$

合并上述两条链路的结果就可以得到 $pCTCVR=y_1(y_2 \cdot y_3 + (1-y_2) \cdot y_4)$

最终上述三个损失通过加权融合的方式进行联合优化，

$L_{final} = w_{ctr} \cdot L_{ctr} + w_{ctavr} \cdot L_{ctavr} + w_{ctcvr} \cdot L_{ctcvr}$

其中 $w_{ctr},w_{ctavr},w_{ctcvr}$ 分别为三个损失的权重。

ESM2通过这种多阶段的概率乘积方式，将复杂的用户行为链路分解为多个可建模的子任务，同时确保每个任务都在曝光空间中进行联合优化。这种设计不仅有效解决了样本选择偏差问题，还通过共享底层特征表征，降低了数据稀疏性对模型性能的影响。更重要的是，ESM2提供了一种通用的建模思路，可以灵活扩展到更长的行为链路和更多样化的用户决策路径中。

性能

+----------------+----------------+---------------+-------------+-----------------+----------------+--------------+---------------------+--------------------+
| model          |   auc_is_click |   auc_is_like |   auc_macro |   gauc_is_click |   gauc_is_like |   gauc_macro |   val_user_is_click |   val_user_is_like |
+================+================+===============+=============+=================+================+==============+=====================+====================+
| esmm           |         0.5983 |        0.6552 |      0.6267 |          0.5719 |         0.5811 |       0.5765 |                 928 |                530 |
+----------------+----------------+---------------+-------------+-----------------+----------------+--------------+---------------------+--------------------+

3、多目标损失融合

多目标往往伴随着多个损失的联合优化，这类优化方法更多的考虑的是在模型结构已经确定的条件下，结合任务的特点对模型进行训练和参数优化。简单的多目标Loss优化，是通过手工结合业务经验设定不同损失的权重，将多个损失加权为一个进行优化，如下所示：

$Loss_{total} = \sum_i w_i L_i$

其中， $L_i$ 和 $w_i$ 分别表示第i个任务的损失及对应的权重。

在多目标建模中，当模型结构确定后，损失函数融合策略成为决定模型性能的关键因素。传统的手工加权方法存在三个本质性缺陷：

量级失衡问题：不同任务的损失值量级差异显著（如CTR损失通常在0.1-0.5，CVR损失可达2.0+），导致大损失主导优化方向
收敛异步问题：稀疏任务收敛慢，密集任务收敛快，造成过拟合与欠拟合并存
梯度冲突问题：任务梯度方向不一致时产生抵消效应（如CTR与CTR任务梯度夹角>90°）

下面系统解析三大主流优化方法，包含理论框架、实现机制与工程实践。

3.1 Uncertainty Weight：基于不确定性的自适应加权

基于不确定性加权损失（Uncertainty Weighted Loss, UWL）。UWL的核心思想是根据任务的不确定性动态调整权重，具体来说，任务的损失越大，分配的权重越小。论文指出，在任务训练过程中存在两种不确定性：一种是认知不确定性（epistemic uncertainty），源于数据的缺乏；另一种是偶然不确定性（aleatoric uncertainty），源于数据本身或任务本身的特性。
在UWL中，任务的损失函数可以表示为：

$Loss = \approx \frac{1}{2\sigma_1^2} \mathcal{L}_1(\mathbf{W}) + \frac{1}{\sigma_2^2} \mathcal{L}_2(\mathbf{W}) + \log \sigma_1 + \log \sigma_2$

其中， $\sigma$ 表示的是任务的不确定性(uncertainty),是可学习的参数。从公式可以看出，当loss较大且 $\sigma$ 较小时， $\frac{1}{2\sigma^2} \mathcal{L}(\mathbf{W})$ 会很大，损失函数在优化的时候就会将其往小了优化。可以直观的理解为，模型不会让任务往不确定性较大的方向大幅更新参数。

3.2 GradNorm：梯度标准化方法

在多任务优化的过程中，不同的任务loss的量级是不一样的，这样带来的问题就是loss大的任务梯度更新的幅度也会更大，进而导致模型在学习的过程中被loss大的任务主导带偏整个模型。此外，不同的任务由于数据分布的原因，loss的收敛速度也是不同的。为了同时考虑loss的量级和训练的速度。GradNorm在模型优化过程中除了正常的任务loss外，还引入了一个gradient loss，该loss通过梯度下降的方式来更新不同任务的loss权重。并且这两个loss是单独优化的，而不是简单的相加得到一个loss去综合优化。

在介绍gradient loss之前，我们先来看一下如何定义梯度的量级和loss的学习速度。

$G_{W}^{(i)}(t) \, = \, \|\nabla_{W} w_{i}(t) L_{i}(t)\|_{2}$

$\overline{G}_{W}(t) \, = \, E_{\text{task}}[G_{W}^{(i)}(t)]$

其中 $W$ 是所有任务loss对多个任务最后一层共享参数， $G_{W}^{(i)}(t)$ 表示任务 $i$ 加权后的Loss，对共享参数 $W$ 的梯度，该值较大时表示loss $i$ 当前的梯度量级较大， $\overline{G}_{W}(t)$ 表示所有任务对共享参数梯度的均值。

$\tilde{L}_i(\tilde{t}) = L_i(t) / L_i(0)$

$r_i(t) = \frac{\tilde{L}_i(t)}{E_{\text{task}}[\tilde{L}_i(t)]}$

$L_i(t)$ 表示的是训练的第t时刻，任务 $i$ 的Loss值，所以 $\tilde{L}_i(\tilde{t})$ 表示的是任务 $i$ 在第t时刻的相对第0时刻的损失比率，该值如果越小的话则代表该任务loss收敛的比较快，训练速度较大。 $r_i(t)$ 则是在 $L_i(t)$ 的基础上做了一次归一化，让所有任务之间的速率相对可以比较，同样也是值越小表示任务的训练速度越快。

最终的梯度损失函数定义为如下表达式：

$L_{\text{grad}}(t; w_i(t)) = \sum_i \left| G_W^{(i)}(t) - \overline{G}_W(t) \times [r_i(t)]^\alpha \right|_1$

梯度损失函数综合了上述定义的梯度量级和学习速度，直观理解就是当某个loss的梯度非常大时，该loss的值也会较大进而会将该loss的权重降的更小，避免了梯度大的loss主导了模型的学习。同理当某个任务学习的速度较快时，即 $r_i(t)$ 较小，梯度loss也会变得更大，进而使得该loss的权重会变得更小，阻止某个任务过快的收敛。

3.3 Pareto Optimization：帕累托优化框架

在多任务学习中，当不同任务的梯度方向存在根本性冲突时（即优化任务A必然损害任务B），我们面临帕累托边界优化问题。传统加权平均方法在此场景下失效，需要专门的优化框架寻找帕累托最优解集：

$\min_{\theta} \mathbf{L}(\theta) = \min_{\theta} (\mathcal{L}_1(\theta), \mathcal{L}_2(\theta), ..., \mathcal{L}_T(\theta))$

其中帕累托最优解定义为：不存在其他解能在不损害至少一个任务的情况下改进任一任务。

帕累托最优损失融合核心思想：

将多目标损失合并为加权和，并利用 KKT 条件动态调整权重，使优化方向指向帕累托前沿：

$\mathcal{L}(\theta) = \sum_{i=1}^{K} w_i \mathcal{L}_i (\theta)$

其中 $w_i$ 为可学习的权重，满足 $\sum w_i = 1$ 且 $w_i \geq c_i$ （ $c_i$ 为权重下限）。

优化步骤（分两步迭代）：

固定权重，更新模型参数 $\theta$ ：通过梯度下降最小化加权损失 $\mathcal{L}(\theta)$ ，即常规的模型训练步骤。
固定模型，更新权重 $w_i$
- 目标：求解权重 $w_i$ ，使加权梯度的二范数最小化（满足 KKT 条件）：
$\min _{w}\left\|\sum_{i=1}^{K} w_{i} \nabla_{\theta} \mathcal{L}_{i}(\theta)\right\|_{2}^{2}$
- 约束条件： $\sum w_i = 1$ ， $w_i \geq c_i$ 。
- 松弛与投影：
  - 引入变量 $\tilde{w}_i = w_i - c_i$ ，将不等式约束转化为非负约束。
  - 先忽略 $\tilde{w}_i \geq 0$ ，求解带等式约束的二次规划问题。
  - 对解 $\tilde{w}^*$ 进行投影，确保其非负性（投影问题可通过闭式解快速求解）：
  $\min _{\tilde{w}}\|\tilde{w}-\tilde{w}^*\|_2^2 \quad \text{s.t.} \quad \sum \tilde{w}_i=1-\sum c_i, \tilde{w}_i \geq 0$