mathAI

论文：Defending Attacks on Anti-fraud Model with Generative Graph Representations

基于生成图表示的金融反欺诈模型对抗防御方法

Abstract

• Fraud detection is a typical data mining mission in the field of finance. In recent years, due to their capability of mining hidden associations between entities, graph neural networks (GNNs) have been widely applied to detect financial fraudsters.
• However, GNNs are fragile in their data aggregation process and will be attacked on purpose by fraudsters, therefore, some other pioneers have explored methods to enhance the robustness of GNN-based fraud detection models. But most existing models based on ideal settings, as real-life criminals tend to attack as far as they can reach, struggle to establish a unified effective approach for attacked and unattacked data of different scales in realistic scenarios.
• Furthermore, mainstream robust defense models indiscriminately modifying and truncating data will lose important information of the major unattacked parts in the original graph, which lowers their overall fraud detection precision.
• Therefore, in this work, we propose a novel generative fraud detection framework called GSRGNN. In particular, we first design a generative structure to obtain augmented node features. Then we prioritize the nodes with high degrees to create a more stable graph structure on local distributions. Finally, we pass the enhanced features and structure with the input ones in pairs through GNN layers, and create synthetic representations with abundant information and sufficient resistance to perturbations for subsequent fraud detection. In addition, we also design a novel black-box attack algorithm to realistically imitate the perturbations conducted by fraudsters on graph features and structure. Experiments on the world’s leading electronic trading platform and public anti-fruad datasets demonstrate the outstanding performance of our proposed method compared with those state-of-the-art models, showing its superiority in precision and robustness on financial fraud detection missions.

Index Terms—Generative graph learning, financial fraud detection, adversarial attack and defense.

• 背景：GNN广泛应用于金融欺诈检测方面。但是，传统经典GNN在数据聚合阶段中极易受到攻击并不断传播下去。目前已有的对抗模型都是在理想对抗环境中建模，但现实欺诈者往往是灵活多变的攻击手法，因此难以为现实情景不同规模的受攻击和未受攻击场景建立一个统一高效的方法。
• 同时，主流鲁棒防御模型不加区分地修改和截断数据，会丢失原始图中主要未受攻击部分的重要信息，从而降低其整体欺诈检测精度。
• 因此，我们换一个角度，GSRGNN框架是，
  • 特征增强（重构干净节点）：先通过一个生成模块获取增强的干净节点特征。
  • 结构增强（局部高阶邻居结构增强）：再使用节点阶数作为信赖值，以获得在各自局部图上的稳定结构。
  • 上述形成一张新图。
  • 最后，将新的生成图和原始图一并作为输入进入下一层生成得到综合图特征。
• 解释：
  1. 前序操作相当于进行欺诈的初步扫描和特征升维，把每个节点的特征放大，把可信节点的结构稳定住。（要知道，图神经网络本身是只做聚合和传播的，并不会涉及到单节点的特征升维降维问题）
  2. 后续把新图和原图一并输入，这和残差连接的思想很像，我们希望有新的更强的图结构，但是也不希望只依赖新图。原图数据的存在可以保证在新图失效的情况下，仍然保有基本的baseline效果，而不是整个模型完全失效。并且，在后续图神经网络传播过程中，新图和原图的对应也可能会产生新的数据挖掘效果。
  3. 为什么选局部？因为攻击者本身实际上也只能看到自己周围的节点，也就是说攻击本身是局部的，我们只需要对每个局部图进行修正稳定就足够了。局部攻击也是后续模拟真实攻击的创新攻击方法，这是更加接近现实情景的攻击方法，而不是不加区分地全图修改。
  4. 为什么选高阶？因为高阶节点往往是比较稳定的，难以被攻击者的扰动产生影响。

Proposed methods

In this section, we introduce our proposed methods in detail.

• First, we present the background of our work and the definitions of symbols and problems.
• Second, we introduce the attack algorithms simulating real-life scenarios.
• Third, we explain the overall structure of our novel GNN-based framework called GSRGNN.
  After that, we introduce the generative module which is used for the augmentation of node features. Then, we present the designed strategies to enhance graph structure. Lastly, we introduce the synthesis of the enhanced and original representations, and the combination and optimization strategy of the proposed modules.

• 背景、模拟现实情景的攻击算法、介绍GSRGNN
• 其中GSRGNN：
  1. 生成模块：节点特征聚合
  2. 稳定策略：增强局部图结构
  3. 综合方法：增强图和原始图的综合
• 最后，还介绍提出模型的合成和优化策略

A. 背景

• 随着GNN应用越来越多，对应欺诈者也会有新手段。
• 两种：
  1. 避免暴露明显的欺诈交易特征：对特征的攻击
  2. 与中间商交易或盗用他人身份与无辜的人建立关系：对结构的攻击
• 对应现实情景下，欺诈者的感受野 Receptive Field 有限：只能获取到局部周围几跳邻居的完整信息。
• 因此，主要的攻击方式应是围绕目标节点周围的小规模黑盒规避攻击。
• 鉴于此，这对欺诈检测模型的要求会显著提升。
• 我们希望建立一个模型，可以同时处理图中大部分的未污染部分和小规模的干扰部分：
  1. 对局部扰动进行抑制很有必要
  2. 同时保证数据足够真实，细节不被大幅修改

B. 标记

图 $G = (V,E)$

• 节点集合 $V$ ，$N_v = |V|$，节点 $v_i$
• 边集合 $E \subset V \times V$ ，边 $e_{ij}$，$N_e = |E|$
• 邻接矩阵 $A \in R^{N_v \times N_v}$，值0或1
• 特征矩阵 $X \in R^{N_v \times N_f}$，节点信息 $x_i$
• 标签 $y_i$ 表示是否为欺诈者0或1，形成 $Y$

在黑盒规避攻击算法中：

• 节点 $v_i$ 的感受野为 $V_{atk}^{i}$，只能知道其中的特征 $X_{atk}^i$、连边 $E_{atk}^i$
• 欺诈节点根据感受野的节点来伪造自己的特征 $x_i$，同时连边到感受野中的一些节点。

规避攻击会在训练阶段之后进行，我们提出的模型目标是：给定一个受攻击的图 $G$，尽可能地降低攻击数据的干扰，完成欺诈节点的正确检测。

C. 攻击算法

考虑到现实情况的复杂性以及欺诈者感受野的有限性，我们采用黑盒规避攻击算法 black-box evasion attack 作为攻击手段：

1. 无法知道模型结构和参数
2. 只能获取自身周围几跳节点的完整信息
3. 可以修改自身的节点特征和连边关系
   这样的攻击算法会更加复杂，但更贴近现实情景。

GNN的基本分类原则就是聚合邻居节点的表征信息（特征、结构）进行图嵌入后进入卷积层进行计算输出达到分类效果。因此，关键在于对图嵌入后的数据进行攻击就能统一特征和结构的攻击。

受图拉普拉斯变换和典型图神经网络GCN的启发，我们将关注节点的卷积层的嵌入 convolutional embeddings $\widetilde{H}$：

$$\widetilde{H} = \widetilde{D}^{-\frac{1}{2}} \widetilde{A} \widetilde{D}^{-\frac{1}{2}}X$$

其中$\widetilde{A}=A+I$表示带有自环的邻接矩阵，$\widetilde{D}$ 是有自环邻接矩阵的度数矩阵。

算法：

1. 选择一个欺诈者节点作为目标节点，设置感受野为3跳。
2. 特征攻击：
   • 选择部分关键特征（在感受野内的 $\widetilde{H_{rec}}$ 使用F-test作为节点选择方法，选出top-5的特征）
   • 计算感受野中的所有节点的这些特征属性的平均值
   • 把平均值加上一点随机小浮动，作为攻击者自己的特征属性
3. 结构攻击：
   • 找到所有2跳上的所有节点（即邻居的邻居，希望模仿邻居的结构）
   • 把其中未连接到攻击者的，连边到攻击者
   • 重新计算 卷积层嵌入 $\widetilde{h_i}$
   • 用 $\widetilde{h_i}$ 去对比 $\widetilde{h_{normal}}$ 和 $\widetilde{h_{fraud}}$
   • 不断迭代，希望这个 $\widetilde{h_i}$ 尽可能接近 normal 的，同时尽可能远离 fraud 的。

D. 模型结构

算法：

1. 首先，增强原始图的结构和特征信息。
2. 节点特征增强：（设计了一个GNN-based generative structure），通过使用平铺的GNN层，所有的节点特征都会被压缩到一个更低维度，增强成为一个更加干净的近似值。
3. 图结构：为每个节点计算某跳内的度数；然后，创建额外的连接（连接哪些？在多跳之内的节点集合中，选出度数top-k的节点，来创建连接）
4. 两两配对形成三种图数据：
   • 增强特征 + 原始结构
   • 原始特征 + 增强结构
   • 原始特征 + 原始结构
     输入GNNs。这样，每一组都是至少保留了部分原始信息的。
5. 通过一个MLP综合信息输出，用于后续分类任务。

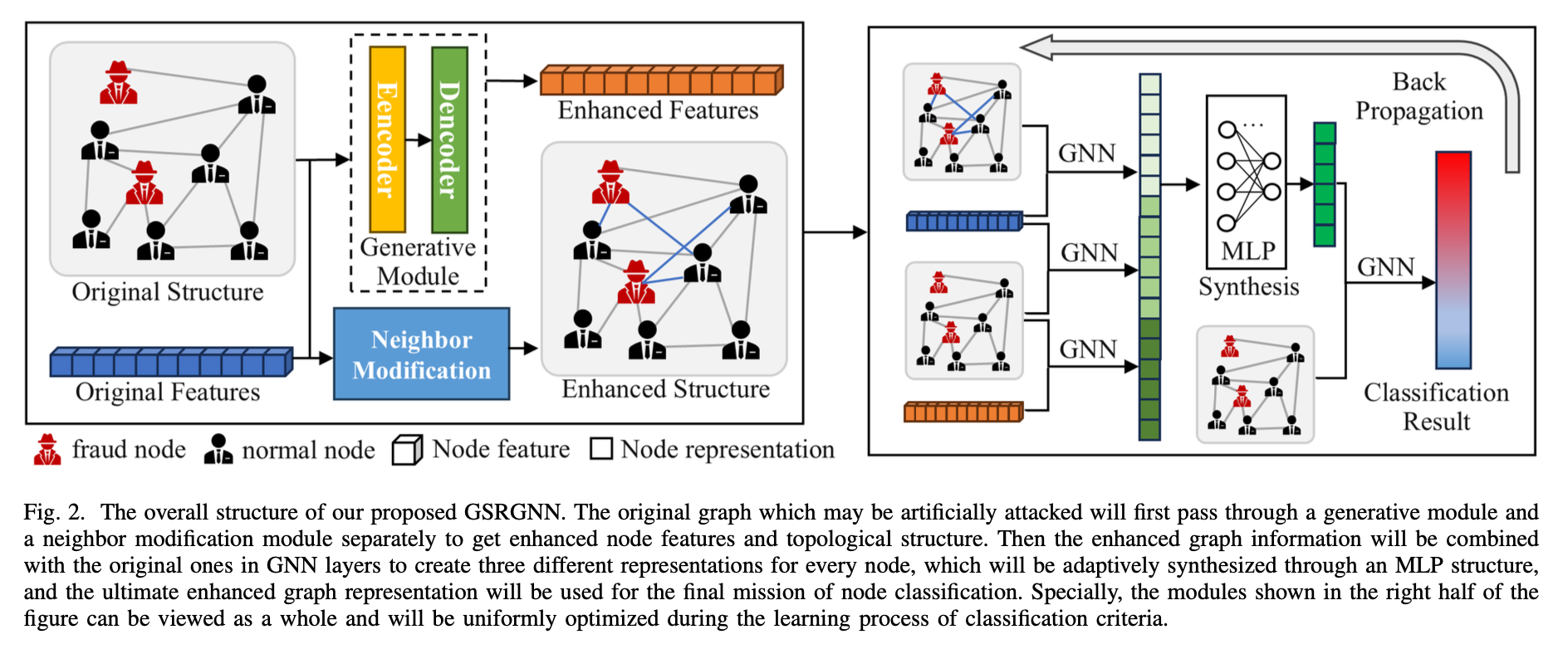
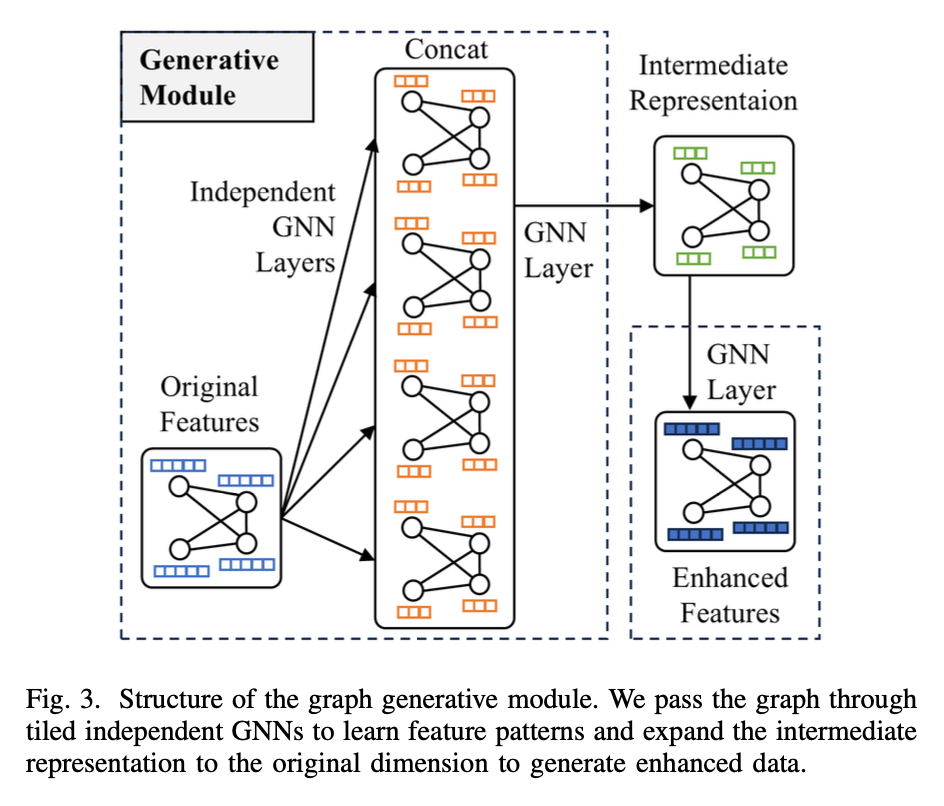
E. 图特征生成模块 Graph Generative Module

使用 Encoder-Decoder 做生成模块，是CV 和 NLP常见手段。

• Encoder：把不同类型的输入序列转换为固定长度的向量。
• Decoder：把压缩向量扩展为某种形式的输出序列。

现有研究主要是关注重建图之间的结构，即邻接矩阵，根据某种规则使用中间生成的向量来进行预测。
本文希望进一步使用节点特征进行增强信息，有以下问题：

1. 计算复杂度高：特征维度包含的信息丰富，且维度远高于邻接矩阵包含的信息。因此生成的中间向量会远复杂，且需要的Decoder也更加复杂。
2. 过度平滑问题：GNN的过度平滑问题限制了GNN的堆叠层数，否则会对节点表示的区分产生负面影响。

整个Encoder 和 Decoder 均是GNN，推荐使用 GraphSAGE 作为 backbone，实验样例显示它能够过滤掉干扰，更加适合本任务。
过程中可以表示为：

$$h_i^{(l)} = \begin{cases} x_i, \quad l=0 \\ ||_{n=1}^{N_h} f_E^n (h_i^{(l-1)}), \quad l = 1 \\ f_E^{N_h +1} (h_i^{(l-1)}), \quad l=2 \\ f_D (h_i^{(h-1)}), \quad l =3 \end{cases}$$

其中 $N_h$ 是第一层的头数，$||$ 为拼接操作。

为了提高信息丰富度，且不触发过平滑问题，在Encoder第一层使用独立参数的多头注意力层，拼接成长向量后，再压缩到低纬度，最后输出到原始维度即可。用余弦相似度保证生成器的有效性：

$$L_{ED} = 1 - cos(x_i, x_i')$$

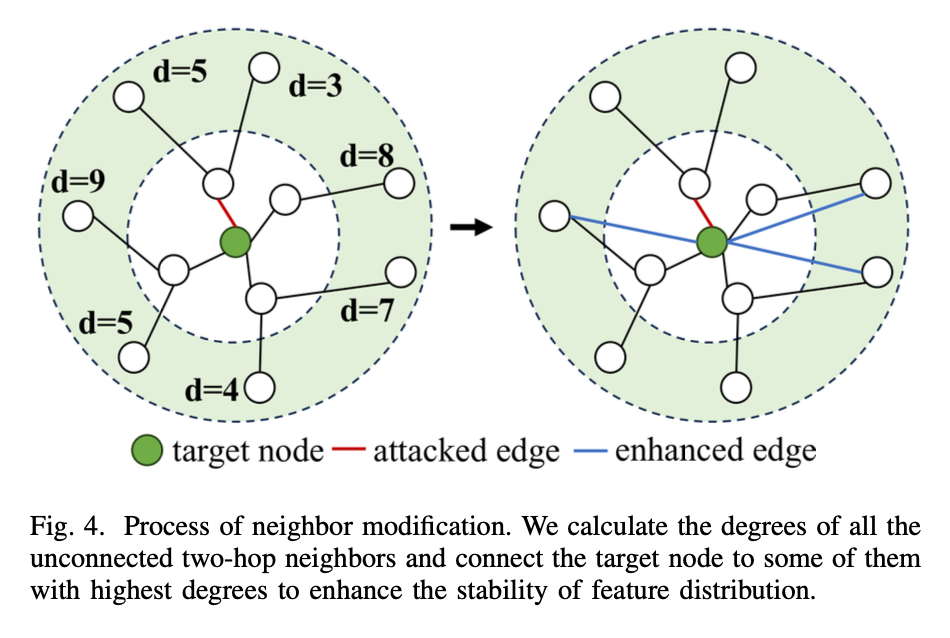
F. 邻居修正 Neighbor Modification

图的拓扑结构同样重要，因此除了图特征生成模块，也需要同时强化图结构。

背景：目前已有的攻击研究基本统一认为，高度数节点是最难以被攻击的，其稳定的图结构提供了足够有效的保障，这也确实符合我们的主观认知，因此一般均认为高度数节点是可信的。
参考论文：【ICLR’2023论文】K. Li, Y. Liu, X. Ao, and Q. He, “Revisiting graph adversarial attack and defense from a data distribution perspective,” in The Eleventh International Conference on Learning Representations, 2023.

1. 首先选择中心节点的2跳以内的所有节点作为候选。
2. 计算节点度数，从大到小排序。
3. 选出其中 top-k 个节点，连边到中心节点。（一般设置k=3）

设计想法如下：

• 对极高度数的节点进行额外连边，并不会对这个节点造成多大的干扰，因为在聚合阶段多一个节点分配的权重在整体中来看是很小。（这也是为什么高度数节点难以被攻击的原因）
• 同时，从整图来看，添加少量边，反而会自适应地弥补了图的缺陷点，因为高稳定节点会给低度数节点带来一部分信息传播。在GNN层中，可以将脆弱节点从可靠的高密度真数据分布聚合而来的嵌入贡献给目标节点，可以帮助稀释虚假信息从而稳定数据。
• 我们选择在两跳内将节点连接到最近的未连接的邻居，这样新连接的高节点可以与目标节点位于相似的数据分布中，并为其提供尽可能有益的信息。

G. 表征合成 Representation Synthesis

并不是直接使用增强信息作为输入，而是选择整体集成。原因如下：

• 虽然原始数据可能有干扰，但是也保存了最原始真实的数据细节，直接丢弃可能损失信息。
• 图特征生成模块和邻居修正不可避免地会带来噪声，且处于理想配置下会显得激进。因此，增强数据应该是作为辅助和补充，而不是代替。
• 此外，得益于原始数据和增强数据的综合思想，我们可以在数据增强模块中创建更大胆的设计，然后使用原始数据自适应地中和它们。

分类过程可以用公式表示为：（两层结构）

$$H^{(1)} = MLP(f_G^1(A',X'), f_G^2(A'',X'), f_G^3(A',X'')) \\ H^{(1)} = f_G^4(H^{(1)})$$

其中的 $f_G$ 是卷积层，可以是任何的GNN，每一个是独立参数。

最后生成的表征，传递给后续分类任务GNN即可。

上述所有GCN和MLP是统一使用随机梯度下降进行参数优化。默认Adam学习率 $1 \times 10^{-3}$，使用交叉熵损失函数度量差距进行优化。

$$L_{cross} = - \sum_{i=1}^{n} ( y_i \log (\hat{y_i}) + (1-y_i) \log (1-\hat(y_i)) )$$