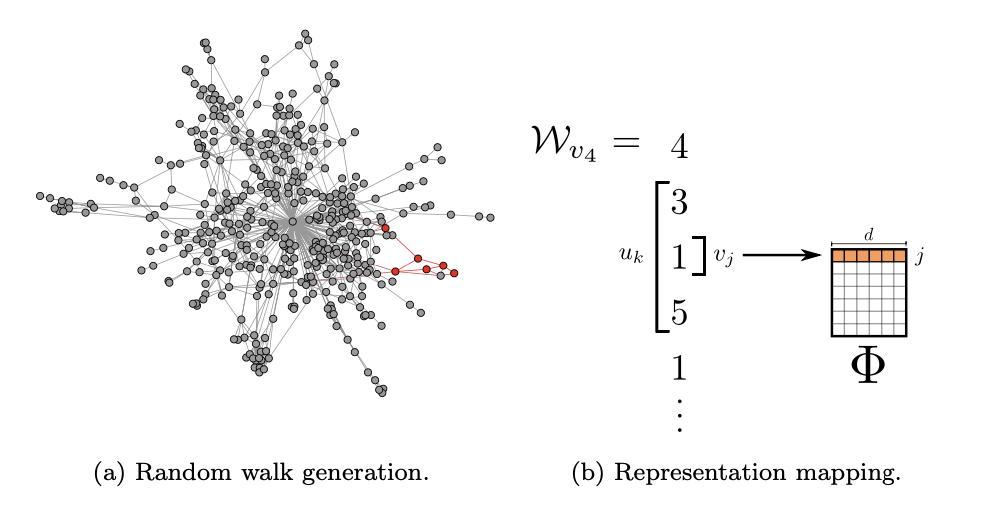
DeepWalk 图嵌入:维基百科词条
DeepWalk 图嵌入:维基百科词条
1. 环境参考
参考资料
https://github.com/prateekjoshi565/DeepWalk
安装工具包
1!pip install networkx gensim pandas numpy tqdm scikit-learn matplotlib
导入工具包
123456789101112131415# 图数据挖掘import networkx as nx# 数据分析import pandas as pdimport numpy as np# 随机数与进度条import randomfrom tqdm import tqdm# 数据可视化import matplotlib.pyplot as plt%matplotlib inline
2. 数据
获取数据
爬虫网站:https://densitydesign.github.io/strumentalia-seealsology/
设置 distance
输入链接:
https://en.wikipedia.org/wiki/Computer_vision
htt ...
ML2021 - HW 5
Homework 5 - Sequence-to-sequence
If you have any questions, feel free to email us at: ntu-ml-2021spring-ta@googlegroups.com
(4/21 Updates)
Link to reference training curves.
(4/14 Updates)
Link to tutorial video part 1 part 2.
Now defaults to load "avg_last_5_checkpoint.pt" to generate prediction.
Expected run time on Colab with Tesla T4
Baseline
Details
Total Time
Simple
2m 15s $\times$30 epochs
1hr 8m
Medium
4m $\times$30 epochs
2hr
Strong
8m $\times$30 epochs (backwa ...
ML2021 - HW 4
HW4: Speaker Prediction
goal: learn to use transformer
赛事:https://www.kaggle.com/competitions/ml2021spring-hw4/overview
Baselines:
Easy: Run sample code and know how to use transformer.
Medium: Know how to adjust parameters of transformer.
Hard: Construct conformer which is a variety of transformer.
Other links
Kaggle: link
Slide: link
Data: link
Video (Chinese): link
Video (English): link
Solution for downloading dataset fail.: link
1. Data
Dataset
12345678910111213141516171819202 ...
ML2021 - HW 3
HW3 : Convolutional Nueral Network
In this homework, you are required to build a convolutional neural network for image classification, possibly with some advanced training tips.
There are three levels here:
Easy: Build a simple convolutional neural network as the baseline. (2 pts)
Medium: Design a better architecture or adopt different data augmentations to improve the performance. (2 pts)
Hard: Utilize provided unlabeled data to obtain better results. (2 pts)
https://www.kaggle.com/competitio ...
ML2021 - HW 2
HW2: Phoneme Classification
Platform : Kaggle
Sample Code : Google Colab
0. Prepare
TIMIT
This homework is a multiclass classification task, we are going to train a deep neural network classifier to predict the phonemes for each frame from the speech corpus TIMIT.
Google Colab 下载:(或官网下载也行)
123!gdown --id '1HPkcmQmFGu-3OknddKIa5dNDsR05lIQR' --output data.zip!unzip data.zip!ls
zsh:1: command not found: gdown
unzip: cannot find or open data.zip, data.zip.zip or data.zip.ZIP.
HW02.pdf ...
ML2021 - HW 1
HW1: COVID-19 Cases Prediction (Regression)
Platform : Kaggle
Sample Code : Google Colab
Objectives:
Solve a regression problem with deep neural network. (DNN)
Understand basic DNN training tips.
Get familiar with PyTorch.
0. Prepare
12import warningswarnings.filterwarnings('ignore')
预览数据
12tr_path = 'input/covid.train.csv'tt_path = 'input/covid.test.csv'
123456# 预览数据import pandas as pddata = pd.read_csv(tr_path)print("Shape:",data.shape)data.iloc[:,4 ...
INTRO to DL - Kaggle 官方课程
来源:Kaggle 官方课程 Intro to Deep Learning
2024-09-01@isSeymour
Intro to Deep Learning
Exercise: Binary Classification
1.导入数据
123456789101112import pandas as pdimport matplotlib.pyplot as pltfrom sklearn.model_selection import train_test_splitfrom sklearn.preprocessing import StandardScaler, OneHotEncoderfrom sklearn.impute import SimpleImputerfrom sklearn.pipeline import make_pipelinefrom sklearn.compose import make_column_transformerhotel = pd.read_csv('../input/hotel.csv')print(" ...
Data Visualization - Kaggle 官方课程
来源:Kaggle 官方课程 Data Visualization
2024-09-01@isSeymour
Data Visualization
总览:
展现内容:
Trends 趋势
代码
功能
lineplot 折线图
用于展示数据随时间或其他连续变量的变化趋势
Relationship 关系
代码
功能
barplot 柱状图
用于展示不同类别或分组数据的数量或频率
heatmap 热图
用于显示数据的密度或强度,通过颜色的深浅来表示数值的大小
scatterplot 散点图
用于展示两个变量之间关系
swarmplot 蜂群图
用于显示数据分布的可视化图表,通过将数据点以散点的方式展示在类别上,并避免数据点重叠。它适用于展示单变量或多变量的离散数据分布,特别是当数据量较小或希望看到每个数据点的具体位置时
regplot 回归图
用于展示回归分析结果的数据可视化工具。它通常包括一个散点图和一条回归线,帮助直观地展示两个变量之间的关系及其回归模型的拟合效果
lmplot 线性回归图
用于展示线性回归分析结果的 ...
Intermediate ML - Kaggle 官方课程
来源:Kaggle 官方课程 | Intermediate Machine Learning
2024-08-31@isSeymour
Intermediate Machine Learning
1. Missing Value 缺失值
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566import pandas as pdfrom sklearn.model_selection import train_test_splitfrom sklearn.ensemble import RandomForestRegressorfrom sklearn.metrics import mean_absolute_errorfrom sklearn.impute import SimpleImputer# 数据准备X_full = pd.read_csv('../input/train. ...
Pandas - Kaggle 官方课程
来源:Kaggle 官方课程 Pandas
2024-08-30@isSeymour
Pandas - Kaggle
1. Creating, Reading and Writing
12import pandas as pdpd.set_option('display.max_rows', 5)
123fruits = pd.DataFrame({'Apples': [30], 'Bananas': [21]})fruits
.dataframe tbody tr th:only-of-type {
vertical-align: middle;
}
.dataframe tbody tr th {
vertical-align: top;
}
.dataframe thead th {
text-align: right;
}
...